机器学习分类问题（交叉熵、不均衡样本训练时的损失函数系数等），复习一下。

先看二分类问题。

目标算法：输入一张胸部X光照片，判断其是否有病。即：输出有病的概率。Y=1作为有病标记，Y=0作为没病标记

即：算法给出的是P(Y=1|X)，也就是输出一个图片X，计算它有病的概率。

如何训练：

样本1(Ex1),是一张有病的胸部照片，初始算法给出的答案是0.2（明显偏小），即P(Y=1|Ex1)=0.2, 损失函数为L(X,y) = -log P(Y=1|X) = -log0.2

样本2(Ex2),是一张没病的胸部照片，初始算法给出的答案是0.7（明显偏大），即P(Y=1|Ex2)=0.7, 那么P(Y=0|Ex2)=1 - P(Y=1|Ex2) = 0.3  

损失函数为L(X,y) = -log P(Y=0|X) = -log0.3

这种损失算法叫做交叉熵。

其实就是给概率（概率是0-1之间）外面套个-log函数，概率与真实标签接近的时候（比如有个有病的照片，P(Y=1|X)应该接近1，那么损失函数就应该接近0，如果P(Y=1|X)接近0，那就说明算错了，代价需要付出很大，所以损失函数应该很大——接近0的话损失函数就是无穷大）

（再比如有个正常人没病的照片，那么P(Y=0|X)应该接近1，损失函数就应该接近0，反之。）

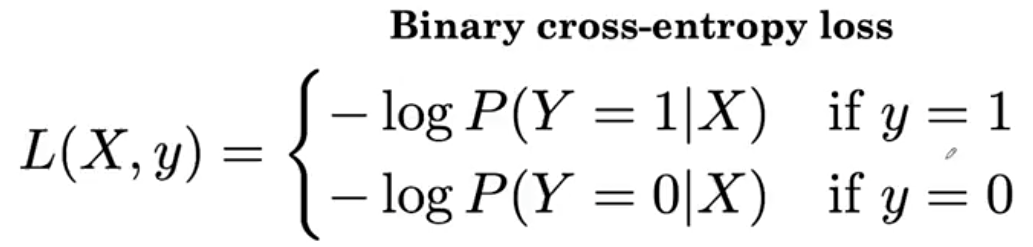
继续看样本不均匀时候，如何优化训练：

把有病的样本叫做正例Positive，没病的样本叫做负例Negative。

现实中，没病的人多，有病的人少。导致训练数据里负例多，正例少。导致负例算出来的损失函数贡献多。

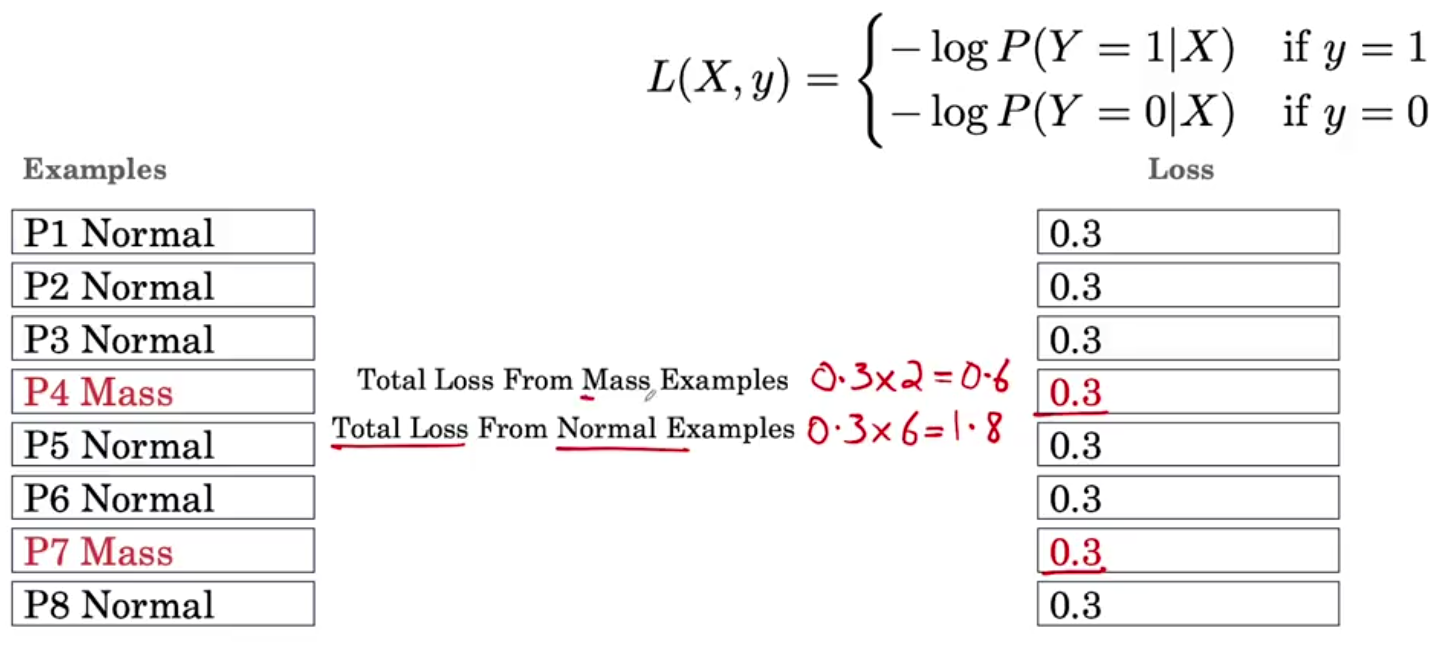
 最直观的方式是给损失函数加个权重。

 

权重是如何计算的？比如，8个样本里面，6个没病是负例，2个有病是正例。

正例样本的损失函数的系数（正例数量本来就少，损失贡献少，所以需要用权重来提升）

负例样本的损失函数的系数（负例数量本来就多，损失贡献多，所以需要用权重来降低）

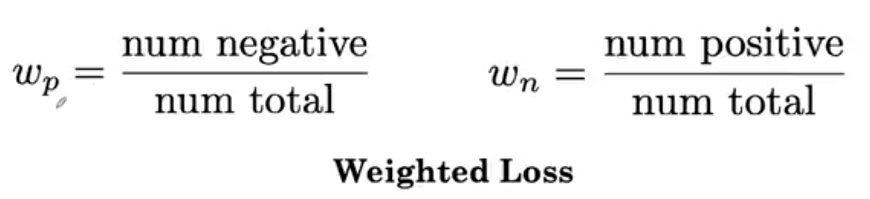
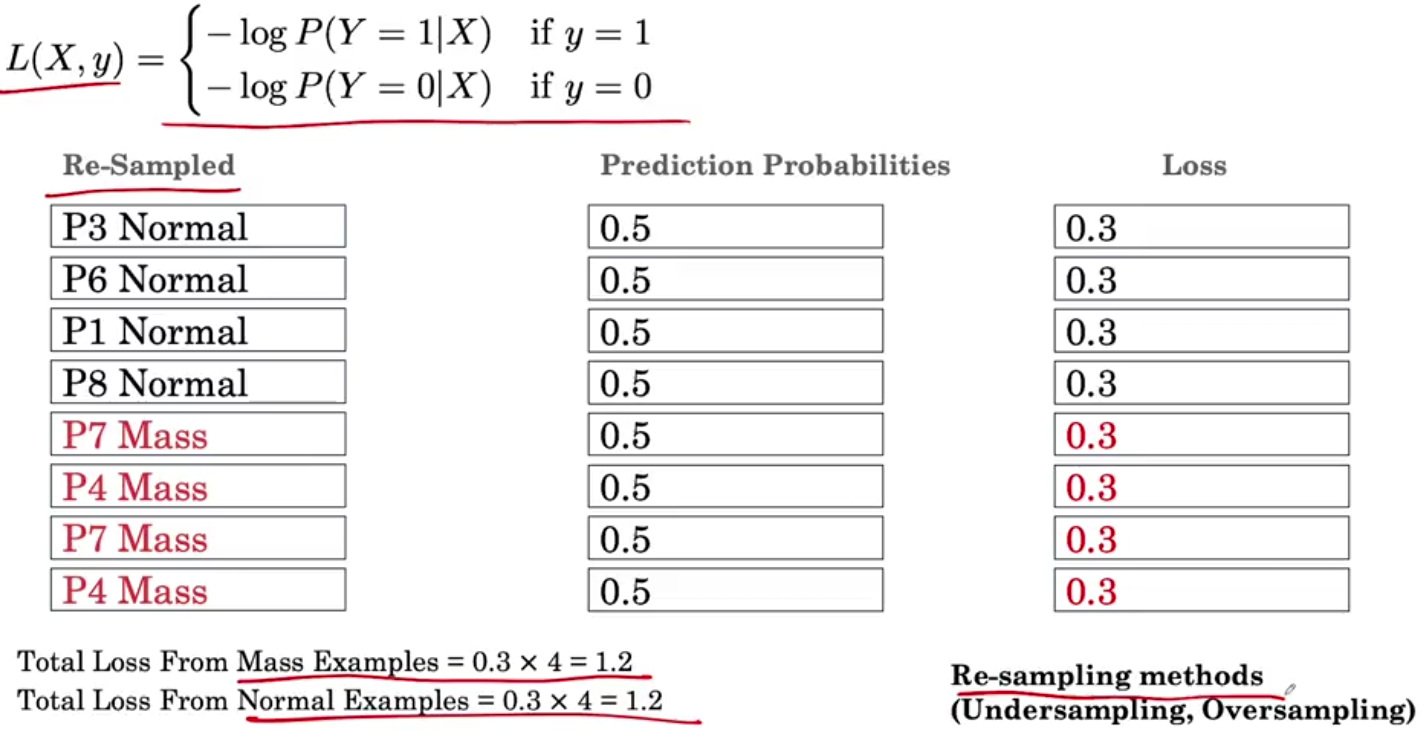
如果不想引入损失函数的权重系数，还可以通过重新采样样本集，重新制作训练数据集的方法来实现。

比如因为负例（没病的人）太多，可以从里面随机选4个。

正例（有病的人）太少，可以把正例样本重复使用。最终正例负例数量一样，损失函数贡献一样。