CSAPP DataLab

DataLab 就是看题两分钟，一题半小时的那种，非常考验脑子，我也是在参考很多很多方案之后才完成，记录一下，如果想快速地学会这些题目，还是自己想 -> 看大佬代码 -> 理解大佬代码，这样比较有益。

以下是给予我帮助的博主文章，感谢这些优秀同学无偿的分享：

• https://wdxtub.com/csapp/thick-csapp-lab-1/2016/04/16/
• https://www.acwing.com/blog/content/29748/
• https://www.cnblogs.com/kangyupl/p/13022465.html
• https://blog.csdn.net/qq_43508844/article/details/121178871

这是我最终的 lab1 成绩，其中最后一个测试是因为我的虚拟机性能孱弱导致超时，代码并无问题。

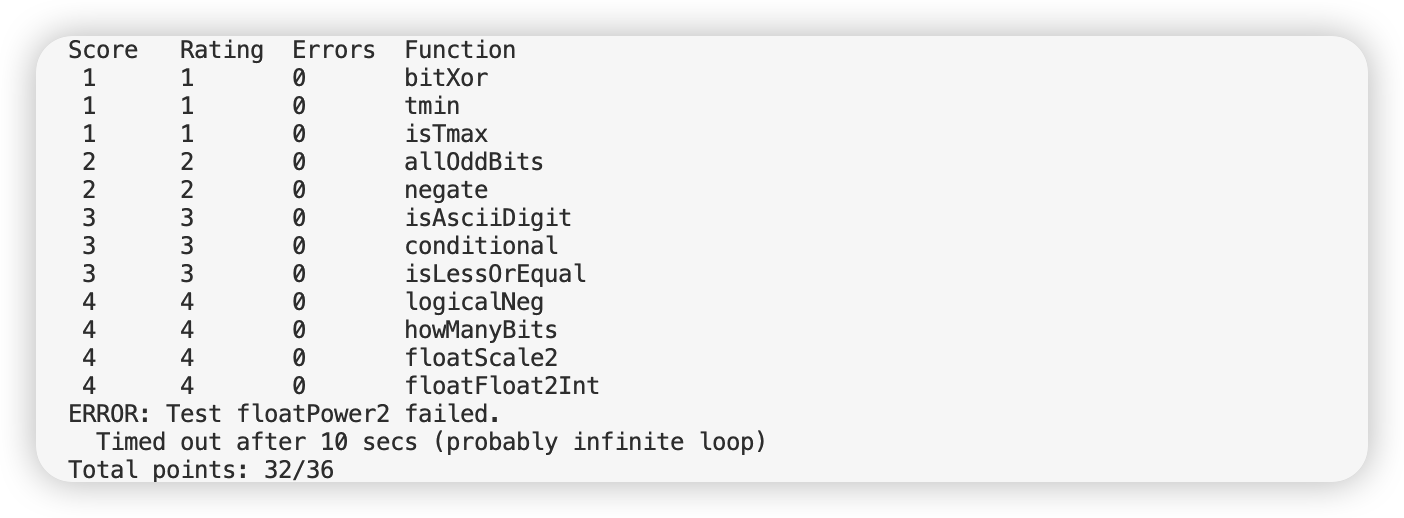
记录一下每个题目的思路

1. bitXor, 异或运算, 需要解析异或为 (a & ~b) | (~a & b), 然后用德摩根律将 | 转化为 &;
2. tmin, 判断 tmin, tmin 是一个特殊的值, 它是二进制补码中符号位为1但是其余其它位置为 0 的数;
3. isTmax, tmax = \(2^n - 1\), 因此 tmax + tmax + 2 = 0, 同样有此性质的还有 0xFFFFFFFF, 再排除掉它即可;
4. allOddBits, 即判断是否是0xAAAAAAAA, 由于不让构造这么大的字面值, 可以用左移和相加获得, 用它来提取出 x 的奇数位置, 然后再与0xAAAAAAAA比较;
5. negate, 取相反数, 取反加一即可, tmin 的相反数还是 tmin;
6. isAsciiDigit, 0x39 - x 和 x - 0x30 需要同为正;
7. conditional, 要构造一个 x 的操作使其只有0xFFFFFFFF和0x00000000这两种值, 因此考虑到 !~x + 1;
8. isLessOrEqual, 分同号和不同号，不同号判断 x 为负 y 为正, 同号判断 y - x 的符号;
9. logicalNeg, 取 x > 0 和 x < 0 的符号, x > 0 时可以用先取反再判断的方式(~x + 1) >> 31 & 1, 最后判断它是否为 0, 与 1 异或可得结果;
10. howManyBits, 正数不变, 负数取反, 然后判断绝对值, 先右移 16 位判断一下高 16 位是否为 0,
    10.1 如果不为 0 那么右移 16 位，对高 16 位判断它的高 8 位...
    10.2 如果为 0, 那么不右移, 判断它的 16 - 24(右移 8 位)是否为 0 ...
    10.3 类似二分的做法
11. floatScale2, 先取到 sign, exp, frac（保持 32 位）, 然后根据 exp 判断是否为规格化数, 然后根据 exp 是 0 or 非0 来判断对 frac << 1还是 exp + 1;
12. floatFloat2Int, 先取到 sign, exp, frac, 然后把隐含的 1 补充上, 接着判断 exp 的值是否是题目中指出的特殊值, 最后做相应的移动;
13. float2Power, 对 x + 127 也就是 exp 做完判断移动即可;

点击查看代码

/*
 * CS:APP Data Lab
 *
 * <Please put your name and userid here>
 * Name: immelon
 *
 * bits.c - Source file with your solutions to the Lab.
 *          This is the file you will hand in to your instructor.
 *
 * WARNING: Do not include the <stdio.h> header; it confuses the dlc
 * compiler. You can still use printf for debugging without including
 * <stdio.h>, although you might get a compiler warning. In general,
 * it's not good practice to ignore compiler warnings, but in this
 * case it's OK.
 */

#if 0
/*
 * Instructions to Students:
 *
 * STEP 1: Read the following instructions carefully.
 */

You will provide your solution to the Data Lab by
editing the collection of functions in this source file.

INTEGER CODING RULES:
 
  Replace the "return" statement in each function with one
  or more lines of C code that implements the function. Your code 
  must conform to the following style:
 
  int Funct(arg1, arg2, ...) {
      /* brief description of how your implementation works */
      int var1 = Expr1;
      ...
      int varM = ExprM;

      varJ = ExprJ;
      ...
      varN = ExprN;
      return ExprR;
  }

  Each "Expr" is an expression using ONLY the following:
  1. Integer constants 0 through 255 (0xFF), inclusive. You are
      not allowed to use big constants such as 0xffffffff.
  2. Function arguments and local variables (no global variables).
  3. Unary integer operations ! ~
  4. Binary integer operations & ^ | + << >>
    
  Some of the problems restrict the set of allowed operators even further.
  Each "Expr" may consist of multiple operators. You are not restricted to
  one operator per line.

  You are expressly forbidden to:
  1. Use any control constructs such as if, do, while, for, switch, etc.
  2. Define or use any macros.
  3. Define any additional functions in this file.
  4. Call any functions.
  5. Use any other operations, such as &&, ||, -, or ?:
  6. Use any form of casting.
  7. Use any data type other than int.  This implies that you
     cannot use arrays, structs, or unions.

 
  You may assume that your machine:
  1. Uses 2s complement, 32-bit representations of integers.
  2. Performs right shifts arithmetically.
  3. Has unpredictable behavior when shifting if the shift amount
     is less than 0 or greater than 31.


EXAMPLES OF ACCEPTABLE CODING STYLE:
  /*
   * pow2plus1 - returns 2^x + 1, where 0 <= x <= 31
   */
  int pow2plus1(int x) {
     /* exploit ability of shifts to compute powers of 2 */
     return (1 << x) + 1;
  }

  /*
   * pow2plus4 - returns 2^x + 4, where 0 <= x <= 31
   */
  int pow2plus4(int x) {
     /* exploit ability of shifts to compute powers of 2 */
     int result = (1 << x);
     result += 4;
     return result;
  }

FLOATING POINT CODING RULES

For the problems that require you to implement floating-point operations,
the coding rules are less strict.  You are allowed to use looping and
conditional control.  You are allowed to use both ints and unsigneds.
You can use arbitrary integer and unsigned constants. You can use any arithmetic,
logical, or comparison operations on int or unsigned data.

You are expressly forbidden to:
  1. Define or use any macros.
  2. Define any additional functions in this file.
  3. Call any functions.
  4. Use any form of casting.
  5. Use any data type other than int or unsigned.  This means that you
     cannot use arrays, structs, or unions.
  6. Use any floating point data types, operations, or constants.


NOTES:
  1. Use the dlc (data lab checker) compiler (described in the handout) to 
     check the legality of your solutions.
  2. Each function has a maximum number of operations (integer, logical,
     or comparison) that you are allowed to use for your implementation
     of the function.  The max operator count is checked by dlc.
     Note that assignment ('=') is not counted; you may use as many of
     these as you want without penalty.
  3. Use the btest test harness to check your functions for correctness.
  4. Use the BDD checker to formally verify your functions
  5. The maximum number of ops for each function is given in the
     header comment for each function. If there are any inconsistencies 
     between the maximum ops in the writeup and in this file, consider
     this file the authoritative source.

/*
 * STEP 2: Modify the following functions according the coding rules.
 * 
 *   IMPORTANT. TO AVOID GRADING SURPRISES:
 *   1. Use the dlc compiler to check that your solutions conform
 *      to the coding rules.
 *   2. Use the BDD checker to formally verify that your solutions produce 
 *      the correct answers.
 */

#endif
// 1
/*
 * bitXor - x^y using only ~ and &
 *   Example: bitXor(4, 5) = 1
 *   Legal ops: ~ &
 *   Max ops: 14
 *   Rating: 1
 */
int bitXor(int x, int y)
{
  /*
   * ~(a | b) = ~a & ~b
   * a ^ b = (~a & b) | (a & ~b)
   */
  return ~(~(~x & y) & (~(x & ~y)));
}
/*
 * tmin - return minimum two's complement integer
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 4
 *   Rating: 1
 */
int tmin(void)
{
  return 1 << 31;
}
// 2
/*
 * isTmax - returns 1 if x is the maximum, two's complement number,
 *     and 0 otherwise
 *   Legal ops: ! ~ & ^ | +
 *   Max ops: 10
 *   Rating: 1
 */
int isTmax(int x)
{
  return !((x + x + 2) ^ (!~x));
}
/*
 * allOddBits - return 1 if all odd-numbered bits in word set to 1
 *   where bits are numbered from 0 (least significant) to 31 (most significant)
 *   Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 2
 */
int allOddBits(int x)
{
  int y = (0xAA << 24) + (0xAA << 16) + (0xAA << 8) + 0xAA;
  return !(~(y & x) & y);
}
/*
 * negate - return -x
 *   Example: negate(1) = -1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 5
 *   Rating: 2
 */
int negate(int x)
{
  // 整体取反 + 1
  return ~x + 1;
}
// 3
/*
 * isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')
 *   Example: isAsciiDigit(0x35) = 1.
 *            isAsciiDigit(0x3a) = 0.
 *            isAsciiDigit(0x05) = 0.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 15
 *   Rating: 3
 */
int isAsciiDigit(int x)
{
  int a = 0x39 + (~x + 1);
  int b = x + (~0x30 + 1);
  // 两个差均为正才返回 1
  return !((a | b) & (1 << 31));
}
/*
 * conditional - same as x ? y : z
 *   Example: conditional(2,4,5) = 4
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 16
 *   Rating: 3
 */
int conditional(int x, int y, int z)
{
  int mask = ~!x + 1;
  return (y & ~mask) | (z & mask);
}
/*
 * isLessOrEqual - if x <= y  then return 1, else return 0
 *   Example: isLessOrEqual(4,5) = 1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 24
 *   Rating: 3
 */
int isLessOrEqual(int x, int y)
{
  // Boolean value indicating sign of x
  // 1 = Negative
  // 0 = Non-Negative
  int sign_x = x >> 31;

  // Boolean value indicating sign of y
  // 1 = Negative
  // 0 = Non-Negative
  int sign_y = y >> 31;

  // if the signs are equal, then
  // if x is larger, sign bit of (~y + x) is 0
  // if y is larger or equal to x, sign bit of (~y + x) is 1
  // (y - x) >= 0  <=> !((y + (~x + 1)) >> 31)
  int equal = !(sign_x ^ sign_y) & !((y + (~x + 1)) >> 31);

  // if signs are not equal, these principles are reversed.
  int notEqual = sign_x & !sign_y;

  // this | returns 0 when it is x is greater, so you have to negate it.
  return equal | notEqual;
}
// 4
/*
 * logicalNeg - implement the ! operator, using all of
 *              the legal operators except !
 *   Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
 *   Legal ops: ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 4
 */
int logicalNeg(int x)
{
  // x < 0
  int neg = x >> 31 & 1;
  // x > 0(except tmin)
  int pos = (~x + 1) >> 31 & 1;
  // x != 0
  int notZero = neg | pos;
  return notZero ^ 1;
}
/* howManyBits - return the minimum number of bits required to represent x in
 *             two's complement
 *  Examples: howManyBits(12) = 5
 *            howManyBits(298) = 10
 *            howManyBits(-5) = 4
 *            howManyBits(0)  = 1
 *            howManyBits(-1) = 1
 *            howManyBits(0x80000000) = 32
 *  Legal ops: ! ~ & ^ | + << >>
 *  Max ops: 90
 *  Rating: 4
 */
int howManyBits(int x)
{
  // 正数不变，负数取反
  int temp = x ^ (x >> 31);
  // 0 只需要一位来表示，正数和负数至少需要两位
  int isZero = !temp;
  // temp 不为 0 时，notZeroMask = 0xffffffff
  int notZeroMask = (!(!temp) << 31) >> 31;
  int bit_16, bit_8, bit_4, bit_2, bit_1;

  // temp 右移 16 位，剩余最高的 16 位，最高的 16 为如果不为 0，则 bit_16 = 16;
  bit_16 = !(!(temp >> 16)) << 4;
  temp = temp >> bit_16;

  bit_8 = !(!(temp >> 8)) << 3;
  temp = temp >> bit_8;

  bit_4 = !(!(temp >> 4)) << 2;
  temp = temp >> bit_4;

  bit_2 = !(!(temp >> 2)) << 1;
  temp = temp >> bit_2;

  bit_1 = !(!(temp >> 1));

  // + 2 中一位是符号位，另一位是值
  temp = bit_16 + bit_8 + bit_4 + bit_2 + bit_1 + 2;

  return isZero | (temp & notZeroMask);
}
// float
/*
 * floatScale2 - Return bit-level equivalent of expression 2*f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representation of
 *   single-precision floating point values.
 *   When argument is NaN, return argument
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned floatScale2(unsigned uf)
{
  unsigned s = (uf >> 31) << 31;
  unsigned exp = (uf << 1) >> 24;
  unsigned frac = (uf << 9) >> 9;

  if (exp == 0xff)
    return uf;
  if (exp == 0)
    frac = frac << 1;
  else
    exp = exp + 1;

  return s | (exp << 23) | frac;
}
/*
 * floatFloat2Int - Return bit-level equivalent of expression (int) f
 *   for floating point argument f.
 *   Argument is passed as unsigned int, but
 *   it is to be interpreted as the bit-level representation of a
 *   single-precision floating point value.
 *   Anything out of range (including NaN and infinity) should return
 *   0x80000000u.
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
int floatFloat2Int(unsigned uf)
{
  int exp = (uf >> 23) & 0xFF;
  int frac = uf & 0x007fffff;
  int sign = uf & 0x80000000;
  int bias = exp - 127;

  if (exp == 255 || bias > 30)
    return 0x80000000u;
  else if (!exp || bias < 0)
    return 0;

  frac = frac | 0x00800000;

  if (bias > 23)
    frac = frac << (bias - 23);
  else
    frac = frac >> (23 - bias);

  if (sign)
    return ~(frac) + 1;
  return frac;
}
/*
 * floatPower2 - Return bit-level equivalent of the expression 2.0^x
 *   (2.0 raised to the power x) for any 32-bit integer x.
 *
 *   The unsigned value that is returned should have the identical bit
 *   representation as the single-precision floating-point number 2.0^x.
 *   If the result is too small to be represented as a denorm, return
 *   0. If too large, return +INF.
 *
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned floatPower2(int x)
{
  // exp is the unsigned number in exp area of float.
  x = x + 127;
  // the x of 2.0^x is too small(x < -127, exp < 0).
  if (x <= 0) return 0;
  // the x of 2.0^x is too large(x >= 127, exp >= 255)
  if (x >= 255) return 0x7f800000;
  return x << 23;
}