xgboost
0、xgboost 背景
XGBoost [1]是一个开源 软件库,它为C ++,Java, Python,[2] R,[3]和 Julia提供了梯度提升框架。[4] 它适用于Linux, Windows,[5]和 macOS。[6]从项目描述中,它旨在提供“可扩展,可移植和分布式梯度提升(GBM,GBRT,GBDT)库”。除了在单个机器上运行外,它还支持分布式处理框架 Apache Hadoop,Apache Spark和Apache Flink。作为许多机器学习竞赛获胜团队的首选算法,它最近获得了很多人气和关注。【1】(https://en.wikipedia.org/wiki/XGBoost)
1、基础知识梳理
1.1、熵
1.2、泰勒展开
2、知识铺垫
2.1、决策树
2.2、回归树与集成学习
3、xgboost 原理
3.1 xgboost 目标函数
3.2 xgboost 公式推导
3.3 xgboost 参数调优
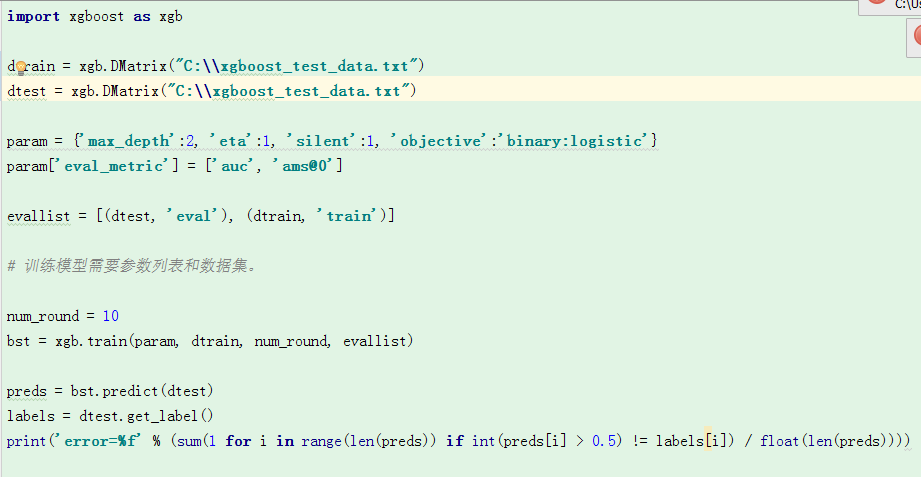
4、xgboost 代码实现
1、基础知识梳理
1.1、熵
1.1.1 什么是熵 - Entropy
词源 - 最初来源于热力学
Entropy来源于希腊语,原意:内向,即:一个系统不受外部干扰时往内部稳定状态发展的特性。定义的其实是一个热力学的系统变化的趋势
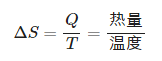
1923年,德国科学家普朗克来中国讲学用到entropy这个词,胡刚复教授看到这个公式,创造了“熵”字,因为“火”和热量有关,定义式又是热量比温度,相当自洽。
信息论
信息论中,熵是接受的每条消息中包含的信息的平均值。又被称为信息熵、信源熵、平均自信息量。可以被理解为不确定性的度量,熵越大,信源的分布越随机
1948年,由克劳德·爱尔伍德·香农将热力学中的熵引入信息论,所以也叫做:香农熵
生态学
在生态学中,熵表示生物多样性的指标
广义的定义
熵是描述一个系统的无序程度的变量;同样的表述还有,熵是系统混乱度的度量,一切自发的不可逆过程都是从有序到无序的变化过程,向熵增的方向进行
我们接下来要讨论的信息熵 交叉熵 相对熵 更多的着眼于信息论的角度,换句话说,更加关注概率和不确定性。
1.1.2 详解机器学习中的熵、条件熵、相对熵和交叉熵
信息熵 (information entropy)(https://www.cnblogs.com/kyrieng/p/8694705.html)
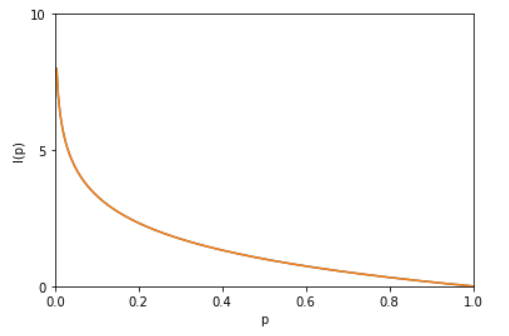
信息熵也就是上面提到的香农熵。下面详解 一下信息熵。一条信息的信息量大小和它的不确定性有直接的关系。我们需要搞清楚一件非常非常不确定的事,或者是我们一无所知的事,就需要了解大量的信息。相反,如果我们对某件事已经有了较多的了解,我们就不需要太多的信息就能把它搞清楚。所以,从这个角度,我们可以认为,信息量的度量就等于不确定性的多少。比如,有人说广东下雪了。对于这句话,我们是十分不确定的。因为广东几十年来下雪的次数寥寥无几。为了搞清楚,我们就要去看天气预报,新闻,询问在广东的朋友,而这就需要大量的信息,信息熵很高。再比如,中国男足进军2022年卡塔尔世界杯决赛圈。对于这句话,因为确定性很高,几乎不需要引入信息,信息熵很低。考虑一个离散的随机变量 x,由上面两个例子可知,信息的量度应该依赖于概率分布 p(x),因此我们想要寻找一个函数 I(x),它是概率 p(x) 的单调函数,表达了信息的内容。怎么寻找呢?如果我们有两个不相关的事件 x 和 y,那么观察两个事件同时发生时获得的信息量应该等于观察到事件各自发生时获得的信息之和,即:I(x,y)=I(x)+I(y)。因为两个事件是独立不相关的,因此 p(x,y)=p(x)p(y)。根据这两个关系,很容易看出 I(x)一定与 p(x) 的对数有关 (因为对数的运算法则是 loga(mn)=logam+logan)。因此,我们有I(x)=−logp(x)
其中负号是用来保证信息量是正数或者零。而 log函数基的选择是任意的(信息论中基常常选择为2,因此信息的单位为比特bits;而机器学习中基常常选择为自然常数,因此单位常常被称为奈特nats)。I(x) 也被称为随机变量 x 的自信息 (self-information),描述的是随机变量的某个事件发生所带来的信息量。图像如图:
最后,我们正式引出信息熵。 现在假设一个发送者想传送一个随机变量的值给接收者。那么在这个过程中,他们传输的平均信息量可以通过求 I(x)=−logp(x) 关于概率分布 p(x) 的期望得到,即:
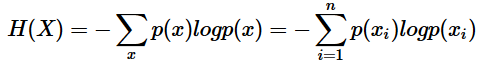
H(X) 就被称为随机变量 x 的熵,它是表示随机变量不确定的度量,是对所有可能发生的事件产生的信息量的期望。
从公式可得,随机变量的取值个数越多,状态数也就越多,信息熵就越大,混乱程度就越大。当随机分布为均匀分布时,熵最大,且 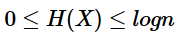
。稍后证明。将一维随机变量分布推广到多维随机变量分布,则其联合熵 (Joint entropy) 为:
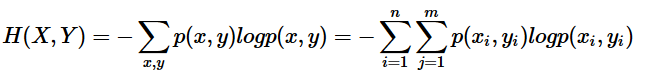
注意点:
1、熵只依赖于随机变量的分布,与随机变量取值无关,所以也可以将 X的熵记作 H(p)。
2、令0log0=0(因为某个取值概率可能为0)。
那么这些定义有着什么样的性质呢?考虑一个随机变量 x
。这个随机变量有4种可能的状态,每个状态都是等可能的。为了把 x 的值传给接收者,我们需要传输2比特的消息。![]()
现在考虑一个具有4种可能的状态 {a,b,c,d}
的随机变量,每个状态各自的概率为 ![]()
这种情形下的熵为:
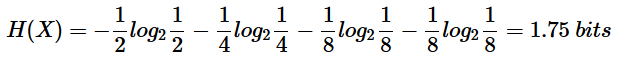
我们可以看到,非均匀分布比均匀分布的熵要小。现在让我们考虑如何把变量状态的类别传递给接收者。与之前一样,我们可以使用一个2比特的数字来完成这件事情。然而,我们可以利用非均匀分布这个特点,使用更短的编码来描述更可能的事件,使用更长的编码来描述不太可能的事件。我们希望这样做能够得到一个更短的平均编码长度。我们可以使用下面的编码串(哈夫曼编码):0、10、110、111来表示状态 {a,b,c,d}
。传输的编码的平均长度就是:
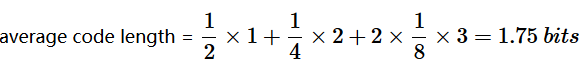
这个值与上方的随机变量的熵相等。熵和最短编码长度的这种关系是一种普遍的情形。Shannon 编码定理https://baike.baidu.com/item/Shannon%20%E7%BC%96%E7%A0%81%E5%AE%9A%E7%90%86/15585931?fr=aladdin 表明熵是传输一个随机变量状态值所需的比特位下界(最短平均编码长度)。因此,信息熵可以应用在数据压缩方面。这里这篇文章http://www.ruanyifeng.com/blog/2014/09/information-entropy.html讲的很详细了,我就不赘述了。
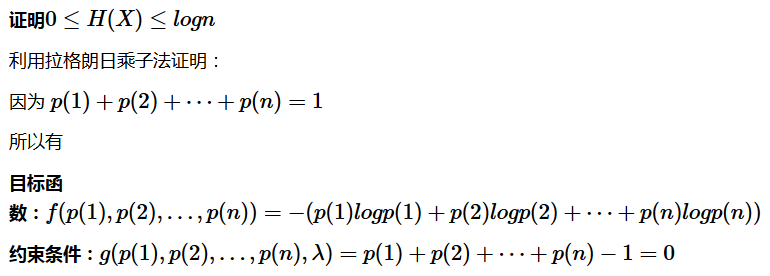

注:极大值极小值条件(这里没有提及)
条件熵 (Conditional entropy)
条件熵 H(Y|X)
表示在已知随机变量 X 的条件下随机变量 Y 的不确定性。条件熵 H(Y|X) 定义为 X 给定条件下 Y 的条件概率分布的熵对 X
的数学期望:
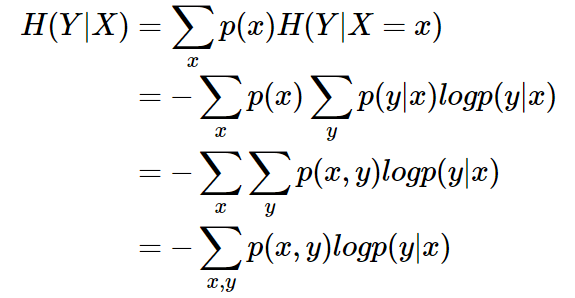
条件熵 H(Y|X)相当于联合熵 H(X,Y) 减去单独的熵 H(X),即H(Y|X)=H(X,Y)−H(X),证明如下:
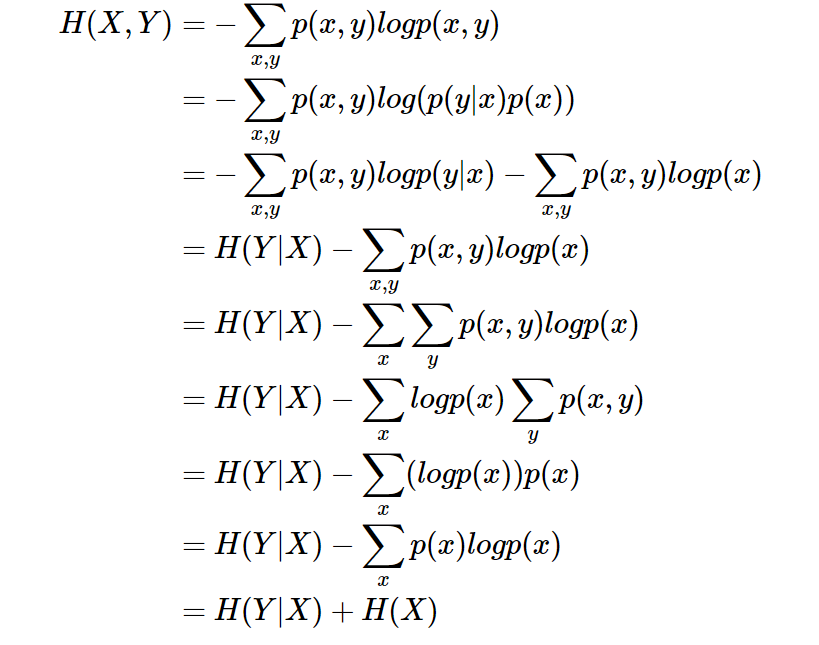
举个例子,比如环境温度是低还是高,和我穿短袖还是外套这两个事件可以组成联合概率分布 H(X,Y),因为两个事件加起来的信息量肯定是大于单一事件的信息量的。假设 H(X) 对应着今天环境温度的信息量,由于今天环境温度和今天我穿什么衣服这两个事件并不是独立分布的,所以在已知今天环境温度的情况下,我穿什么衣服的信息量或者说不确定性是被减少了。当已知 H(X) 这个信息量的时候,H(X,Y)剩下的信息量就是条件熵:H(Y|X)=H(X,Y)−H(X)因此,可以这样理解,描述 X和 Y 所需的信息是描述 X 自己所需的信息,加上给定 X 的条件下具体化 Y所需的额外信息。关于条件熵的例子可以看这篇文章,讲得很详细。https://zhuanlan.zhihu.com/p/26551798
相对熵 (Relative entropy),也称KL散度 (Kullback–Leibler divergence)
设 p(x)、q(x) 是 离散随机变量 X 中取值的两个概率分布,则 p 对 q的相对熵是: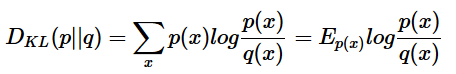
性质:
1、如果 p(x)和 q(x)两个分布相同,那么相对熵等于0
2、DKL(p||q)≠DKL(q||p),相对熵具有不对称性。大家可以举个简单例子算一下。
3、DKL(p||q)≥0证明如下(利用Jensen不等式https://en.wikipedia.org/wiki/Jensen%27s_inequality):
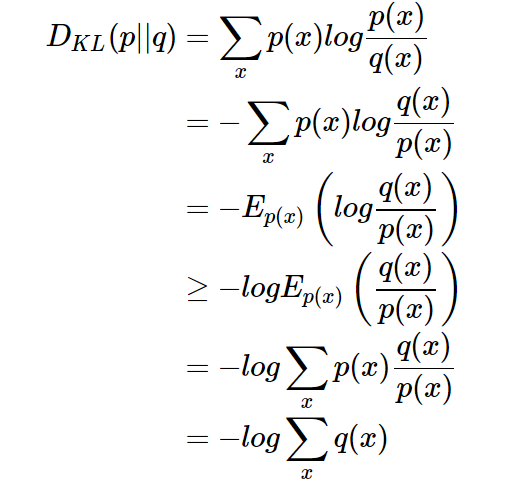
因为:
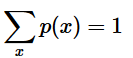
所以:
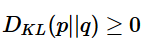
总结:相对熵可以用来衡量两个概率分布之间的差异,上面公式的意义就是求 p
与 q 之间的对数差在 p
上的期望值。
4、交叉熵 (Cross entropy)
现在有关于样本集的两个概率分布 p(x)
和 q(x),其中 p(x) 为真实分布, q(x) 非真实分布。如果用真实分布 p(x)
来衡量识别别一个样本所需要编码长度的期望(平均编码长度)为:
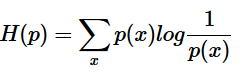
如果使用非真实分布 q(x)来表示来自真实分布 p(x)的平均编码长度,则是: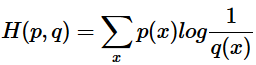 。(因为用 q(x) 来编码的样本来自于分布 q(x) ,所以 H(p,q) 中的概率是 p(x))。时就将 H(p,q) 称之为交叉熵。举个例子。考虑一个随机变量 x,真实分布
。(因为用 q(x) 来编码的样本来自于分布 q(x) ,所以 H(p,q) 中的概率是 p(x))。时就将 H(p,q) 称之为交叉熵。举个例子。考虑一个随机变量 x,真实分布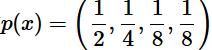 ,非真实分布
,非真实分布 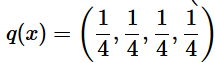 , 则H(p)=1.75 bits(最短平均码长),交叉熵
, 则H(p)=1.75 bits(最短平均码长),交叉熵 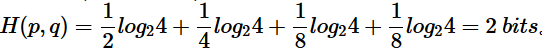 由此可以看出根据非真实分布 q(x) 得到的平均码长大于根据真实分布 p(x)得到的平均码长。我们再化简一下相对熵的公式。
由此可以看出根据非真实分布 q(x) 得到的平均码长大于根据真实分布 p(x)得到的平均码长。我们再化简一下相对熵的公式。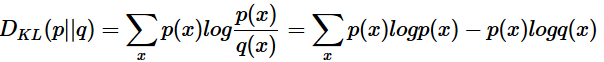
有没有发现什么?
熵的公式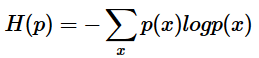
交叉熵的公式 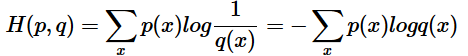
所以有: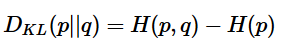 (当用非真实分布 q(x) 得到的平均码长比真实分布 p(x)
(当用非真实分布 q(x) 得到的平均码长比真实分布 p(x)
得到的平均码长多出的比特数就是相对熵)又因为 DKL(p||q)≥0,所以 H(p,q)≥H(p)(当 p(x)=q(x)时取等号,此时交叉熵等于信息熵)
并且当 H(p)为常量时(注:在机器学习中,训练数据分布是固定的),最小化相对熵 DKL(p||q) 等价于最小化交叉熵 H(p,q)
也等价于最大化似然估计(具体参考Deep Learning 5.5)。
在机器学习中,我们希望在训练数据上模型学到的分布 P(model)
和真实数据的分布 P(real) 越接近越好,所以我们可以使其相对熵最小。但是我们没有真实数据的分布,所以只能希望模型学到的分布 P(model) 和训练数据的分布 P(train)
尽量相同。假设训练数据是从总体中独立同分布采样的,那么我们可以通过最小化训练数据的经验误差来降低模型的泛化误差。即:
1.希望学到的模型的分布和真实分布一致,P(model)≃P(real)
2. 但是真实分布不可知,假设训练数据是从真实数据中独立同分布采样的,P(train)≃P(real)
3. 因此,我们希望学到的模型分布至少和训练数据的分布一致,P(train)≃P(model)
根据之前的描述,最小化训练数据上的分布 P(train)与最小化模型分布 P(model) 的差异等价于最小化相对熵,即 DKL(P(train)||P(model))。此时, P(train) 就是DKL(p||q) 中的 p,即真实分布,P(model) 就是 q。又因为训练数据的分布 p 是给定的,所以求 DKL(p||q) 等价于求 H(p,q)。得证,交叉熵可以用来计算学习模型分布与训练分布之间的差异。交叉熵广泛用于逻辑回归的Sigmoid和Softmax函数中作为损失函数使用。这篇文章先不说了。
5、总结
- 信息熵是衡量随机变量分布的混乱程度,是随机分布各事件发生的信息量的期望值,随机变量的取值个数越多,状态数也就越多,信息熵就越大,混乱程度就越大。当随机分布为均匀分布时,熵最大;信息熵推广到多维领域,则可得到联合信息熵;条件熵表示的是在 X给定条件下,Y 的条件概率分布的熵对 X的期望。
- 相对熵可以用来衡量两个概率分布之间的差异。
- 交叉熵可以来衡量在给定的真实分布下,使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小。
或者:
- 信息熵是传输一个随机变量状态值所需的比特位下界(最短平均编码长度)。
- 相对熵是指用 q
来表示分布 p
- 额外需要的编码长度。
- 交叉熵是指用分布 q
来表示本来表示分布 p 的平均编码长度
1.2 泰勒展开

2 知识铺垫
2.1 决策树
举个例子,集训营某一期有100多名学员,假定给你一个任务,要你统计男生女生各多少人,当一个一个学员依次上台站到你面前时,你会怎么区分谁是男谁是女呢?
很快,你考虑到男生的头发一般很短,女生的头发一般比较长,所以你通过头发的长短将这个班的所有学员分为两拨,长发的为“女”,短发为“男”。
相当于你依靠一个指标“头发长短”将整个班的人进行了划分,于是形成了一个简单的决策树,而划分的依据是头发长短。
这时,有的人可能有不同意见了:为什么要用“头发长短”划分呀,我可不可以用“穿的鞋子是否是高跟鞋”,“有没有喉结”等等这些来划分呢,答案当然是可以的。
但究竟根据哪个指标划分更好呢?很直接的判断是哪个分类效果更好则优先用哪个。所以,这时就需要一个评价标准来量化分类效果了。
怎么判断“头发长短”或者“是否有喉结”是最好的划分方式,效果怎么量化呢?直观上来说,如果根据某个标准分类人群后,纯度越高效果越好,比如说你分为两群,“女”那一群都是女的,“男”那一群全是男的,那这个效果是最好的。但有时实际的分类情况不是那么理想,所以只能说越接近这种情况,我们则认为效果越好。
量化分类效果的方式有很多,比如信息增益(ID3)、信息增益率(C4.5)、基尼系数(CART)等等。
信息增益的度量标准:熵
ID3算法的核心思想就是以信息增益度量属性选择,选择分裂后信息增益最大的属性进行分裂。
什么是信息增益呢?为了精确地定义信息增益,我们先定义信息论中广泛使用的一个度量标准,称为熵(entropy),它刻画了任意样例集的纯度(purity)。给定包含关于某个目标概念的正反样例的样例集S,那么S相对这个布尔型分类的熵为:
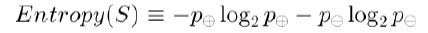
上述公式中,p+代表正样例,比如在本文开头第二个例子中p+则意味着去打羽毛球,而p-则代表反样例,不去打球(在有关熵的所有计算中我们定义0log0为0)。
举例来说,假设S是一个关于布尔概念的有14个样例的集合,它包括9个正例和5个反例(我们采用记号[9+,5-]来概括这样的数据样例),那么S相对于这个布尔样例的熵为:
Entropy([9+,5-])=-(9/14)log2(9/14)-(5/14)log2(5/14)=0.940。
So,根据上述这个公式,我们可以得到:
如果S的所有成员属于同一类,则Entropy(S)=0;
如果S的正反样例数量相等,则Entropy(S)=1;
如果S的正反样例数量不等,则熵介于0,1之间
如下图所示:
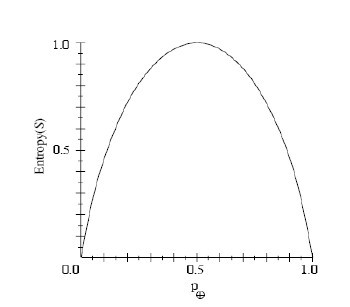
看到没,通过Entropy的值,你就能评估当前分类树的分类效果好坏了。
2.2 回归树与集成学习
如果用一句话定义xgboost,很简单:Xgboost就是由很多CART树集成。但,什么是CART树?
数据挖掘或机器学习中使用的决策树有两种主要类型:
分类树分析是指预测结果是数据所属的类(比如某个电影去看还是不看)
回归树分析是指预测结果可以被认为是实数(例如房屋的价格,或患者在医院中的逗留时间)
而术语分类回归树(CART,Classification And Regression Tree)分析是用于指代上述两种树的总称,由Breiman等人首先提出。
2.2.1 回归树
事实上,分类与回归是两个很接近的问题,分类的目标是根据已知样本的某些特征,判断一个新的样本属于哪种已知的样本类,它的结果是离散值。而回归的结果是连续的值。当然,本质是一样的,都是特征(feature)到结果/标签(label)之间的映射。
理清了什么是分类和回归之后,理解分类树和回归树就不难了。
分类树的样本输出(即响应值)是类的形式,比如判断这个救命药是真的还是假的,周末去看电影《风语咒》还是不去。而回归树的样本输出是数值的形式,比如给某人发放房屋贷款的数额就是具体的数值,可以是0到300万元之间的任意值。
所以,对于回归树,你没法再用分类树那套信息增益、信息增益率、基尼系数来判定树的节点分裂了,你需要采取新的方式评估效果,包括预测误差(常用的有均方误差、对数误差等)。而且节点不再是类别,是数值(预测值),那么怎么确定呢?有的是节点内样本均值,有的是最优化算出来的比如Xgboost。
CART回归树是假设树为二叉树,通过不断将特征进行分裂。比如当前树结点是基于第j个特征值进行分裂的,设该特征值小于s的样本划分为左子树,大于s的样本划分为右子树。
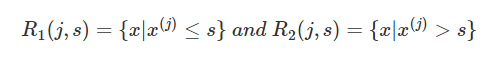
而CART回归树实质上就是在该特征维度对样本空间进行划分,而这种空间划分的优化是一种NP难问题,因此,在决策树模型中是使用启发式方法解决。典型CART回归树产生的目标函数为:
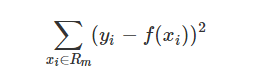
因此,当我们为了求解最优的切分特征j和最优的切分点s,就转化为求解这么一个目标函数:
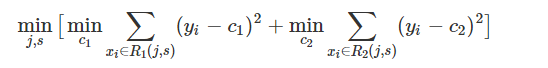
所以我们只要遍历所有特征的的所有切分点,就能找到最优的切分特征和切分点。最终得到一棵回归树。
2.2.2 集成学习
所谓集成学习,是指构建多个分类器(弱分类器)对数据集进行预测,然后用某种策略将多个分类器预测的结果集成起来,作为最终预测结果。通俗比喻就是“三个臭皮匠赛过诸葛亮”,或一个公司董事会上的各董事投票决策,它要求每个弱分类器具备一定的“准确性”,分类器之间具备“差异性”。
集成学习根据各个弱分类器之间有无依赖关系,分为Boosting和Bagging两大流派:
Boosting流派,各分类器之间有依赖关系,必须串行,比如Adaboost、GBDT(Gradient Boosting Decision Tree)、Xgboost
Bagging流派,各分类器之间没有依赖关系,可各自并行,比如随机森林(Random Forest)
而著名的Adaboost作为boosting流派中最具代表性的一种方法。
AdaBoost,是英文"Adaptive Boosting"(自适应增强)的缩写,由Yoav Freund和Robert Schapire在1995年提出。它的自适应在于:前一个基本分类器分错的样本会得到加强,加权后的全体样本再次被用来训练下一个基本分类器。同时,在每一轮中加入一个新的弱分类器,直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数。
具体说来,整个Adaboost 迭代算法就3步:
初始化训练数据的权值分布。如果有N个样本,则每一个训练样本最开始时都被赋予相同的权值:1/N。
训练弱分类器。具体训练过程中,如果某个样本点已经被准确地分类,那么在构造下一个训练集中,它的权值就被降低;相反,如果某个样本点没有被准确地分类,那么它的权值就得到提高。然后,权值更新过的样本集被用于训练下一个分类器,整个训练过程如此迭代地进行下去。
将各个训练得到的弱分类器组合成强分类器。各个弱分类器的训练过程结束后,加大分类误差率小的弱分类器的权重,使其在最终的分类函数中起着较大的决定作用,而降低分类误差率大的弱分类器的权重,使其在最终的分类函数中起着较小的决定作用。换言之,误差率低的弱分类器在最终分类器中占的权重较大,否则较小。
而另一种boosting方法GBDT(Gradient Boost Decision Tree),则与AdaBoost不同,GBDT每一次的计算是都为了减少上一次的残差,进而在残差减少(负梯度)的方向上建立一个新的模型。
boosting集成学习由多个相关联的决策树联合决策,什么叫相关联?举个例子
有一个样本[数据->标签]是:[(2,4,5)-> 4]
第一棵决策树用这个样本训练的预测为3.3
那么第二棵决策树训练时的输入,这个样本就变成了:[(2,4,5)-> 0.7]
也就是说,下一棵决策树输入样本会与前面决策树的训练和预测相关
很快你会意识到,Xgboost为何也是一个boosting的集成学习了。
而一个回归树形成的关键点在于:
分裂点依据什么来划分(如前面说的均方误差最小,loss);
分类后的节点预测值是多少(如前面说,有一种是将叶子节点下各样本实际值得均值作为叶子节点预测误差,或者计算所得)
至于另一类集成学习方法,比如Random Forest(随机森林)算法,各个决策树是独立的、每个决策树在样本堆里随机选一批样本,随机选一批特征进行独立训练,各个决策树之间没有啥关系。本文暂不展开介绍。
3.xgGBDT原理
说到Xgboost,不得不先从GBDT(Gradient Boosting Decision Tree)说起。因为xgboost本质上还是一个GBDT,但是力争把速度和效率发挥到极致,所以叫X (Extreme) GBoosted。包括前面说过,两者都是boosting方法。
GBDT的原理很简单,就是所有弱分类器的结果相加等于预测值,然后下一个弱分类器去拟合误差函数对预测值的梯度/残差(这个梯度/残差就是预测值与真实值之间的误差)。当然了,它里面的弱分类器的表现形式就是各棵树。如图所示:Y = Y1 + Y2 + Y3。
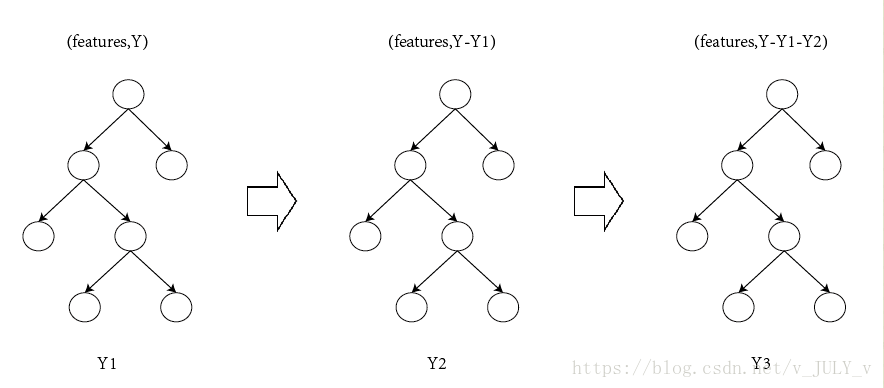
举一个非常简单的例子,比如我今年30岁了,但计算机或者模型GBDT并不知道我今年多少岁,那GBDT咋办呢?
它会在第一个弱分类器(或第一棵树中)随便用一个年龄比如20岁来拟合,然后发现误差有10岁;
接下来在第二棵树中,用6岁去拟合剩下的损失,发现差距还有4岁;
接着在第三棵树中用3岁拟合剩下的差距,发现差距只有1岁了;
最后在第四课树中用1岁拟合剩下的残差,完美。
最终,四棵树的结论加起来,就是真实年龄30岁。实际工程中,gbdt是计算负梯度,用负梯度近似残差。
注意,为何gbdt可以用用负梯度近似残差呢?
回归任务下,GBDT 在每一轮的迭代时对每个样本都会有一个预测值,此时的损失函数为均方差损失函数,
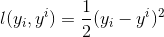
那此时的负梯度是这样计算的
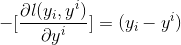
所以,当损失函数选用均方损失函数是时,每一次拟合的值就是(真实值 - 当前模型预测的值),即残差。此时的变量是,即“当前预测模型的值”,也就是对它求负梯度。
另外,这里还得再啰嗦一下,上面预测年龄的第一个步骤中的“随便”二字看似随便,其实深入思考一下一点都不随便,你会发现大部分做预测的模型,基本都是这么个常规套路,先随便用一个值去预测,然后对比预测值与真实值的差距,最后不断调整 缩小差距。所以会出来一系列目标函数:确定目标,和损失函数:缩小误差。
再进一步思考,你会发现这完全符合人类做预测的普遍常识、普遍做法,当对一个事物不太了解时,一开始也是根据经验尝试、初探,直到逼近某种意义上的接近或者完全吻合。
还是年龄预测的例子。
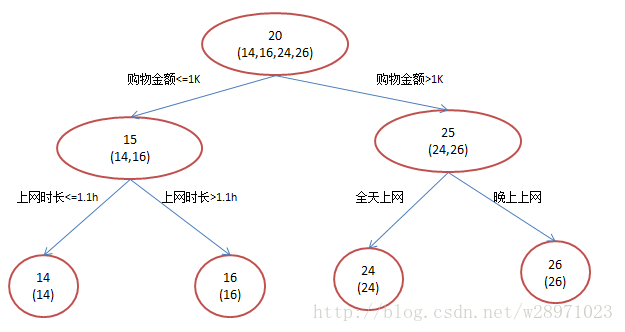
简单起见,假定训练集只有4个人:A,B,C,D,他们的年龄分别是14,16,24,26。其中A、B分别是高一和高三学生;C,D分别是应届毕业生和工作两年的员工。
所以,现在的问题就是我们要预测这4个人的年龄,咋下手?很简单,先随便用一个年龄比如20岁去拟合他们,然后根据实际情况不断调整。
如果是用一棵传统的回归决策树来训练,会得到如下图所示结果:
现在我们使用GBDT来做这件事,由于数据太少,我们限定叶子节点做多有两个,即每棵树都只有一个分枝,并且限定只学两棵树。
我们会得到如下图所示结果:
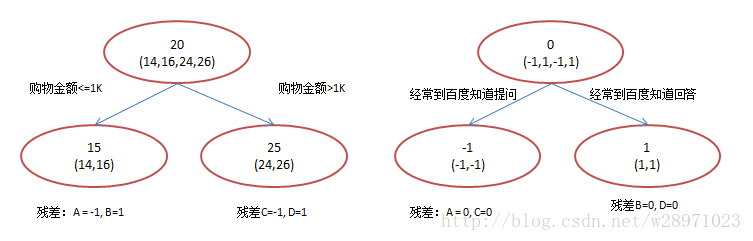
在第一棵树分枝和图1一样,由于A,B年龄较为相近,C,D年龄较为相近,他们被分为左右两拨,每拨用平均年龄作为预测值。
此时计算残差(残差的意思就是:A的实际值 - A的预测值 = A的残差),所以A的残差就是实际值14 - 预测值15 = 残差值-1。
注意,A的预测值是指前面所有树累加的和,这里前面只有一棵树所以直接是15,如果还有树则需要都累加起来作为A的预测值。
残差在数理统计中是指实际观察值与估计值(拟合值)之间的差。“残差”蕴含了有关模型基本假设的重要信息。如果回归模型正确的话, 我们可以将残差看作误差的观测值。
进而得到A,B,C,D的残差分别为-1,1,-1,1。
然后拿它们的残差-1、1、-1、1代替A B C D的原值,到第二棵树去学习,第二棵树只有两个值1和-1,直接分成两个节点,即A和C分在左边,B和D分在右边,经过计算(比如A,实际值-1 - 预测值-1 = 残差0,比如C,实际值-1 - 预测值-1 = 0),此时所有人的残差都是0。
残差值都为0,相当于第二棵树的预测值和它们的实际值相等,则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了,即每个人都得到了真实的预测值。
换句话说,现在A,B,C,D的预测值都和真实年龄一致了。Perfect!
A: 14岁高一学生,购物较少,经常问学长问题,预测年龄A = 15 – 1 = 14
B: 16岁高三学生,购物较少,经常被学弟问问题,预测年龄B = 15 + 1 = 16
C: 24岁应届毕业生,购物较多,经常问师兄问题,预测年龄C = 25 – 1 = 24
D: 26岁工作两年员工,购物较多,经常被师弟问问题,预测年龄D = 25 + 1 = 26
所以,GBDT需要将多棵树的得分累加得到最终的预测得分,且每一次迭代,都在现有树的基础上,增加一棵树去拟合前面树的预测结果与真实值之间的残差。
3.1 xgboost树的定义
本节的示意图基本引用自xgboost原作者陈天奇的讲义PPT中。
举个例子,我们要预测一家人对电子游戏的喜好程度,考虑到年轻和年老相比,年轻更可能喜欢电子游戏,以及男性和女性相比,男性更喜欢电子游戏,故先根据年龄大小区分小孩和大人,然后再通过性别区分开是男是女,逐一给各人在电子游戏喜好程度上打分,如下图所示。
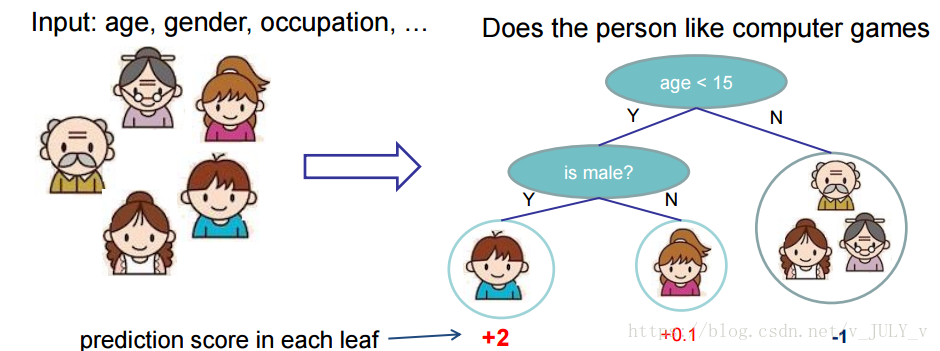
就这样,训练出了2棵树tree1和tree2,类似之前gbdt的原理,两棵树的结论累加起来便是最终的结论,所以小孩的预测分数就是两棵树中小孩所落到的结点的分数相加:2 + 0.9 = 2.9。爷爷的预测分数同理:-1 + (-0.9)= -1.9。具体如下图所示
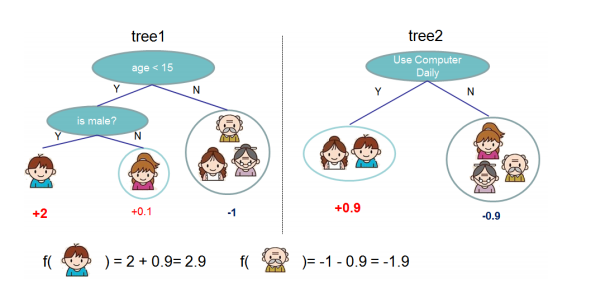
恩,你可能要拍案而起了,惊呼,这不是跟上文介绍的gbdt乃异曲同工么?
事实上,如果不考虑工程实现、解决问题上的一些差异,xgboost与gbdt比较大的不同就是目标函数的定义。xgboost的目标函数如下图所示:
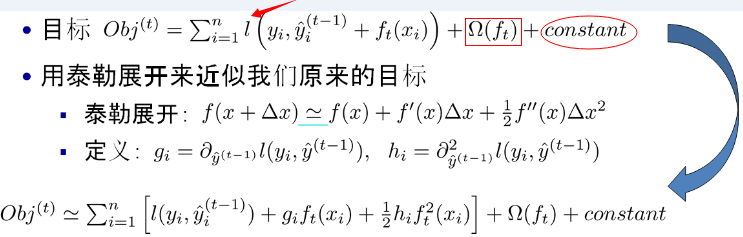
其中
红色箭头所指向的L 即为损失函数(比如平方损失函数: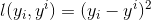 ,或logistic损失函数:
,或logistic损失函数: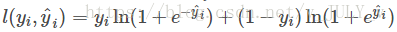 )
)
红色方框所框起来的是正则项(包括L1正则、L2正则)
红色圆圈所圈起来的为常数项
对于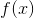 ,xgboost利用泰勒展开三项,做一个近似
,xgboost利用泰勒展开三项,做一个近似
我们可以很清晰地看到,最终的目标函数只依赖于每个数据点在误差函数上的一阶导数和二阶导数。
额,峰回路转,突然丢这么大一个公式,不少人可能瞬间就懵了。没事,下面咱们来拆解下这个目标函数,并一一剖析每个公式、每个符号、每个下标的含义。
3.2 xgboost目标函数
xgboost的核心算法思想不难,基本就是
不断地添加树,不断地进行特征分裂来生长一棵树,每次添加一个树,其实是学习一个新函数,去拟合上次预测的残差。
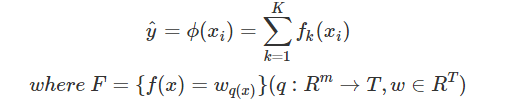
注:w_q(x)为叶子节点q的分数,对应了所有K棵回归树(regression tree)的集合,而f(x)为其中一棵回归树。
当我们训练完成得到k棵树,我们要预测一个样本的分数,其实就是根据这个样本的特征,在每棵树中会落到对应的一个叶子节点,每个叶子节点就对应一个分数
最后只需要将每棵树对应的分数加起来就是该样本的预测值。
显然,我们的目标是要使得树群的预测值尽量接近真实值,而且有尽量大的泛化能力。
所以,从数学角度看这是一个泛函最优化问题,故把目标函数简化如下:
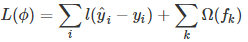
如你所见,这个目标函数分为两部分:损失函数和正则化项。且损失函数揭示训练误差(即预测分数和真实分数的差距),正则化定义复杂度。
对于上式而言,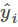 是整个累加模型的输出,正则化项
是整个累加模型的输出,正则化项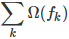 是则表示树的复杂度的函数,值越小复杂度越低,泛化能力越强,其表达式为
是则表示树的复杂度的函数,值越小复杂度越低,泛化能力越强,其表达式为
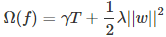
T表示叶子节点的个数,w表示叶子节点的分数。直观上看,目标要求预测误差尽量小,且叶子节点T尽量少(γ控制叶子结点的个数),节点数值w尽量不极端(λ控制叶子节点的分数不会过大),防止过拟合。
插一句,一般的目标函数都包含下面两项

其中,误差/损失函数鼓励我们的模型尽量去拟合训练数据,使得最后的模型会有比较少的 bias。而正则化项则鼓励更加简单的模型。因为当模型简单之后,有限数据拟合出来结果的随机性比较小,不容易过拟合,使得最后模型的预测更加稳定。
3.2 模型学习与训练误差
具体来说,目标函数第一部分中的 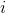
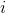
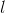
−
) 表示第
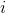
类似之前GBDT的套路,xgboost也是需要将多棵树的得分累加得到最终的预测得分(每一次迭代,都在现有树的基础上,增加一棵树去拟合前面树的预测结果与真实值之间的残差)。

但,我们如何选择每一轮加入什么呢?答案是非常直接的,选取一个 来使得我们的目标函数尽量最大地降低。
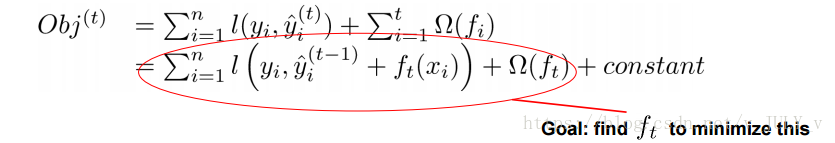
再强调一下,考虑到第t轮的模型预测值 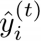 = 前t-1轮的模型预测
= 前t-1轮的模型预测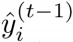 +
+ 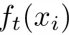 ,因此误差函数记为:
,因此误差函数记为: 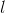
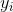
![]() +
+ ![]() ),后面一项为正则化项。
),后面一项为正则化项。
对于这个误差函数的式子而言,在第t步,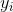
![]() 可由上一步第t-1步中的
可由上一步第t-1步中的![]() 加上
加上![]() 计算所得,某种意义上也算已知值,故模型学习的是
计算所得,某种意义上也算已知值,故模型学习的是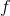
上面那个Obj的公式表达的可能有些过于抽象,我们可以考虑当 是平方误差的情况(相当于),这个时候我们的目标可以被写成下面这样的二次函数(图中画圈的部分表示的就是预测值和真实值之间的残差):
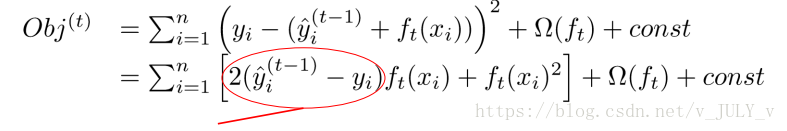
更加一般的,损失函数不是二次函数咋办?利用泰勒展开,不是二次的想办法近似为二次(如你所见,定义了一阶导和二阶导)。

恩恩,注意了!不少人可能就会在这里卡壳,网上也很少有文章解释清楚,在和七月在线AI lab陈博士讨论之后,发现这里面最关键的其实就是把泰勒二阶展开各项和xgboost 目标函数的对应关系搞清楚,相当于我们可以利用泰勒二阶展开去做目标函数的近似。
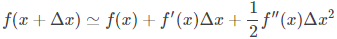
对应到xgboost的目标函数里头
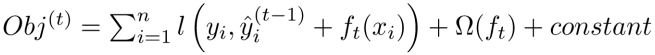
忽略损失函数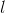
![]() (别忘了上面说的“ 在第t步,
(别忘了上面说的“ 在第t步,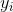
 的偏导计算),做下一一对应:
的偏导计算),做下一一对应:
- 泰勒二阶展开f 里的x对应目标函数里的
![]() ,
, - f 里
![]() 的对应目标函数的
的对应目标函数的![]() ,
, - 从而f 对x求导数时,对应为目标函数对
![]() 求偏导
求偏导
得到:
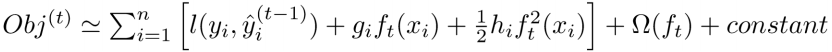
其中,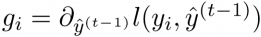 ,
,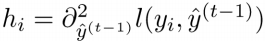
呜呼,透了!不过,这个转化过程中的关键泰勒二次展开到底是哪来的呢?
在数学中,泰勒公式(英语:Taylor's Formula)是一个用函数在某点的信息描述其附近取值的公式。这个公式来自于微积分的泰勒定理(Taylor's theorem),泰勒定理描述了一个可微函数,如果函数足够光滑的话,在已知函数在某一点的各阶导数值的情况之下,泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值,这个多项式称为泰勒多项式(Taylor polynomial)。
相当于告诉我们可由利用泰勒多项式的某些次项做原函数的近似。
泰勒定理:
设 n 是一个正整数。如果定义在一个包含 a 的区间上的函数 f 在 a 点处 n+1 次可导,那么对于这个区间上的任意 x,都有:
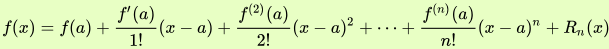
其中的多项式称为函数在a 处的泰勒展开式,剩余的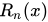 是泰勒公式的余项,是
是泰勒公式的余项,是![]() 的高阶无穷小。
的高阶无穷小。
接下来,考虑到我们的第t 颗回归树是根据前面的t-1颗回归树的残差得来的,相当于t-1颗树的值![]() 是已知的。换句话说,
是已知的。换句话说,![]() 对目标函数的优化不影响,可以直接去掉,且常数项也可以移除,从而得到如下一个比较统一的目标函数。
对目标函数的优化不影响,可以直接去掉,且常数项也可以移除,从而得到如下一个比较统一的目标函数。
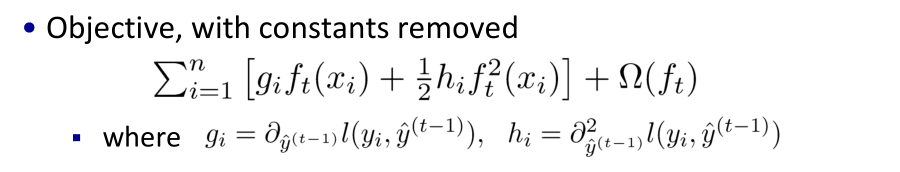
这时,目标函数只依赖于每个数据点在误差函数上的一阶导数和二阶导数(相信你已经看出xgboost和gbdt的不同了,目标函数保留了泰勒展开的二次项)。
总的指导原则如就职Google的读者crab6789所说:
实质是把样本分配到叶子结点会对应一个obj,优化过程就是obj优化。也就是分裂节点到叶子不同的组合,不同的组合对应不同obj,所有的优化围绕这个思想展开。
到目前为止我们讨论了目标函数中的第一个部分:训练误差。接下来我们讨论目标函数的第二个部分:正则项,即如何定义树的复杂度。
3.3 正则项:树的复杂度
首先,梳理下几个规则
用叶子节点集合以及叶子节点得分表示
每个样本都落在一个叶子节点上
q(x)表示样本x在某个叶子节点上,wq(x)是该节点的打分,即该样本的模型预测值
所以当我们把树成结构部分q和叶子权重部分w后,结构函数q把输入映射到叶子的索引号上面去,而w给定了每个索引号对应的叶子分数是什么。
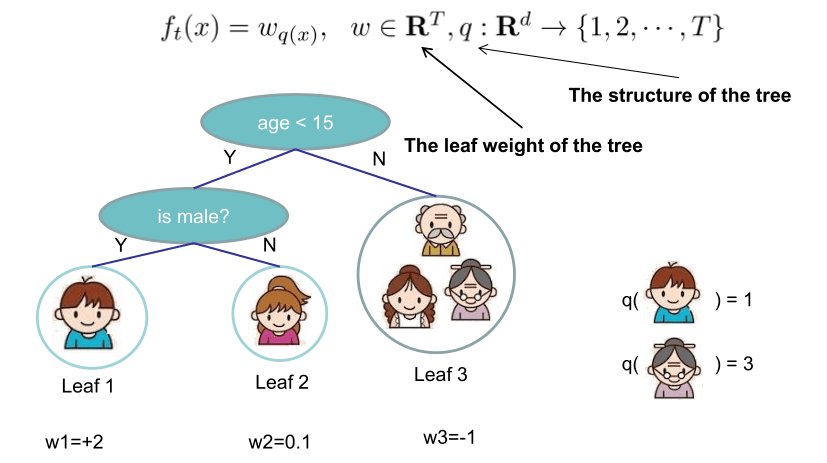
另外,如下图所示,xgboost对树的复杂度包含了两个部分:
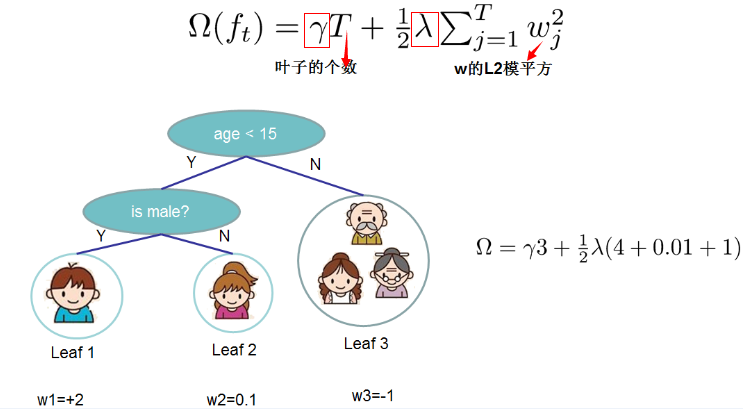
一个是树里面叶子节点的个数T
一个是树上叶子节点的得分w的L2模平方(对w进行L2正则化,相当于针对每个叶结点的得分增加L2平滑,目的是为了避免过拟合)
在这种新的定义下,我们可以把之前的目标函数进行如下变形(另,别忘了: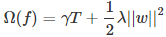
)
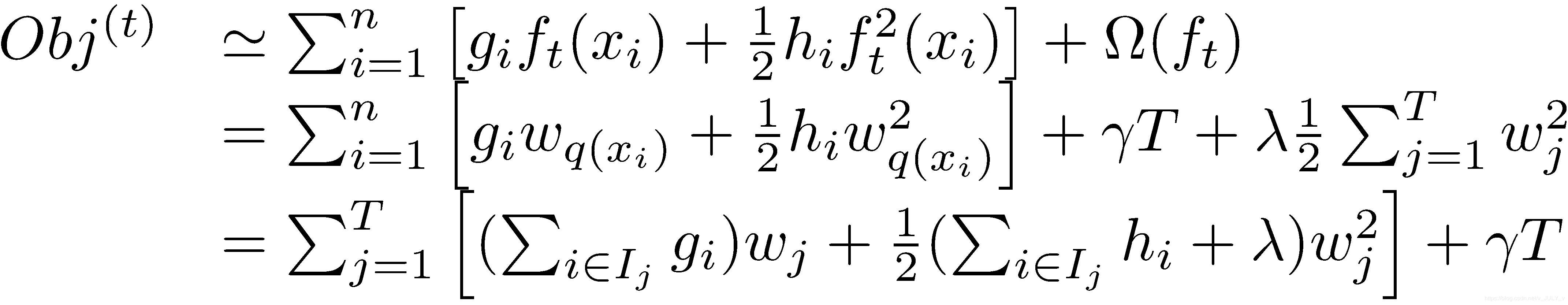
其中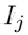
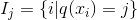
从而,加了正则项的目标函数里就出现了两种累加
一种是 - > n(样本数)
一种是 -> T(叶子节点数)
这一个目标包含了T个相互独立的单变量二次函数。
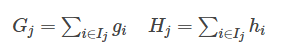
最终公式可以化简为

通过对
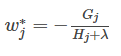
然后把
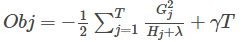
3.3 打分函数计算
Obj代表了当我们指定一个树的结构的时候,我们在目标上面最多减少多少。我们可以把它叫做结构分数(structure score)
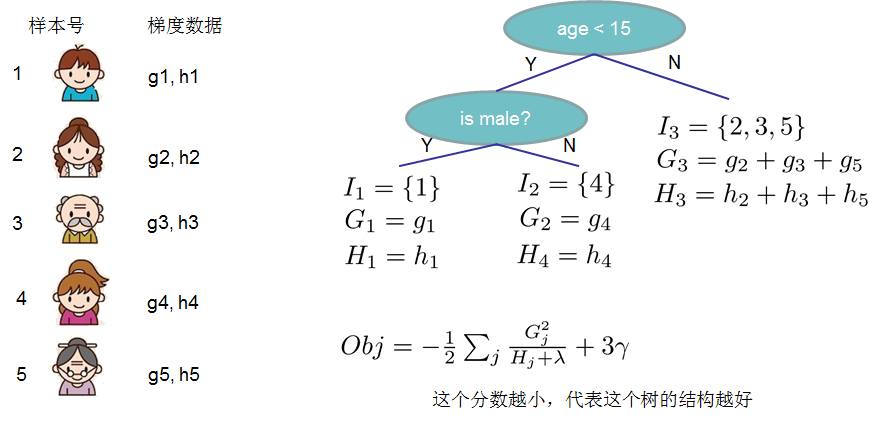
3.3.1 分裂节点
很有意思的一个事是,我们从头到尾了解了xgboost如何优化、如何计算,但树到底长啥样,我们却一直没看到。很显然,一棵树的生成是由一个节点一分为二,然后不断分裂最终形成为整棵树。那么树怎么分裂的就成为了接下来我们要探讨的关键。
对于一个叶子节点如何进行分裂,xgboost作者在其原始论文中给出了两种分裂节点的方法
(1)枚举所有不同树结构的贪心法
现在的情况是只要知道树的结构,就能得到一个该结构下的最好分数,那如何确定树的结构呢?
一个想当然的方法是:不断地枚举不同树的结构,然后利用打分函数来寻找出一个最优结构的树,接着加入到模型中,不断重复这样的操作。而再一想,你会意识到要枚举的状态太多了,基本属于无穷种,那咋办呢?
我们试下贪心法,从树深度0开始,每一节点都遍历所有的特征,比如年龄、性别等等,然后对于某个特征,先按照该特征里的值进行排序,然后线性扫描该特征进而确定最好的分割点,最后对所有特征进行分割后,我们选择所谓的增益Gain最高的那个特征,而Gain如何计算呢?
还记得4.2节最后,我们得到的计算式子吧?
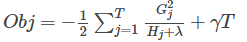
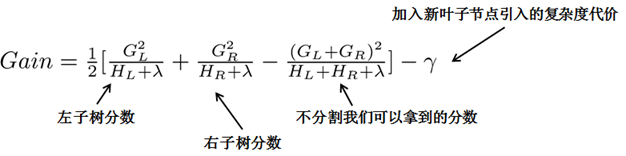
换句话说,目标函数中的G/(H+λ)部分,表示着每一个叶子节点对当前模型损失的贡献程度,融合一下,得到Gain的计算表达式,如下所示:
第一个值得注意的事情是“对于某个特征,先按照该特征里的值进行排序”,这里举个例子。
比如设置一个值a,然后枚举所有x < a、a < x这样的条件(x代表某个特征比如年龄age,把age从小到大排序:假定从左至右依次增大,则比a小的放在左边,比a大的放在右边),对于某个特定的分割a,我们要计算a左边和右边的导数和。
比如总共五个人,按年龄排好序后,一开始我们总共有如下4种划分方法:
把第一个人和后面四个人划分开
把前两个人和后面三个人划分开
把前三个人和后面两个人划分开
把前面四个人和后面一个人划分开
接下来,把上面4种划分方法全都各自计算一下Gain,看哪种划分方法得到的Gain值最大则选取哪种划分方法,经过计算,发现把第2种划分方法“前面两个人和后面三个人划分开”得到的Gain值最大,意味着在一分为二这个第一层层面上这种划分方法是最合适的。
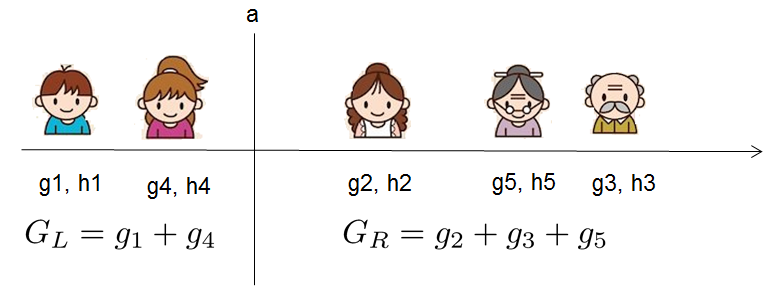
换句话说,对于所有的特征x,我们只要做一遍从左到右的扫描就可以枚举出所有分割的梯度和GL和GR。然后用计算Gain的公式计算每个分割方案的分数就可以了。
然后后续则依然按照这种划分方法继续第二层、第三层、第四层、第N层的分裂。
第二个值得注意的事情就是引入分割不一定会使得情况变好,所以我们有一个引入新叶子的惩罚项。优化这个目标对应了树的剪枝, 当引入的分割带来的增益小于一个阀值γ 的时候,则忽略这个分割。
换句话说,当引入某项分割,结果分割之后得到的分数 - 不分割得到的分数得到的值太小(比如小于我们的最低期望阀值γ),但却因此得到的复杂度过高,则相当于得不偿失,不如不分割。即做某个动作带来的好处比因此带来的坏处大不了太多,则为避免复杂 多一事不如少一事的态度,不如不做。
相当于在我们发现“分”还不如“不分”的情况下后(得到的增益太小,小到小于阈值γ),会有2个叶子节点存在同一棵子树上的情况。
下面是论文中的算法

(2)近似算法
主要针对数据太大,不能直接进行计算

就职于Google的读者crab6789点评:
把样本从根分配到叶子结点,就是个排列组合。不同的组合对应的cost不同。求最好的组合你就要try,一味穷举是不可能的,所以才出来贪婪法。不看从头到尾 就看当下节点怎么分配最好。这才有了那个exact greddy方法,后来还想加速才有了histogram的做法。
3.4 小结:Boosted Tree Algorithm
总结一下,如图所示

咱们来再次回顾整个过程。
如果某个样本label数值为4,那么第一个回归树预测3,第二个预测为1; 另外一组回归树,一个预测2,一个预测2,那么倾向后一种,为什么呢?前一种情况,第一棵树学的太多,太接近4,也就意味着有较大的过拟合的风险。
OK,听起来很美好,可是怎么实现呢,上面这个目标函数跟实际的参数怎么联系起来,记得我们说过,回归树的参数:
选取哪个feature分裂节点呢
节点的预测值(总不能靠取平均值这么粗暴不讲道理的方式吧,好歹高级一点)
最终的策略就是:贪心 + 最优化(对的,二次最优化) 。
通俗解释贪心策略:就是决策时刻按照当前目标最优化决定,说白了就是眼前利益最大化决定,“目光短浅”策略。
这里是怎么用贪心策略的呢,刚开始你有一群样本,放在第一个节点,这时候T=1,w多少呢,不知道,是求出来的,这时候所有样本的预测值都是w,带入样本的label数值,此时loss function变为
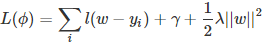
如果这里的l(w−yi)误差表示用的是平方误差,那么上述函数就是一个关于w的二次函数求最小值,取最小值的点就是这个节点的预测值,最小的函数值为最小损失函数。
本质上来讲,这就是一个二次函数最优化问题!但要是损失函数不是二次函数咋办?泰勒展开,不是二次的想办法近似为二次。
接着来,接下来要选个feature分裂成两个节点,变成一棵弱小的树苗,那么需要:
确定分裂用的feature,how?最简单的是粗暴的枚举/穷举(嗯,够粗暴),然后选择loss function效果最好的那个;
如何确立节点的w以及最小的loss function,大声告诉我怎么做?对,二次函数的求最值(计算二次的最值一般都有固定套路,即导数等于0的点) 。所以,选择一个feature分裂,计算loss function最小值,然后再选一个feature分裂,又得到一个loss function最小值,你枚举完,找一个效果最好的,把树给分裂,就得到了小树苗。
在分裂的时候,你可以注意到,每次节点分裂,loss function被影响的只有这个节点的样本,因而每次分裂,计算分裂的增益(loss function的降低量)只需要关注打算分裂的那个节点的样本。
总而言之,XGBoost使用了和CART回归树一样的想法,利用贪婪算法,遍历所有特征的所有特征划分点,不同的是使用的目标函数不一样。具体做法就是分裂后的目标函数值比单子叶子节点的目标函数的增益,同时为了限制树生长过深,还加了个阈值,只有当增益大于该阈值才进行分裂。
以下便为设定的阈值
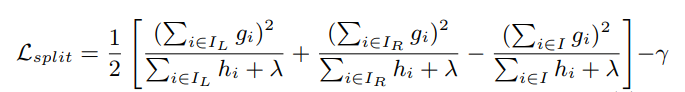
从而继续分裂,形成一棵树,再形成一棵树,每次在上一次的预测基础上取最优进一步分裂/建树,是不是贪心策略?
凡是这种循环迭代的方式必定有停止条件,什么时候停止呢?简言之,设置树的最大深度、当样本权重和小于设定阈值时停止生长以防止过拟合。具体而言,则
当引入的分裂带来的增益小于设定阀值的时候,我们可以忽略掉这个分裂,所以并不是每一次分裂loss function整体都会增加的,有点预剪枝的意思,阈值参数为(即正则项里叶子节点数T的系数);
当树达到最大深度时则停止建立决策树,设置一个超参数max_depth,避免树太深导致学习局部样本,从而过拟合;
当样本权重和小于设定阈值时则停止建树。什么意思呢,即涉及到一个超参数-最小的样本权重和min_child_weight,和GBM的 min_child_leaf 参数类似,但不完全一样。大意就是一个叶子节点样本太少了,也终止同样是防止过拟合;
貌似看到过有树的最大数量的…
4、xgboost 代码实现及参数优化
4.1 参数调整注意事项
参数调整是机器学习中的一门黑暗艺术,模型的最佳参数可能取决于许多场景。所以不可能为此创建一个全面的指南。
了解偏差 - 方差权衡
如果您参加机器学习或统计学课程,这可能是最重要的概念之一。当我们允许模型变得更复杂(例如更深)时,模型具有更好的拟合训练数据的能力,从而导致模型偏差较小。但是,这种复杂的模型需要更多的数据才能适应。
XGBoost中的大多数参数都是关于偏差方差权衡。最好的模型应该仔细地将模型复杂性与其预测能力进行交换。 参数文档将告诉您每个参数是否会使模型更加保守。这可以用来帮助你在复杂的模型和简单的模型之间转动旋钮。
控制过度拟合
当您观察到高训练精度但测试精度低时,您可能会遇到过度拟合问题。
通常有两种方法可以控制XGBoost中的过度拟合:
- 第一种方法是直接控制模型复杂性。
- 这包括
max_depth,min_child_weight和gamma。
- 这包括
- 第二种方法是增加随机性,使训练对噪声具有鲁棒性。
- 这包括
subsample和colsample_bytree。 - 您还可以减少步长
eta。num_round当你这样做时记得增加。
- 这包括
处理不平衡数据集
对于广告点击日志等常见情况,数据集极不平衡。这可能会影响XGBoost模型的培训,有两种方法可以改进它。
- 如果您只关心预测的整体性能指标(AUC)
- 通过平衡正负权重
scale_pos_weight - 使用AUC进行评估
- 通过平衡正负权重
- 如果你关心预测正确的概率
- 在这种情况下,您无法重新平衡数据集
- 将参数设置
max_delta_step为有限数(例如1)以帮助收敛
4.2 参数说明
在运行XGBoost之前,我们必须设置三种类型的参数:通用参数,增压器参数和任务参数。
- 一般参数涉及我们用于增强的助推器,通常是树或线性模型
- 助推器参数取决于您选择的助推器
- 学习任务参数决定学习场景。例如,回归任务可以使用与排名任务不同的参数。
- 命令行参数与CLI版本的XGBoost的行为有关。
一般参数
booster[default =gbtree]- 使用哪种助推器。可以
gbtree,gblinear或dart;gbtree并dart使用基于树的模型,同时gblinear使用线性函数。
- 使用哪种助推器。可以
silent[default = 0] [已弃用]- 已过时。请
verbosity改用。
- 已过时。请
verbosity[默认= 1]- 打印消息的详细程度。有效值为0(静默),1(警告),2(信息),3(调试)。有时,XGBoost会尝试根据启发式更改配置,启动式显示为警告消息。如果出现意外行为,请尝试增加详细程度。
nthread[默认为未设置的最大线程数]- 用于运行XGBoost的并行线程数
disable_default_eval_metric[默认= 0]- 标记以禁用默认度量标准。设置为> 0以禁用。
num_pbuffer[由XGBoost自动设置,无需用户设置]- 预测缓冲区的大小,通常设置为训练实例的数量。缓冲区用于保存最后一次增强步骤的预测结果。
num_feature[由XGBoost自动设置,无需用户设置]- 用于增强的特征尺寸,设置为特征的最大尺寸
Tree Booster的参数
-
eta[default = 0.3,别名:learning_rate]- 更新中使用的步长缩小以防止过度拟合。在每个提升步骤之后,我们可以直接获得新特征的权重,并
eta缩小特征权重以使提升过程更加保守。 - 范围:[0,1]
- 更新中使用的步长缩小以防止过度拟合。在每个提升步骤之后,我们可以直接获得新特征的权重,并
-
gamma[default = 0,别名:min_split_loss]- 在树的叶节点上进行进一步分区所需的最小损耗减少。越大
gamma,算法越保守。 - 范围:[0,∞]
- 在树的叶节点上进行进一步分区所需的最小损耗减少。越大
-
max_depth[默认= 6]- 树的最大深度。增加此值将使模型更复杂,更容易过度拟合。
lossguided当tree_method设置为as时,仅在增长策略中接受0 ,hist并且它表示没有深度限制。请注意,在训练深树时,XGBoost会积极地消耗内存。 - range:[0,∞](
lossguided当tree_method设置为as时,仅在增长策略中接受0hist)
- 树的最大深度。增加此值将使模型更复杂,更容易过度拟合。
-
min_child_weight[默认= 1]- 儿童所需的实例重量(粗麻布)的最小总和。如果树分区步骤导致叶节点的实例权重之和小于
min_child_weight,则构建过程将放弃进一步的分区。在线性回归任务中,这仅对应于每个节点中需要的最小实例数。越大min_child_weight,算法越保守。 - 范围:[0,∞]
- 儿童所需的实例重量(粗麻布)的最小总和。如果树分区步骤导致叶节点的实例权重之和小于
-
max_delta_step[默认= 0]- 我们允许每个叶子输出的最大增量步长。如果该值设置为0,则表示没有约束。如果将其设置为正值,则可以帮助使更新步骤更加保守。通常不需要此参数,但当类非常不平衡时,它可能有助于逻辑回归。将其设置为值1-10可能有助于控制更新。
- 范围:[0,∞]
-
subsample[默认= 1]- 训练实例的子样本比率。将其设置为0.5意味着XGBoost会在生长树之前随机抽取一半训练数据。这样可以防止过度拟合。子采样将在每次增强迭代中发生一次。
- 范围:(0,1)
-
colsample_bytree,colsample_bylevel,colsample_bynode[默认= 1] -这是对列的子采样参数家族。- 所有colsample_by*参数的范围均为(0,1),默认值为1,和指定要进行二次采样的列的分数。
colsample_bytree是构造每棵树时列的子采样率。对于构造的每个树,子采样发生一次。colsample_bylevel是每个级别的列的子采样率。对于树中达到的每个新深度级别,子采样都会发生一次。列是从为当前树选择的列集中进行子采样的。colsample_bynode是每个节点(拆分)的列的子采样率。每次评估新的拆分时,都会发生一次子采样。列是从为当前级别选择的列集中进行二次采样的。colsample_by*参数累积起作用。例如,与64个功能的组合将在每次拆分时留下8个功能可供选择。{'colsample_bytree':0.5, 'colsample_bylevel':0.5, 'colsample_bynode':0.5}
-
lambda[default = 1,别名:reg_lambda]- 关于权重的L2正则化项。增加此值将使模型更加保守。
-
alpha[default = 0,别名:reg_alpha]- 关于权重的L1正则化项。增加此值将使模型更加保守。
-
tree_methodstring [default =auto]- XGBoost中使用的树构造算法。参见参考文献中的描述。
- XGBoost支持
hist和approx分布式培训,仅支持approx外部存储器版本。 - 选择:
auto,exact,approx,hist,gpu_exact,gpu_histauto:使用启发式方法选择最快的方法。- 对于中小型数据集,
exact将使用精确的贪婪()。 - 对于非常大的数据集,
approx将选择近似算法()。 - 因为旧行为总是在单个机器中使用精确贪婪,所以当选择近似算法来通知该选择时,用户将得到消息。
- 对于中小型数据集,
exact:精确的贪婪算法。approx:使用分位数草图和梯度直方图的近似贪婪算法。hist:快速直方图优化近似贪心算法。它使用了一些性能改进,例如垃圾箱缓存。gpu_exact:GPU实现exact算法。gpu_hist:GPU实现hist算法。
-
sketch_eps[默认= 0.03]- 仅用于
tree_method=approx。 - 这大致可以转化为箱数。与直接选择的箱数相比,这提供了具有草图精度的理论保证。
O(1 / sketch_eps) - 通常用户不必调整它。但考虑设置较低的数字,以便更准确地计算分割候选者。
- 范围:(0,1)
- 仅用于
-
scale_pos_weight[默认= 1] -
updater[default =grow_colmaker,prune]- 逗号分隔的字符串,用于定义要运行的树更新程序序列,提供构建和修改树的模块化方法。这是一个高级参数,通常会自动设置,具体取决于其他一些参数。但是,它也可以由用户明确设置。存在以下更新程序插件:
grow_colmaker:非分布式基于列的树构造。distcol:分布式树构造,具有基于列的数据分割模式。grow_histmaker:基于行式数据分割的分布式树构造,基于全局直方图计数提议。grow_local_histmaker:基于局部直方图计数。grow_skmaker:使用近似草绘算法。sync:同步所有分布式节点中的树。refresh:根据当前数据刷新树的统计信息和/或叶值。请注意,不会执行数据行的随机子采样。prune:修剪损失<min_split_loss(或gamma)的分裂。
- 在分布式设置中,隐式更新程序序列值将
grow_histmaker,prune默认调整为,您可以设置tree_method为hist使用grow_histmaker。
- 逗号分隔的字符串,用于定义要运行的树更新程序序列,提供构建和修改树的模块化方法。这是一个高级参数,通常会自动设置,具体取决于其他一些参数。但是,它也可以由用户明确设置。存在以下更新程序插件:
-
refresh_leaf[默认= 1]- 这是
refreshupdater插件的参数。当此标志为1时,将更新树叶和树节点的统计信息。当它为0时,仅更新节点统计信息。
- 这是
-
process_type[default =default]- 一种运行的助推过程。
- 选择:
default,updatedefault:正常的提升过程,创造新的树木。update:从现有模型开始,仅更新其树。在每次增强迭代中,从初始模型中获取树,为该树运行指定的更新器插件序列,并将修改后的树添加到新模型中。新模型将具有相同或更少数量的树,具体取决于执行的增强迭代次数。目前,以下内置更新程序插件可以有意义地与此进程类型一起使用:refresh,prune. 有了process_type=update,不能使用创建新树的更新程序插件。
-
grow_policy[default =depthwise]- 控制将新节点添加到树中的方式。
- 仅在
tree_method设置为时才支持hist。 - 选择:
depthwise,lossguidedepthwise:在最靠近根的节点处拆分。lossguide:在具有最高损失变化的节点处拆分。
-
max_leaves[默认= 0]- 要添加的最大节点数。仅在
grow_policy=lossguide设置时相关。
- 要添加的最大节点数。仅在
-
max_bin,[默认= 256]- 仅在
tree_method设置为时使用hist。 - 铲斗连续特征的最大离散箱数。
- 增加此数量可以以更高的计算时间为代价提高分割的最佳性。
- 仅在
-
predictor,[default =``cpu_predictor``]- 要使用的预测算法类型。提供相同的结果,但允许使用GPU或CPU。
cpu_predictor:多核CPU预测算法。gpu_predictor:使用GPU进行预测。默认情况下tree_method是gpu_exact或gpu_hist。
- 要使用的预测算法类型。提供相同的结果,但允许使用GPU或CPU。
-
num_parallel_tree,[default = 1] - 每次迭代期间构造的并行树的数量。此选项用于支持增强的随机森林。
Dart Booster(booster=dart)的附加参数
注意
使用predict()DART助推器
如果助推器对象是DART类型,predict()将执行丢失,即仅评估一些树。如果data不是训练数据,这将产生不正确的结果。要在测试集上获得正确的结果,请设置ntree_limit为非零值,例如
preds = bst.predict(dtest, ntree_limit=num_round)
sample_type[default =uniform]- 采样算法的类型。
uniform:统一选择掉落的树木。weighted:根据重量选择落下的树木。
- 采样算法的类型。
normalize_type[default =tree]- 归一化算法的类型。
tree:新树的每棵树都有相同的重量。- 新树的重量是。
1 / (k + learning_rate) - 掉落的树木按比例缩放。
k / (k + learning_rate)
- 新树的重量是。
forest:新树的落叶树木(森林)总重量相同。- 新树的重量是。
1 / (1 + learning_rate) - 掉落的树木按比例缩放。
1 / (1 + learning_rate)
- 新树的重量是。
- 归一化算法的类型。
rate_drop[默认= 0.0]- 辍学率(辍学期间先前树木的一小部分会下降)。
- 范围:[0.0,1.0]
one_drop[默认= 0]- 启用此标志后,在丢失期间始终会丢弃至少一个树(允许从原始DART纸张中进行二项式加1或epsilon-dropout)。
skip_drop[默认= 0.0]- 在增强迭代期间跳过丢失过程的概率。
- 如果跳过了丢失,则以与添加相同的方式添加新树
gbtree。 - 请注意,非零的
skip_drop优先级高于rate_drop或one_drop。
- 如果跳过了丢失,则以与添加相同的方式添加新树
- 范围:[0.0,1.0]
- 在增强迭代期间跳过丢失过程的概率。
Linear Booster(booster=gblinear)的参数
lambda[default = 0,别名:reg_lambda]- 关于权重的L2正则化项。增加此值将使模型更加保守。标准化为训练样本的数量。
alpha[default = 0,别名:reg_alpha]- 关于权重的L1正则化项。增加此值将使模型更加保守。标准化为训练样本的数量。
updater[default =shotgun]- 适合线性模型的算法选择
shotgun:基于鸟枪法的并行坐标下降算法。使用'hogwild'并行性,因此在每次运行时产生一个不确定的解决方案。coord_descent:普通坐标下降算法。也是多线程的,但仍然会产生确定性的解决方案。
- 适合线性模型的算法选择
feature_selector[default =cyclic]- 特征选择和排序方法
cyclic:通过一次循环一个功能确定选择。shuffle:类似于cyclic每次更新之前随机功能改组。random:随机(带替换)坐标选择器。greedy:选择具有最大梯度幅度的坐标。它很O(num_feature^2)复杂。这是完全确定的。它允许top_k通过设置top_k参数将选择限制为具有最大单变量权重变化幅度的每组特征。这样做会降低复杂性O(num_feature*top_k)。thrifty:节俭,近乎贪婪的特征选择器。在循环更新之前,重新排序功能的单变量权重的下降幅度。此操作是多线程的,是二次贪心选择的线性复杂度近似。它允许top_k通过设置top_k参数将选择限制为具有最大单变量权重变化幅度的每组特征。
- 特征选择和排序方法
top_k[默认= 0]- 要选择的顶部要素数
greedy和thrifty要素选择器。值0表示使用所有功能。
- 要选择的顶部要素数
Tweedie回归的参数(objective=reg:tweedie)
tweedie_variance_power[默认= 1.5]- 控制Tweedie分布方差的参数
var(y) ~ E(y)^tweedie_variance_power - 范围:(1,2)
- 设置接近2以转向伽玛分布
- 设置得越接近1,越过泊松分布。
- 控制Tweedie分布方差的参数
学习任务参数
指定学习任务和相应的学习目标。目标选项如下:
objective[默认= REG:squarederror]reg:squarederror:平方损失的回归reg:logistic:逻辑回归binary:logistic:二元分类的逻辑回归,输出概率binary:logitraw:二元分类的逻辑回归,逻辑变换前的输出得分binary:hinge:铰链损失用于二元分类。这使得预测为0或1,而不是产生概率。count:poisson计数数据的泊松回归,泊松分布的输出均值max_delta_step在泊松回归中默认设置为0.7(用于保证优化)
survival:cox:针对右删失生存时间数据的Cox回归(负值被认为是正确的审查)。请注意,预测以风险比例表返回(即,比例风险函数中的HR = exp(marginal_prediction))。h(t) = h0(t) * HRmulti:softmax:设置XGBoost使用softmax目标进行多类分类,还需要设置num_class(类数)multi:softprob:与softmax相同,但输出一个向量,可以进一步重新整形为矩阵。结果包含属于每个类的每个数据点的预测概率。ndata * nclassndata * nclassrank:pairwise:使用LambdaMART执行成对排名,其中成对损失最小化rank:ndcg:使用LambdaMART执行列表方式排名,其中规范化折扣累积增益(NDCG)最大化rank:map:使用LambdaMART执行列表方式排名,其中平均平均精度(MAP)最大化reg:gamma:使用log-link进行gamma回归。输出是伽马分布的平均值。它可能是有用的,例如,用于建模保险索赔严重性,或任何可能是伽玛分布的结果。reg:tweedie:带有日志链接的Tweedie回归。它可能是有用的,例如,用于模拟保险中的总损失,或者可能是Tweedie分布的任何结果。
base_score[默认= 0.5]- 所有实例的初始预测分数,全球偏差
- 对于足够数量的迭代,更改此值不会产生太大影响。
eval_metric[根据目标默认]- 验证数据的评估指标,将根据目标分配默认指标(回归的rmse和分类的误差,排名的平均平均精度)
- 用户可以添加多个评估指标。Python用户:记得将指标作为参数对列表而不是map传递,以便后者
eval_metric不会覆盖前一个 - 选项如下:
rmse:均方根误差mae:平均绝对误差logloss:负对数似然error:二进制分类错误率。它的计算方法是。对于预测,评估将具有大于0.5的预测值的实例视为正实例,而将其他实例视为负实例。#(wrong cases)/#(all cases)error@t:通过't'提供数值,可以指定不同于0.5的二进制分类阈值。merror:多类分类错误率。它的计算方法是。#(wrong cases)/#(all cases)mlogloss:多类logloss。auc:曲线下面积aucpr:PR曲线下面积ndcg:标准化折扣累积增益map:平均平均精度ndcg@n,map@n:'n'可以指定为整数,以切断列表中的顶部位置以进行评估。ndcg-,map-,ndcg@n-,map@n-:在XGBoost,NDCG和MAP将评估清单的比分没有任何阳性样品为1加入-在评价指标XGBoost将评估这些得分为0,是在一定条件下一致“”。poisson-nloglik:泊松回归的负对数似然gamma-nloglik:伽马回归的负对数似然cox-nloglik:Cox比例风险回归的负部分对数似然gamma-deviance:伽马回归的剩余偏差tweedie-nloglik:Tweedie回归的负对数似然(在tweedie_variance_power参数的指定值处)
seed[默认= 0]- 随机数种子。
命令行参数
以下参数仅用于XGBoost的控制台版本
num_round- 提升的轮次数
data- 培训数据的路径
test:data- 测试数据的路径做预测
save_period[默认= 0]- 保存模型的时间段。设置
save_period=10意味着每10轮XGBoost将保存模型。将其设置为0表示在培训期间不保存任何模型。
- 保存模型的时间段。设置
task[默认=train]选项:train,pred,eval,dumptrain:使用数据进行培训pred:预测测试:数据eval:用于评估指定的统计信息eval[name]=filenamedump:用于将学习的模型转储为文本格式
model_in[默认= NULL]- 路径输入模型,需要的
test,eval,dump任务。如果在训练中指定,XGBoost将继续从输入模型进行训练。
- 路径输入模型,需要的
model_out[默认= NULL]- 训练结束后输出模型的路径。如果未指定,XGBoost将输出具有诸如增强轮数的
0003.model位置的文件0003。
- 训练结束后输出模型的路径。如果未指定,XGBoost将输出具有诸如增强轮数的
model_dir[default =models/]- 训练期间保存模型的输出目录
fmap- 特征映射,用于转储模型
dump_format[default =text]选项:text,json- 模型转储文件的格式
name_dump[default =dump.txt]- 模型转储文件的名称
name_pred[default =pred.txt]- 预测文件的名称,用于pred模式
pred_margin[默认= 0]- 预测保证金而不是转换概率

 的对应目标函数的
的对应目标函数的 ,
,

 浙公网安备 33010602011771号
浙公网安备 33010602011771号