BUAA-OO-2021-第一单元总结
OO第一单元总结
随着大二生活的第一个月走近尾声,OO的第一单元也结束了,第一单元有三次作业,分别为:多项式求导,带有幂函数、三角函数的表达式求导 和 带嵌套的表达式求导。下面我将从程序结构的分析入手,对本次作业进行总结。
程序结构分析
第一次作业
- UML类图
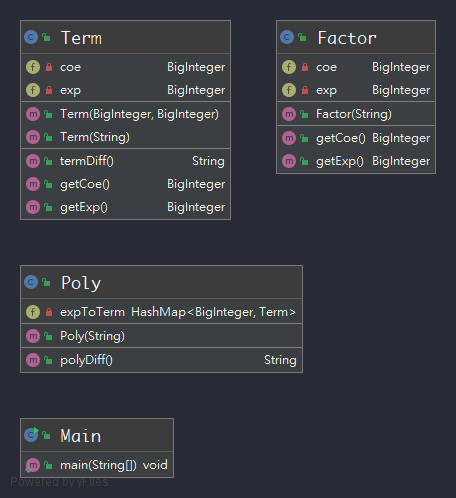
可以看出第一次的程序结构非常简单,大概就是建立多项式、项、因子三个类,因为此次作业的因子都能用常数*幂函数的形式表示,所以就用了一个factor类概括,此处还有一个小技巧就是将constructor当做parser来用,利用正则表达式在poly中查找term,term中查找factor进行解析。
- 方法复杂度分析
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Factor.Factor(String) | 12 | 1 | 6 | 6 |
| Factor.getCoe() | 0 | 1 | 1 | 1 |
| Factor.getExp() | 0 | 1 | 1 | 1 |
| Main.main(String[]) | 0 | 1 | 1 | 1 |
| Poly.Poly(String) | 7 | 1 | 4 | 4 |
| Poly.polyDiff() | 6 | 1 | 3 | 5 |
| Term.Term(BigInteger,BigInteger) | 0 | 1 | 1 | 1 |
| Term.Term(String) | 4 | 1 | 4 | 4 |
| Term.getCoe() | 0 | 1 | 1 | 1 |
| Term.getExp() | 0 | 1 | 1 | 1 |
| Term.termDiff() | 3 | 3 | 3 | 3 |
| TermHashMap.getTermHashMap() | 0 | 1 | 1 | 1 |
| TermHashMap.polyDiff() | 0 | 1 | 1 | 1 |
发现某些构造函数的复杂度较高,初步推断是因为本次作业没有wrong format的情况,有很多if都只考虑了符合条件的情况,而没写else导致的。
-
耦合度
Class OCavg OCmax WMC Factor 2.67 6 8 Main 1 1 1 Poly 4.5 5 9 Term 2 4 10 TermHashMap 1 1 2
第二次作业
-
UML类图
![H2UML]()
-
第二次作业由于引入了sin、cos和多项式作为一个因子,显然利用一个因子类是难以储存这么多信息的,因此笔者将Factor写成一个抽象类再从中继承了如图所示的五种因子,并利用了工厂模式来创建因子。
-
在多项式的解析中,仍然沿用了第一次利用正则一层一层查找的思路,一个巧妙之处在于利用压栈将polyFactor的所有小括号换成了中括号,使正则匹配不存在递归调用的情形
(也是为什么大家都用递归下降的时候我能继续正则匹配),但在写这个polyStandardize函数时没想好就把它装在了Main里面,这无疑是太面向过程了。 -
本次作业同样因为没有wrong format的判定,写代码时都只考虑符合情况的条件,而没写很多else,尤其体现在上述压栈的过程中导致圈复杂度过高。
- 方法复杂度分析
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Constant.Constant(BigInteger) | 0 | 1 | 1 | 1 |
| Constant.Constant(String) | 3 | 1 | 3 | 3 |
| Constant.getCoe() | 0 | 1 | 1 | 1 |
| Constant.getDerivation() | 0 | 1 | 1 | 1 |
| Constant.toString() | 2 | 2 | 2 | 2 |
| Cos.Cos(BigInteger) | 0 | 1 | 1 | 1 |
| Cos.Cos(String) | 4 | 1 | 3 | 3 |
| Cos.getDerivation() | 3 | 1 | 3 | 3 |
| Cos.getExp() | 0 | 1 | 1 | 1 |
| Cos.toString() | 3 | 3 | 3 | 3 |
| FactorFactory.getFactor(String) | 5 | 6 | 1 | 6 |
| Main.main(String[]) | 0 | 1 | 1 | 1 |
| Main.outputStandardize(Poly) | 4 | 2 | 3 | 4 |
| Main.polyStandardize(String) | 21 | 7 | 7 | 12 |
| Poly.Poly(ArrayList |
0 | 1 | 1 | 1 |
| Poly.Poly(String) | 4 | 1 | 4 | 4 |
| Poly.getDerivation() | 1 | 1 | 2 | 2 |
| Poly.getTermArrayList() | 0 | 1 | 1 | 1 |
| Poly.toString() | 9 | 5 | 3 | 6 |
| Power.Power(BigInteger) | 0 | 1 | 1 | 1 |
| Power.Power(String) | 4 | 1 | 3 | 3 |
| Power.getDerivation() | 2 | 1 | 3 | 3 |
| Power.getExp() | 0 | 1 | 1 | 1 |
| Power.toString() | 3 | 3 | 3 | 3 |
| Sin.Sin(BigInteger) | 0 | 1 | 1 | 1 |
| Sin.Sin(String) | 4 | 1 | 3 | 3 |
| Sin.getDerivation() | 3 | 1 | 3 | 3 |
| Sin.getExp() | 0 | 1 | 1 | 1 |
| Sin.toString() | 3 | 3 | 3 | 3 |
| Term.Term(ArrayList |
0 | 1 | 1 | 1 |
| Term.Term(String) | 3 | 1 | 3 | 3 |
| Term.getDerivation() | 6 | 1 | 4 | 4 |
| Term.mergeFactors() | 7 | 1 | 7 | 7 |
| Term.toString() | 12 | 6 | 3 | 6 |
-
耦合度分析
Class OCavg OCmax WMC Constant 1.6 3 8 Cos 2.2 3 11 Factor n/a n/a 0 FactorFactory 6 6 6 Main 3.67 7 11 Poly 2.8 6 14 Power 2.2 3 11 Sin 2.2 3 11 Term 4.2 7 21
第三次作业
-
UML类图
![H3UML]() )
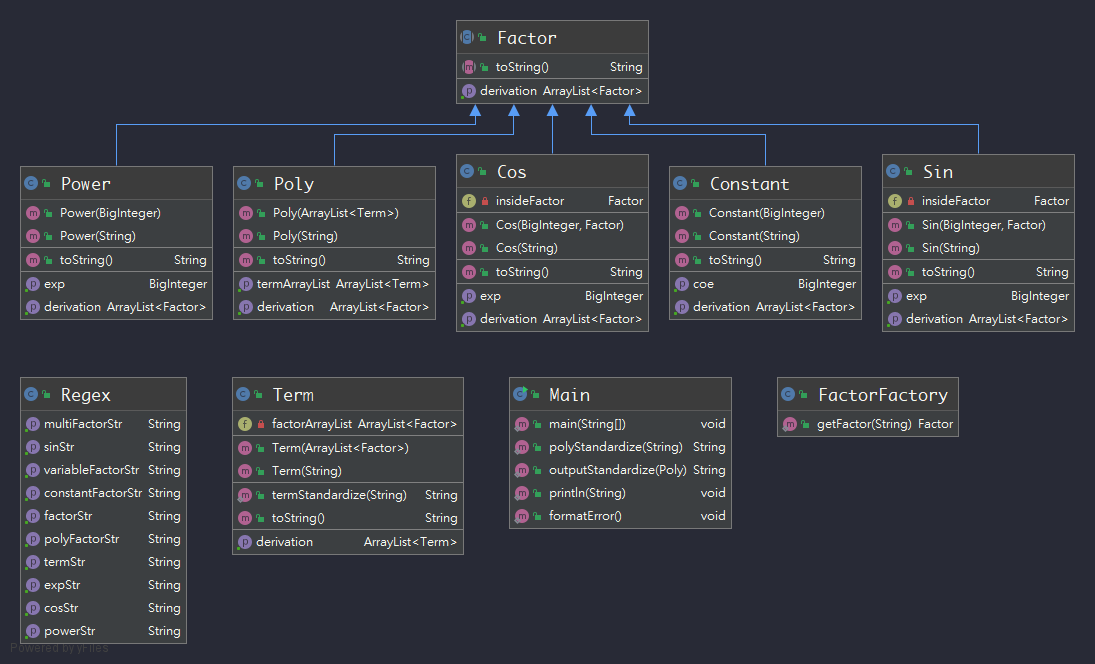
)本次作业和第二次采用的架构几乎相同,不同的是经过思考,笔者发现再用正则依次自顶向下匹配的方法因为嵌套过多即使可行实现起来也过于麻烦,只得采用比较纯粹的递归下降的解析方法,大概思路就是扫一遍传进去的字符串利用[+-]将poly分成term,利用*将term分成factor(**先replace成^),其余的如类的继承关系以及求导的方法等都没有大的改动。
再看看本次的复杂度和耦合度确实有点惨不忍睹,究其原因无疑是在扫描解析poly和term的时候进行了过多的if特判来找出wrong format(导致圈复杂度过高),同时两者扫描的过程也有很多复用的代码(导致耦合度过高),虽然最后写出来了代码,但是代码笔者自己读起来都有些恶心。
-
方法复杂度分析
Method CogC ev(G) iv(G) v(G) Constant.Constant(BigInteger) 0 1 1 1 Constant.Constant(String) 3 1 3 3 Constant.getCoe() 0 1 1 1 Constant.getDerivation() 0 1 1 1 Constant.toString() 0 1 1 1 Cos.Cos(BigInteger,Factor) 0 1 1 1 Cos.Cos(String) 7 1 4 5 Cos.getDerivation() 3 1 3 3 Cos.getExp() 0 1 1 1 Cos.toString() 3 3 3 3 FactorFactory.getFactor(String) 5 6 3 6 Main.formatError() 0 1 1 1 Main.main(String[]) 0 1 1 1 Main.outputStandardize(Poly) 4 2 3 4 Main.polyStandardize(String) 4 1 5 5 Main.println(String) 0 1 1 1 Poly.Poly(ArrayList ) 0 1 1 1 Poly.Poly(String) 22 1 15 17 Poly.getDerivation() 1 1 2 2 Poly.getTermArrayList() 0 1 1 1 Poly.toString() 8 4 2 5 Power.Power(BigInteger) 0 1 1 1 Power.Power(String) 6 1 4 5 Power.getDerivation() 2 1 3 3 Power.getExp() 0 1 1 1 Power.toString() 3 3 3 3 Regex.getConstantFactorStr() 0 1 1 1 Regex.getCosStr() 0 1 1 1 Regex.getExpStr() 0 1 1 1 Regex.getFactorStr() 0 1 1 1 Regex.getMultiFactorStr() 0 1 1 1 Regex.getPolyFactorStr() 0 1 1 1 Regex.getPowerStr() 0 1 1 1 Regex.getSinStr() 0 1 1 1 Regex.getTermStr() 0 1 1 1 Regex.getVariableFactorStr() 0 1 1 1 Sin.Sin(BigInteger,Factor) 0 1 1 1 Sin.Sin(String) 7 1 4 5 Sin.getDerivation() 3 1 3 3 Sin.getExp() 0 1 1 1 Sin.toString() 3 3 3 3 Term.Term(ArrayList ) 0 1 1 1 Term.Term(String) 26 1 13 14 Term.getDerivation() 6 1 4 4 Term.termStandardize(String) 12 4 9 10 Term.toString() 12 6 3 6 -
耦合度分析
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| Constant | 1.4 | 3 | 7 |
| Cos | 2.4 | 4 | 12 |
| Factor | n/a | n/a | 0 |
| FactorFactory | 6 | 6 | 6 |
| Main | 2 | 4 | 10 |
| Poly | 4 | 11 | 20 |
| Power | 2.4 | 4 | 12 |
| Regex | 1 | 1 | 10 |
| Sin | 2.4 | 4 | 12 |
| Term | 6.4 | 13 | 32 |
Bug分析
-
第一次作业
第一次作业强测和互测中出现的都是一个shared bug,是因为没有认真研读指导书正则表达式写错了(允许前导零的整数的重复个数),在测试的时候发现了问题,前面写错的代码改了,而后面复用的正则表达式却没改导致的。
解决:
"[0-9]{0,9}" -> "[0-9]*" -
第二次作业
第二次作业强测和互测中出现的问题是输出时的toString多次复用导致的TLE。
解决:
String termString = term.toString(); //使用时避免多次调用toString -
第三次作业
第三次作业有两个bug,一个是没有对poly括号中是空串的情况进行wrong format特判,另一个是判断不是数字的时候本应是
x<0 && x>9而写成了x<=0 && x>=9(本来进行简单的边界测试应该就能测出来)
发现bug的策略
- 首先无疑根据指导书将自己遇到的一些坑点造成数据来测别人的程序,如边界数据、常数组合等。
- 其次还可以通读别人的代码发现一些漏洞,当然通读也是有选择性的找输入输出的部分以提高效率。
- 自动化测试,通过测评机跑大量的数据来发现bug,但由于笔者并没有完成完整的测评机,在此不做过多评价。
重构
本单元的三次作业可以说每次作业都多多少少经历了重构这一步,其中第二次作业是最痛苦的,引入了三角和嵌套,除了继承了一点第一次自顶向下解析的思想其他的什么存储信息、求导、输出过程都经历了重构,而第三次作业反而比较轻松,求导和toString输出简单的改动就能满足第三次作业的功能,比较痛苦的是parse的过程,笔者程序的架构过差,为了涵盖所有的wrong format加入了太多特判。
心得体会
第一单元的三次作业带我们第一次经历了迭代开发一个系统的java项目,让我们逐渐完成了从c语言的面向过程的思维到面向对象的思维转变,这三周的设计也让我充分意识到迭代式设计一定要为代码建立良好的可拓展性,不能想到一点写一点,整体的架构是一个项目的重中之重。
总的来说,这三周虽然较为忙碌,但在老师和助教的悉心指导下还算得上收获满满,在接下来的OO课程中,希望我能继续努力,持续提高自己面向对象设计的能力。



 )
)
 浙公网安备 33010602011771号
浙公网安备 33010602011771号