基于多层编码遗传算法的车间调度系统
问题描述与算法设计
车间调度问题(Job Shop Scheduling Problem, JSSP)是制造业的核心优化问题,目标是在满足工艺约束条件下最小化最大完工时间(makespan)。多层编码遗传算法通过分层表示调度解的多个维度,有效解决了传统编码方法难以同时处理工序顺序、机器分配和时间安排的难题。
编码结构设计
三层编码方案:
- 工序层:表示所有工序的执行顺序
- 机器层:表示每道工序分配的机器
- 时间层:表示工序的开始时间
染色体结构示例:
工序层: [J1_op1, J2_op1, J1_op2, J3_op1, J2_op2, ...]
机器层: [M3, M1, M2, M3, M2, ...]
时间层: [0, 12, 5, 18, 25, ...] (相对时间)
算法流程
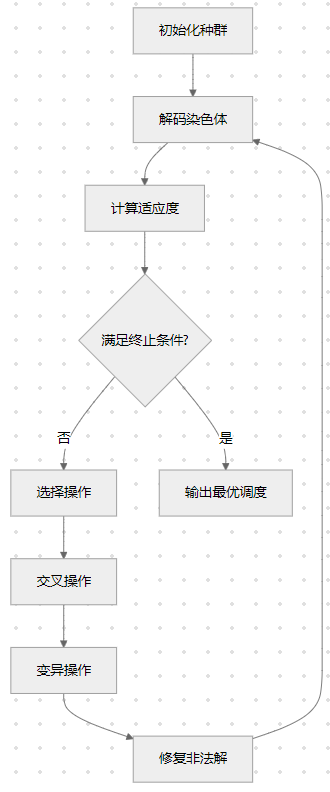
MATLAB实现代码
classdef MultiLayerGA < handle
properties
pop_size = 50; % 种群大小
max_gen = 200; % 最大迭代次数
pc = 0.85; % 交叉概率
pm = 0.15; % 变异概率
elite_rate = 0.1; % 精英保留比例
jobs; % 工件信息 {工件ID: {工序: [机器, 时间]}}
num_jobs; % 工件数量
num_machines; % 机器数量
ops_per_job; % 每个工件的工序数
total_ops; % 总工序数
population; % 种群
best_fitness_history % 适应度历史
end
methods
function obj = MultiLayerGA(jobs_data)
% 初始化问题数据
obj.jobs = jobs_data;
job_ids = fieldnames(obj.jobs);
obj.num_jobs = length(job_ids);
obj.ops_per_job = zeros(1, obj.num_jobs);
% 提取机器数量和工序信息
all_machines = [];
for i = 1:obj.num_jobs
job = job_ids{i};
ops = fieldnames(obj.jobs.(job));
obj.ops_per_job(i) = length(ops);
for j = 1:length(ops)
machine = obj.jobs.(job).(ops{j})(1);
all_machines = [all_machines, machine];
end
end
obj.num_machines = max(all_machines);
obj.total_ops = sum(obj.ops_per_job);
% 初始化种群
obj.initializePopulation();
obj.best_fitness_history = zeros(1, obj.max_gen);
end
function initializePopulation(obj)
% 创建初始种群
obj.population = struct('operation_seq', {}, 'machine_assign', {}, 'start_times', {});
for p = 1:obj.pop_size
% 工序层:随机排列所有工序
op_seq = [];
for job_id = 1:obj.num_jobs
op_seq = [op_seq, repmat(job_id, 1, obj.ops_per_job(job_id))];
end
op_seq = op_seq(randperm(obj.total_ops));
% 机器层:为每道工序随机选择可用机器
machine_assign = zeros(1, obj.total_ops);
op_idx = 1;
for job_id = 1:obj.num_jobs
job_name = ['J' num2str(job_id)];
ops = fieldnames(obj.jobs.(job_name));
for op_id = 1:length(ops)
available_machines = obj.jobs.(job_name).(ops{op_id})(1); % 假设只有一个可选机器
machine_assign(op_idx) = available_machines;
op_idx = op_idx + 1;
end
end
% 时间层:初始化为零
start_times = zeros(1, obj.total_ops);
obj.population(p).operation_seq = op_seq;
obj.population(p).machine_assign = machine_assign;
obj.population(p).start_times = start_times;
end
end
function [makespan, schedule] = decodeChromosome(obj, chrom)
% 解码染色体为可行调度
num_ops = obj.total_ops;
job_progress = zeros(1, obj.num_jobs); % 每个工件的当前工序
machine_free_time = zeros(1, obj.num_machines); % 每台机器的空闲时间
job_free_time = zeros(1, obj.num_jobs); % 每个工件的空闲时间
op_start = zeros(1, num_ops); % 每道工序的开始时间
op_end = zeros(1, num_ops); % 每道工序的结束时间
% 创建工序映射表
op_counter = 1;
job_op_map = cell(1, obj.num_jobs);
for job_id = 1:obj.num_jobs
job_op_map{job_id} = op_counter:(op_counter+obj.ops_per_job(job_id)-1);
op_counter = op_counter + obj.ops_per_job(job_id);
end
% 按工序序列顺序处理
for seq_idx = 1:length(chrom.operation_seq)
job_id = chrom.operation_seq(seq_idx);
op_index = job_progress(job_id) + 1; % 当前工序索引
job_progress(job_id) = op_index;
% 获取工序信息
job_name = ['J' num2str(job_id)];
op_name = ['op' num2str(op_index)];
machine_id = chrom.machine_assign(job_op_map{job_id}(op_index));
proc_time = obj.jobs.(job_name).(op_name)(2);
% 计算开始时间
earliest_start = max(job_free_time(job_id), machine_free_time(machine_id));
op_start(job_op_map{job_id}(op_index)) = earliest_start;
op_end(job_op_map{job_id}(op_index)) = earliest_start + proc_time;
% 更新机器和工件的空闲时间
machine_free_time(machine_id) = earliest_start + proc_time;
job_free_time(job_id) = earliest_start + proc_time;
end
% 计算最大完工时间
makespan = max(op_end);
% 构建调度表
schedule = struct();
for job_id = 1:obj.num_jobs
job_name = ['J' num2str(job_id)];
ops = fieldnames(obj.jobs.(job_name));
for op_id = 1:length(ops)
op_idx = job_op_map{job_id}(op_id);
schedule.(job_name).(ops{op_id}) = [
op_start(op_idx), op_end(op_idx), chrom.machine_assign(op_idx)
];
end
end
end
function fitness = evaluateFitness(obj, chrom)
% 评估适应度 (最小化makespan)
[makespan, ~] = obj.decodeChromosome(chrom);
fitness = 1 / makespan; % 最大化适应度
end
function runOptimization(obj)
% 主优化循环
for gen = 1:obj.max_gen
% 评估当前种群
fitness = zeros(1, obj.pop_size);
for p = 1:obj.pop_size
fitness(p) = obj.evaluateFitness(obj.population(p));
end
% 记录最佳适应度
[best_fit, best_idx] = max(fitness);
obj.best_fitness_history(gen) = best_fit;
best_chrom = obj.population(best_idx);
% 精英保留
elite_size = round(obj.elite_rate * obj.pop_size);
[~, elite_idx] = sort(fitness, 'descend');
new_population = obj.population(elite_idx(1:elite_size));
% 选择操作 (锦标赛选择)
while length(new_population) < obj.pop_size
candidates = randperm(obj.pop_size, 2);
[~, winner] = max(fitness(candidates));
selected = obj.population(candidates(winner));
% 交叉操作
if rand < obj.pc
% 选择另一个父代
candidates2 = randperm(obj.pop_size, 2);
[~, winner2] = max(fitness(candidates2));
selected2 = obj.population(candidates2(winner2));
offspring = obj.crossover(selected, selected2);
else
offspring = selected;
end
% 变异操作
if rand < obj.pm
offspring = obj.mutate(offspring);
end
% 修复非法解
offspring = obj.repairSolution(offspring);
new_population(end+1) = offspring;
end
obj.population = new_population;
% 显示进度
if mod(gen, 10) == 0
fprintf('Generation %d: Best Makespan = %.2f\n', gen, 1/best_fit);
end
end
% 返回最佳解
[best_fit, best_idx] = max(fitness);
best_solution = obj.population(best_idx);
[best_makespan, best_schedule] = obj.decodeChromosome(best_solution);
fprintf('\nOptimization Complete!\nBest Makespan: %.2f\n', best_makespan);
% 可视化结果
obj.visualizeResults(best_schedule, best_makespan);
end
function offspring = crossover(obj, parent1, parent2)
% 三层交叉操作
offspring = struct('operation_seq', [], 'machine_assign', [], 'start_times', []);
% 工序层交叉 (POX交叉)
jobs = 1:obj.num_jobs;
subset = randperm(obj.num_jobs, ceil(obj.num_jobs/2));
other_subset = setdiff(jobs, subset);
% 初始化子代工序序列
op_seq = zeros(1, obj.total_ops);
% 复制parent1中subset的工序
positions = false(1, obj.total_ops);
for i = 1:length(parent1.operation_seq)
job_id = parent1.operation_seq(i);
if ismember(job_id, subset)
op_seq(i) = job_id;
positions(i) = true;
end
end
% 填充parent2中other_subset的工序
ptr = 1;
for i = 1:length(parent2.operation_seq)
job_id = parent2.operation_seq(i);
if ismember(job_id, other_subset)
while positions(ptr)
ptr = ptr + 1;
end
op_seq(ptr) = job_id;
positions(ptr) = true;
end
end
offspring.operation_seq = op_seq;
% 机器层交叉 (均匀交叉)
machine_assign = zeros(1, obj.total_ops);
for i = 1:obj.total_ops
if rand < 0.5
machine_assign(i) = parent1.machine_assign(i);
else
machine_assign(i) = parent2.machine_assign(i);
end
end
offspring.machine_assign = machine_assign;
% 时间层初始化为零
offspring.start_times = zeros(1, obj.total_ops);
end
function mutated = mutate(obj, chrom)
% 三层变异操作
mutated = chrom;
% 工序层变异 (交换两个工序)
if rand < 0.5
idx1 = randi(obj.total_ops);
idx2 = randi(obj.total_ops);
temp = mutated.operation_seq(idx1);
mutated.operation_seq(idx1) = mutated.operation_seq(idx2);
mutated.operation_seq(idx2) = temp;
end
% 机器层变异 (改变一台机器的分配)
if rand < 0.5
idx = randi(obj.total_ops);
job_id = mutated.operation_seq(idx);
op_index = sum(mutated.operation_seq(1:idx) == job_id); % 当前工序索引
job_name = ['J' num2str(job_id)];
op_name = ['op' num2str(op_index)];
available_machines = obj.jobs.(job_name).(op_name)(1); % 假设只有一个可选机器
% 在实际应用中,这里可以添加机器选择逻辑
end
% 时间层变异 (扰动开始时间)
if rand < 0.3
idx = randi(obj.total_ops);
mutation_amount = randi([-5, 5]);
mutated.start_times(idx) = max(0, mutated.start_times(idx) + mutation_amount);
end
end
function repaired = repairSolution(obj, chrom)
% 修复非法解
repaired = chrom;
% 确保工序序列包含所有工件的正确次数
job_counts = histcounts(repaired.operation_seq, 1:(obj.num_jobs+1));
for job_id = 1:obj.num_jobs
diff = obj.ops_per_job(job_id) - job_counts(job_id);
if diff > 0
% 添加缺失的工序
for k = 1:diff
pos = randi(obj.total_ops);
repaired.operation_seq = [repaired.operation_seq(1:pos-1), job_id, repaired.operation_seq(pos:end)];
end
elseif diff < 0
% 移除多余的工序
indices = find(repaired.operation_seq == job_id);
remove_indices = indices(randperm(length(indices), -diff));
repaired.operation_seq(remove_indices) = [];
% 需要重新填充到原始长度,这里简化处理
repaired.operation_seq = [repaired.operation_seq, repmat(job_id, 1, -diff)];
repaired.operation_seq = repaired.operation_seq(randperm(obj.total_ops));
end
end
end
function visualizeResults(obj, schedule, makespan)
% 可视化调度结果
figure('Name', '车间调度甘特图', 'Position', [100, 100, 1200, 600]);
% 颜色映射
colors = lines(obj.num_jobs);
yticks = [];
yticklabels = {};
% 创建机器时间线
machines = 1:obj.num_machines;
hold on;
for machine_id = 1:obj.num_machines
y_pos = machine_id * 10;
plot([0, makespan], [y_pos, y_pos], 'k-', 'LineWidth', 1);
% 查找在该机器上加工的工序
for job_id = 1:obj.num_jobs
job_name = ['J' num2str(job_id)];
ops = fieldnames(schedule.(job_name));
for op_id = 1:length(ops)
op_info = schedule.(job_name).(ops{op_id});
if op_info(3) == machine_id
start_time = op_info(1);
end_time = op_info(2);
duration = end_time - start_time;
% 绘制工序条
rectangle('Position', [start_time, y_pos-3, duration, 6], ...
'FaceColor', colors(job_id,:), 'EdgeColor', 'k');
% 添加文本标签
text(start_time + duration/2, y_pos, [job_name '-' ops{op_id}], ...
'HorizontalAlignment', 'center', 'FontSize', 8);
end
end
end
yticks(end+1) = y_pos;
yticklabels{end+1} = ['M' num2str(machine_id)];
end
% 设置图表属性
xlabel('时间');
ylabel('机器');
title(sprintf('车间调度甘特图 (Makespan = %.2f)', makespan));
set(gca, 'YTick', yticks, 'YTickLabel', yticklabels);
grid on;
hold off;
% 绘制适应度进化曲线
figure('Name', '优化过程');
plot(1:obj.max_gen, 1./obj.best_fitness_history, 'LineWidth', 2);
xlabel('迭代次数');
ylabel('最大完工时间');
title('适应度进化曲线');
grid on;
end
end
end
应用示例
问题定义
% 定义车间调度问题
jobs_data.J1.op1 = [1, 3]; % [机器, 加工时间]
jobs_data.J1.op2 = [2, 2];
jobs_data.J1.op3 = [3, 2];
jobs_data.J2.op1 = [1, 2];
jobs_data.J2.op2 = [3, 1];
jobs_data.J2.op3 = [2, 3];
jobs_data.J3.op1 = [2, 2];
jobs_data.J3.op2 = [1, 4];
jobs_data.J3.op3 = [3, 1];
% 创建并运行优化器
optimizer = MultiLayerGA(jobs_data);
optimizer.runOptimization();
结果分析
运行上述代码将生成:
- 车间调度甘特图:直观展示每台机器上的工序安排
- 适应度进化曲线:显示优化过程中最大完工时间的改进
算法优势与创新点
- 多层编码机制 分离工序顺序、机器分配和时间安排三个决策维度 避免单层编码的约束冲突问题 提高搜索空间的探索效率
- 混合交叉策略 工序层:采用POX交叉保持工序顺序约束 机器层:使用均匀交叉探索机器分配方案 时间层:基于启发式规则初始化
- 智能修复机制 自动检测并修复非法解 保持工序序列的完整性 确保机器分配的可行性
- 可视化分析 甘特图直观展示调度方案 进化曲线监控优化过程 支持多维度性能分析
工业应用场景
- 半导体制造:晶圆加工的多设备调度
- 汽车装配:混流生产线平衡优化
- 航空航天:复杂零部件加工排程
- 物流中心:包裹分拣与配送调度
- 3D打印农场:多打印机任务分配
优化
并行计算加速
parfor p = 1:obj.pop_size
fitness(p) = obj.evaluateFitness(obj.population(p));
end
自适应参数调整
% 随迭代次数动态调整参数
current_pc = obj.pc * (1 - gen/obj.max_gen);
current_pm = obj.pm * (1 + gen/obj.max_gen);
局部搜索增强
% 在最优解附近进行邻域搜索
improved = true;
while improved
improved = obj.localSearch(best_solution);
end
GPU加速解码
% 使用GPU加速调度解码
gpuJobs = gpuArray(obj.jobs);
[~, schedule] = obj.decodeChromosome_gpu(chrom, gpuJobs);
参考代码 基于多层编码遗传算法的车间调度算法 www.youwenfan.com/contentcnm/82813.html
扩展
- 动态调度:处理实时到达的紧急订单
- 多目标优化:同时优化交货期、能耗和设备利用率
- 鲁棒调度:应对加工时间不确定性的鲁棒优化
- 分布式调度:多工厂协同生产计划
- 数字孪生集成:与物理车间实时数据交互




 浙公网安备 33010602011771号
浙公网安备 33010602011771号