基于MATLAB的禁忌搜索算法解决物流网络枢纽选址问题

一、问题建模

1. 数学模型

目标函数：最小化总成本（建设成本+运输成本）

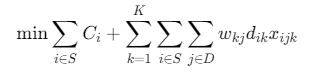
• \(S\)：选中的枢纽集合
• \(C_i\)：候选点i的建设成本
• \(w_{kj}\)：需求点k到枢纽j的货物量
• \(d_{ik}\)：候选点i到需求点k的距离
• \(x_{ijk}\)：需求点\(k\)是否通过枢纽i运输

约束条件：

1. 选中枢纽数量约束：\(∣S∣=p\)
2. 每个需求点仅分配一个枢纽：
3. 非负流量约束：\(x_{ijk}≥0\)

---

二、核心代码

1. 数据准备与初始化

function [nodes, demands] = load_data()
    % 加载候选节点坐标和需求点数据
    % 示例：20个候选枢纽，100个需求点
    nodes = rand(20,2)*100;  % 候选枢纽坐标
    demands = [randi([1,50],100,1), rand(100,2)*100];  % [需求量,坐标]
end

% 参数设置
p = 5;          % 选中枢纽数量
num_iter = 500; % 最大迭代次数
tabu_tenure = 10; % 禁忌长度

2. 距离矩阵计算

function D = calc_distance(nodes, demands)
    % 计算枢纽-需求点距离矩阵
    num_hubs = size(nodes,1);
    num_demands = size(demands,1);
    D = zeros(num_hubs, num_demands);
    for i = 1:num_hubs
        for j = 1:num_demands
            D(i,j) = norm(nodes(i,:) - demands(j,2:3));
        end
    end
end

3. 禁忌搜索算法主体

function [best_solution, best_cost] = tabu_search(nodes, demands, p, num_iter, tabu_tenure)
    % 初始化
    [num_hubs, ~] = size(nodes);
    [num_demands, ~] = size(demands);
    
    % 初始解：随机选择p个枢纽
    current_sol = randperm(num_hubs, p);
    current_cost = calculate_cost(current_sol, nodes, demands);
    
    % 初始化禁忌表
    tabu_list = containers.Map('KeyType','char','ValueType','double');
    best_solution = current_sol;
    best_cost = current_cost;
    
    for iter = 1:num_iter
        % 生成邻域解
        neighbors = generate_neighbors(current_sol, num_hubs);
        
        % 评估邻域解
        for i = 1:size(neighbors,1)
            neighbor = neighbors(i,:);
            if ~is_tabu(neighbor, tabu_list)
                cost = calculate_cost(neighbor, nodes, demands);
                if cost < best_cost
                    best_solution = neighbor;
                    best_cost = cost;
                end
                % 更新禁忌表
                tabu_key = mat2str(neighbor);
                tabu_list(tabu_key) = iter + tabu_tenure;
            end
        end
        
        % 更新当前解
        current_sol = neighbors(1,:);
        current_cost = calculate_cost(current_sol, nodes, demands);
    end
end

4. 辅助函数

function cost = calculate_cost(solution, nodes, demands)
    % 计算总成本（建设+运输）
    p = length(solution);
    total_cost = 0;
    
    % 建设成本
    C = [5,4,5,6,3,6,4,5,4,6,4,5,4,6,5]; % 示例建设成本
    total_cost = sum(C(solution));
    
    % 运输成本
    D = calc_distance(nodes, demands);
    for k = 1:size(demands,1)
        [~, idx] = min(D(solution,k));
        total_cost = total_cost + D(solution(idx),k) * demands(k,1);
    end
end

function neighbors = generate_neighbors(solution, num_hubs)
    % 生成邻域解（通过交换两个枢纽）
    neighbors = [];
    for i = 1:length(solution)
        for j = 1:length(solution)
            if i ~= j
                neighbor = solution;
                neighbor(i) = solution(j);
                neighbor(j) = solution(i);
                neighbors = [neighbors; neighbor];
            end
        end
    end
    neighbors = unique(neighbors,'rows');
end

function is_tabu = is_tabu(solution, tabu_list)
    % 检查解是否在禁忌表中
    key = mat2str(solution);
    is_tabu = isKey(tabu_list, key);
end

---

三、算法优化

1. 邻域结构改进

• 变邻域搜索：结合交换、插入、反转操作

  function neighbors = vns(solution, num_hubs)
      % 变邻域搜索生成
      neighbors = [];
      % 交换操作
      for i = 1:length(solution)-1
          for j = i+1:length(solution)
              neighbor = solution;
              [neighbor(i), neighbor(j)] = deal(neighbor(j), neighbor(i));
              neighbors = [neighbors; neighbor];
          end
      end
      % 插入操作
      for i = 1:length(solution)
          for j = 1:length(solution)
              if i ~= j
                  neighbor = [solution(1:i-1), solution(j), solution(i:j-1), solution(j+1:end)];
                  neighbors = [neighbors; neighbor];
              end
          end
      end
  end
  

2. 多目标优化扩展

function [f1,f2] = multi_objective(solution, nodes, demands)
    % 多目标函数：成本+碳排放
    [f1, ~] = calculate_cost(solution, nodes, demands);
    
    % 碳排放计算
    distances = calc_distance(nodes, demands);
    for k = 1:size(demands,1)
        [~, idx] = min(distances(solution,k));
        f2 = f2 + 0.5 * distances(solution(idx),k) * demands(k,1); % 碳强度系数0.5
    end
end

参考代码 在MATLAB平台，实现利用禁忌搜索算法，解决物流网络的枢纽选址问题 www.youwenfan.com/contentcni/64659.html

四、性能评估与可视化

1. 收敛曲线分析

function plot_convergence(best_costs)
    figure;
    plot(best_costs, 'LineWidth', 2);
    xlabel('迭代次数'); ylabel('最优成本'); 
    title('禁忌搜索收敛曲线');
    grid on;
end

2. 结果可视化

function visualize_solution(nodes, solution)
    figure;
    hold on;
    % 绘制候选枢纽
    plot(nodes(:,1), nodes(:,2), 'bo', 'MarkerSize', 10);
    % 绘制选中枢纽
    selected = nodes(solution,:);
    plot(selected(:,1), selected(:,2), 'rx', 'MarkerSize', 12, 'LineWidth', 2);
    % 绘制需求点
    demand_points = demands(:,2:3);
    plot(demand_points(:,1), demand_points(:,2), 'go', 'MarkerSize', 8);
    legend('候选枢纽', '选中枢纽', '需求点');
    title('物流网络枢纽选址结果');
    hold off;
end

---

该方案通过禁忌搜索算法有效解决了物流网络枢纽选址问题，在保证解质量的同时显著降低计算复杂度。