week3题解

1.寄包柜

 

 

 看到题目最容易想到开二位数组

但数据量过大，因此需要map

#include <bits/stdc++.h>
using namespace std;
map<int,map<int,int> >a;

这里开了一个map,a的第一个下标是一个int类型的key（代表柜子位置），第二个下标是里面map的key（柜子上的格子号），里面map的value就是储存的值

含义类似于两个地址叠加，合起来指向存储的东西

因为是两个地址，所以就不会出现二维数组无用空间开太大的问题，问题就解决了

代码如下

int main()
{
    int n,q;
    int did,i,j,k;
    cin>>n>>q; 
    for(int t=0;t<q;t++)
    {
        cin>>did;
        if(did==1)
        {
            cin>>i>>j>>k;
            a[i][j]=k;
        }
        else if(did==2)
        {
            cin>>i>>j;
            cout<<a[i][j]<<endl;
        }
    }
   return 0;
}

2.括号序列

 

 

 

 

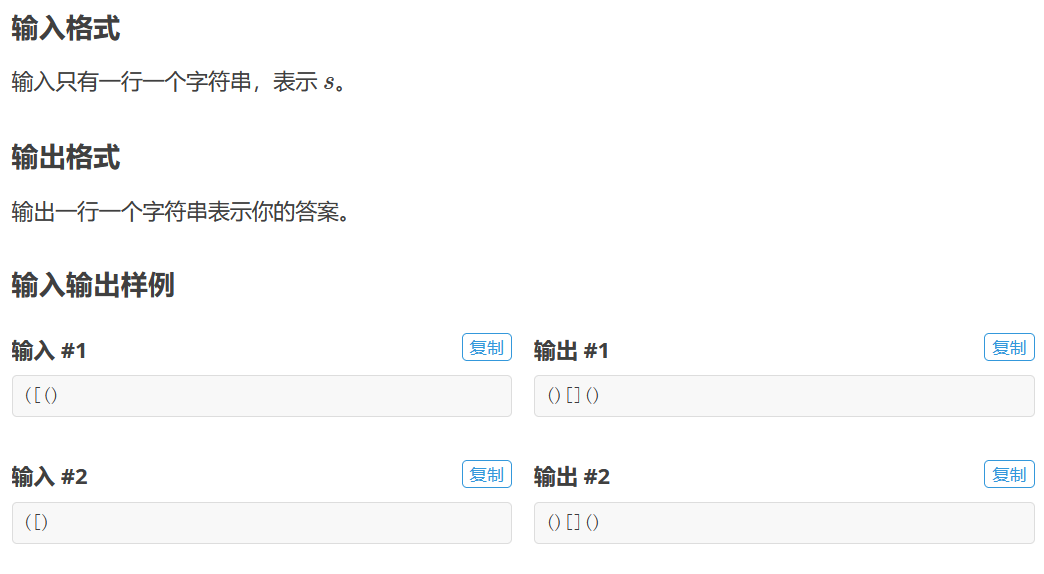
该题重在读懂题

注意以下几个要点

1.要依据右括号来判断是否成对

2.若出现([)或[)]这种夹不同括号的情况则要全部自成对（除非里面不同括号已经成对了）

因此从左到右依据右括号判断，还可规避在判断外部括号时，内部括号还不知道有没有成对的问题

#include<bits/stdc++.h>
using namespace std;
int b[10000]={0};
int main(void)
{
    char a[10000];
    cin>>a;
    int l=strlen(a);
    for(int i=0;i<l;i++)
    {
//从右括号判断是否成对，是则在b数组中对应变成1
        if(a[i]==')')
        {
            for(int j=i-1;j>=0;j--)
            {
                if(a[j]=='['&&b[j]==0)break;
                else if(a[j]=='('&&b[j]!=1)
                {
                    b[i]=1;
                    b[j]=1;
                    break;
                }
            }
        }
        else if(a[i]==']')
        {
            for(int j=i-1;j>=0;j--)
            {
                if(a[j]=='('&&b[j]==0)break;
                if(a[j]=='['&&b[j]!=1)
                {
                    b[i]=1;
                    b[j]=1;
                    break;
                }
            }
        }
    }
//输出
    for(int i=0;i<l;i++)
    {
        if(b[i]==1)cout<<a[i];
        else
        {
            if(a[i]=='(')cout<<"()";
            else if(a[i]=='[')cout<<"[]";
            else if(a[i]==']')cout<<"[]";
            else cout<<"()";
        }
    }
    return 0;
}

3.后缀表达式

 

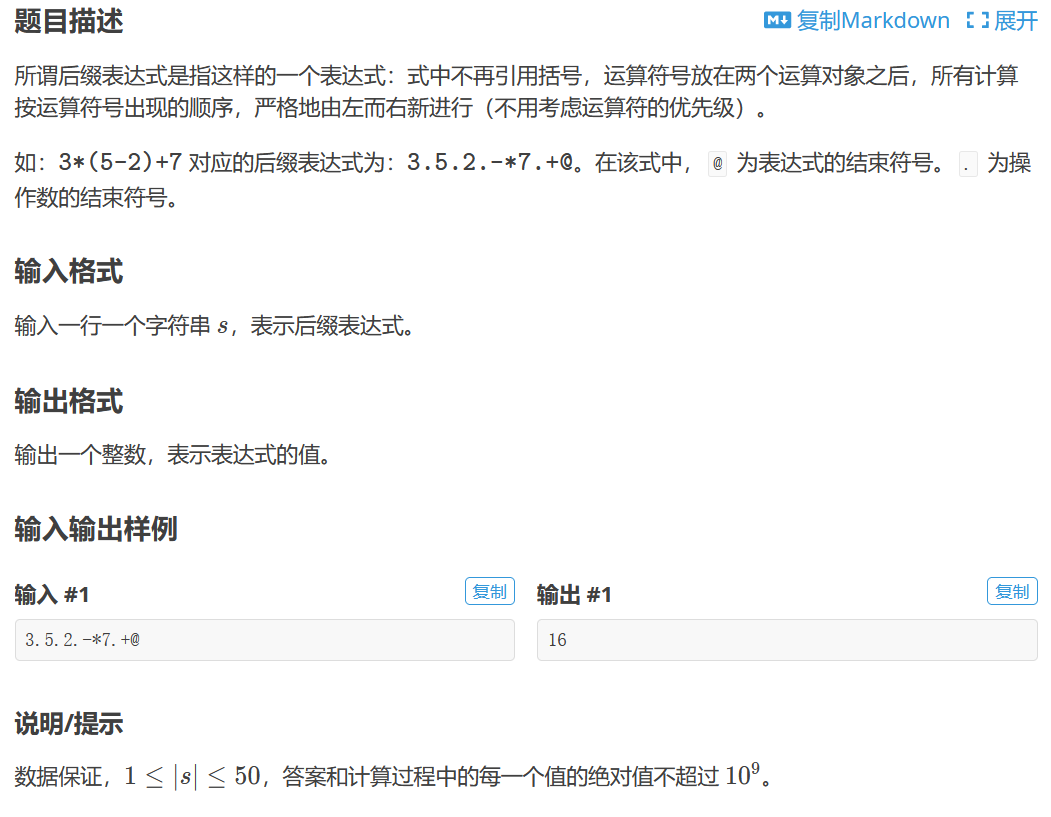
以堆栈的方式将数字储存进数组里

#include<bits/stdc++.h>
using namespace std;
int a[1005];//a的作用类似于栈
int main()
{
    char c;
//now存数，i记a中数字个数
    int i=0,now=0;
    while(cin>>c&&c!='@'){
        if(c>=48&&c<=57)
        {
            now*=10;
            now+=c-48;
        }
//存数，以类似堆栈的方式存到a数组里
        else if(c=='.')
        {
            i++;
            a[i]=now;
            now=0;
        }

如果碰到运算符则把最上面两数进行相应的运算

然后把值存到前一个数的位置上

        else if(c=='+')//计算 
        {
            a[i-1]=a[i-1]+a[i];
            a[i]=0;
            i--;
        } 
        else if(c=='-')
        {
            a[i-1]=a[i-1]-a[i];
            a[i]=0;
            i--;
        } 
        else if(c=='*')
        {
            a[i-1]=a[i-1]*a[i];
            a[i]=0;
            i--;
        } 
        else if(c=='/')
        {
            a[i-1]=a[i-1]/a[i];
            a[i]=0;
            i--;
        } 
    }

最终留在a[1]上的就是结果

4.队列安排

 

该题若直接用数组，那么每有一个人插入，那么其插入位置后的所有人都要往后移一位，数据可能会爆

但通过观察发现，插入一个人时，除了其插入的位置，其他人的相对位置是不变的

那么就可以抽象为一个路径问题，比如原路径为a->b->d->c，在a右侧插入一个e

则路径变为a->e->b->d->c，b、d、c的顺序没变

删除掉e则变回原路径

因此用增减路径点的思路来做这个题

 

#include<bits/stdc++.h>
using namespace std;
struct w
{
    int l,r;
} ab[100005];
int main(void)
{
    int n,p,k,m;
    cin>>n;
//初始化0，1的路径，这里固定了最后一位的右边一定是0
    ab[0].l=0;
    ab[0].r=1;
    ab[1].r=0;
    ab[1].l=0;
    for(int i=2;i<=n;i++)
    {
        cin>>k>>p;
//在k的p侧增加一个i路径点
        if(p==0) 
        {
            ab[i].r=k;
            ab[i].l=ab[k].l;
            ab[k].l=i;
            ab[ab[i].l].r=i;
        }
        else
        {
            ab[i].r=ab[k].r;
            ab[i].l=k;
            ab[k].r=i;
            ab[ab[i].r].l=i;
        }
    }
//删去m个路径点
    cin>>m;
    for(int i=0;i<m;i++)
    {
        int a;
        cin>>a;
        if(ab[a].l==0&&ab[a].r==0)continue;
        else
        {
            ab[ab[a].r].l=ab[a].l;
            ab[ab[a].l].r=ab[a].r;
            ab[a].l=0;
            ab[a].r=0;
        }
    }
    for (int i=ab[0].r;i!=0;i=ab[i].r)cout<<i<<' ';
    return 0;
}