bzoj 1492
这道题真好。。。
首先,感觉像DP,但是如果按照原题意,有无数个状态,每个状态又有无数个转移。
然后思考,我们每次买一部分和卖一部分的原因是什么,如果没有那个比例(就是rate=1恒成立),那么很容易贪心证明每次必须买完或卖完,但加了比例后就没那么好证明了,感觉一下吧。
然后就可以写DP方程了(dp[i]表示通过前i天的交易,到达第i天时,身上最多的钱)
(内层的max前面那项很好解决主要是后面的那个转移,所以后面就之考虑后面那个)
这个转移中有i的信息与j的信息相乘的项,所以考虑是否可用斜率优化,设有两项:k<j<i,那么“选j比选k优”当且仅当:
我们化简:
设:
那么就是:
走到这我们就走不动了,因为f或g函数没有单调性,我们就没办法像普通的斜率优化那样除过去。这时我们回过头,发现我们设的k<j<i没有什么用,对上面那个式子的化简没有什么用,想想后,恍然大悟,我们以前斜率优化的时候,之所以设k<j<i是因为上面的f函数或g函数是单调的,我们设了k<j<i的目的主要是为了让g[j]-g[k]或f[j]-f[k]的正负恒定,这样就可以除过去了,这道题,我们不妨不设k<j<i,而直接设j<i,k<i,且g[j]>g[k](当然也可以设g[j]<g[k],f[i]>f[k]或f[i]<f[k]),这样上面那个式子就可以化简了:
是不是很像斜率优化,和斜率优化一样,我们把每个决策点j看成是一个点:(g[j],f[j]),容易证明,最优决策点一定是上凸壳上的一个点:
以上图为例子,当前计算的状态是i(其对应斜率-b[i]/a[i]为绿线的斜率),后很多决策点(红点),上凸壳上的点已经标号。此时最有决策点是B,最优决策点的左右两条直线的斜率把当前状态的斜率卡在中间。
这道题和普通的斜率优化不同的地方在于,普通的斜率优化的状态的斜率是单调的(即绿线的斜率),并且每个状态作为决策点的横坐标也是单调的(即每次新加入的蓝点的横坐标是单调的),这就让我们可以均摊O(1)地插入一个点到凸包并且O(1)地找到我们的最优决策点。
但这道题就不行,上面两个性质它都不满足,所以一般的思路是用平衡树维护一个上凸壳,这样插入一个决策点和找一个最有决策点的复杂度都是O(logn)的,可以搞定这道题,但我没写过动态维护凸壳,听说难写难调。
然后这道题就成了时间分治(cdq分治?)的例题。
时间分治是这样的:对于一个序列:
ABABAABBBABABABABABABAAB
其中B是一个询问,其答案取决于其前面的A,并且A对B的影响独立(即可以用单个A就可以更新B,只要前面的A都更新过B,那么B的答案就是正确的)。那么就可以时间分治了。对于上面那个序列,我们先拆成两半:
1、ABABAABBBABA
2、BABABABABAAB
我们解决了1、2两个子问题后,合并时只要把1中的A对2中的B的影响更新到B,那么就可以了。
ABABAABBBABA BABABABABAAB
即只要用红色的A去更新蓝色的B,那么当前的任务就完成了,将有颜色的部分提出来,我们发现A全在B前面,就是说我们只需解决“先给出所有A,再给出所有B”这个问题就可以了。(这个就提供给我们了一个将ABABAB问题并且满足上面那个影响独立性质的问题以一个log的复杂度变成AAABBB问题)
至于这道题,我们的A是给出一个点,我们的B是前面的所有点选一个最优决策点来更新B,因为只要我们把可能最优的A去更新B,那么B就一定会得到最优答案,所以满足“影响独立”原则,这道题有个细节要注意,就是我们的A和B是合在一起的,并且只有知道了B的答案,才知道A,也就是说我们每次分治时,要先解决左边的子问题,然后用左边的决策点去更新右边的询问点,在解决右边的子问题。
感谢xhr和cdq的论文。

1 /************************************************************** 2 Problem: 1492 3 User: idy002 4 Language: C++ 5 Result: Accepted 6 Time:1564 ms 7 Memory:11508 kb 8 ****************************************************************/ 9 10 /* 11 dp[1] = s 12 dp[i] = max{ dp[i], dp[j]*(a[i]*r[j]+b[i])/(a[j]*r[j]+b[j]) | j in [1,i) } i in [2,n] 13 14 f[i] = (dp[i]*r[i])/(a[i]*r[i]+b[i]) 15 g[i] = dp[i]/(a[i]*r[i]+b[i]) 16 dp[i] = max{ dp[i], f[j]*a[i]+g[j]*b[i] | j in [1,i) } i in [2,n] 17 ( g[i], f[i] ) as point 18 k[i] = -b[i]/a[i] 19 */ 20 #include <cstdio> 21 #include <cmath> 22 #include <iostream> 23 #include <vector> 24 #include <algorithm> 25 #define N 100010 26 #define eps 1e-10 27 #define fprintf(...) 28 using namespace std; 29 30 int sg( double x ) { return (x>-eps)-(x<eps); } 31 struct Vector { 32 double x, y; 33 Vector(){} 34 Vector( double x, double y ):x(x),y(y){} 35 Vector operator+( const Vector &b ) const { return Vector(x+b.x,y+b.y); } 36 Vector operator-( const Vector &b ) const { return Vector(x-b.x,y-b.y); } 37 Vector operator*( double b ) const { return Vector(x*b,y*b); } 38 Vector operator/( double b ) const { return Vector(x/b,y/b); } 39 double operator^( const Vector &b ) const { return x*b.y-y*b.x; } 40 double operator&( const Vector &b ) const { return x*b.x+y*b.y; } 41 double ang() { return atan2(y,x); } 42 bool operator<( const Vector &b ) const { return x<b.x||(x==b.x&&y<b.y); } 43 }; 44 typedef Vector Point; 45 46 int n; 47 double s; 48 double aa[N], bb[N], rr[N], kk[N]; 49 double f[N], g[N], dp[N]; 50 double ag[N]; 51 52 bool onleft( Point &a, Point &b, Point &c ) { 53 return sg( (b-a)^(c-a) ) > 0; 54 } 55 void convex( vector<Point> &p, vector<Point> &c ) { // up convex 56 sort( p.begin(), p.end() ); 57 c.push_back( p.back() ); 58 for( int i=p.size()-2; i>=0; i-- ) { 59 while( c.size()>1 && !onleft( c[c.size()-2], c[c.size()-1], p[i] ) ) 60 c.pop_back(); 61 c.push_back( p[i] ); 62 } 63 } 64 bool cmp_k( int a, int b ) { 65 return kk[a]>kk[b]; 66 } 67 void cdq( int lf, int rg, vector<Point> &c ) { 68 if( lf==rg ) { 69 int i=lf; 70 dp[i] = max( dp[i], s ); 71 s = max( dp[i], s ); 72 g[i] = dp[i]/(aa[i]*rr[i]+bb[i]); 73 f[i] = rr[i]*g[i]; 74 c.push_back( Point(g[i],f[i]) ); 75 // fprintf( stderr, "dp[%d] = %lf (%.2lf,%.2lf) %.2lf\n", i, dp[i], g[i], f[i], kk[i] ); 76 // fprintf( stderr, "i=%d dp=%.2lf f=%.2lf g=%.2lf\n", 77 // i, dp[i], f[i], g[i] ); 78 return; 79 } 80 int mid=(lf+rg)>>1; 81 vector<Point> cl, cr; 82 vector<int> vr; 83 cdq( lf, mid, cl ); 84 for( int i=0; i<cl.size()-1; i++ ) { 85 Vector u = cl[i+1]-cl[i]; 86 if( sg(u.x)==0 ) { 87 if( u.y>0.0 ) 88 ag[i] = 1e20; 89 else 90 ag[i] = -1e20; 91 } else 92 ag[i] = u.y/u.x; 93 } 94 for( int i=mid+1; i<=rg; i++ ) 95 vr.push_back( i ); 96 sort( vr.begin(), vr.end(), cmp_k ); 97 for( int i=0,j=0; j<vr.size(); j++ ) { 98 int k=vr[j]; 99 while( i<cl.size()-1 && ag[i]>kk[k] ) i++; 100 dp[k] = max( dp[k], cl[i].x*bb[k]+cl[i].y*aa[k] ); 101 } 102 cdq( mid+1, rg, cr ); 103 for( int i=0; i<cr.size(); i++ ) 104 cl.push_back( cr[i] ); 105 convex( cl, c ); 106 reverse( c.begin(), c.end() ); 107 } 108 int main() { 109 scanf( "%d%lf", &n, &s ); 110 for( int i=1; i<=n; i++ ) { 111 scanf( "%lf%lf%lf", aa+i, bb+i, rr+i ); 112 kk[i] = -bb[i]/aa[i]; 113 } 114 vector<Point> c; 115 cdq(1,n,c); 116 double ans = 0.0; 117 for( int i=1; i<=n; i++ ) 118 ans = max( ans, dp[i] ); 119 printf( "%.3lf\n", ans ); 120 } 121 122

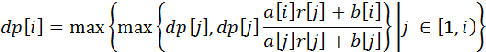

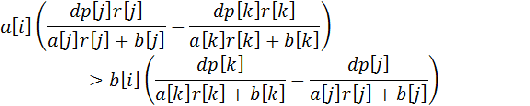
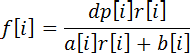
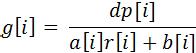
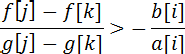



 浙公网安备 33010602011771号
浙公网安备 33010602011771号