最长回文子串

介绍中心扩展算法、动态规划、马拉车算法在具体求解最长回文子串中的使用。

一、题目

  给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

解法一：使用暴力解法，就是对于给定字符串获取其每一个子串。然后判断该子串是否为回文串，如果是，则和以求得的最长回文子串比较长度，判断是否需要更新最长回文子串。最后所有子串遍历完则可得到结果。时间复杂度为O(n³)。

解法二：使用中心扩展算法，遍历一次字符串中每个字符。对于每个字符，都要以该字符为中心向两边扩展，直至两边最外字符不相等，则求得以该字符为中心的最长回文子串。另外若该字符与其上一个字符相等，则需求出以这两个字符为中心的最长回文子串。之后取两者中最长的和目前已知最长回文子串比较长度，判断是否需要更新最长回文子串。算法时间复杂度为O(n²)。

public static String longestPalindrome(String s) {
    String LPString = "";
    String currString = "";
    char[] chars = s.toCharArray();
    for (int i = 0; i < s.length(); i ++) {
        int l = i - 1;
        int r = i + 1;
        if (i > 0 && chars[i] == chars[i - 1]) {
            currString = getPalindrome(s, chars, l - 1, r);
        }
        String tempString = getPalindrome(s, chars, l, r);
        currString = currString.length() > tempString.length() ? currString : tempString;
        if (currString.length() > LPString.length()) {
            LPString = currString;
        }
    }
    return LPString;
}
public static String getPalindrome(String s, char[] chars, int l, int r) {
    while (l >= 0 && r < s.length()) {
        if (chars[l] != chars[r]) {
            break;
        }
        l --;
        r ++;
    }
return s.substring(l + 1, r);
}

解法三：动态规划法是在暴力法的基础上进行优化，每次判断字符串[i，j]是否为回文串，利用空间存储已经判断的[i + 1，j - 1]是否为回文串，此时只需判断第i个字符和第j个字符是否相当即可。且若满足，则其回文串长度就是i - j + 1。时间复杂度为O(n²)。

解法四：马拉车算法(Manacher's Algortithm)，首先字符串中每个字符的两边都要有一个填充字符，所以填充后字符串长度为2 * n + 1。那么此时只需判断以每个字符为中心的扩展回文串，中心扩展法中以双字符为中心的扩展方法就转为了以填充字符为中心。另外可以发现扩展后字符回文串半径为原字符的回文串长度。

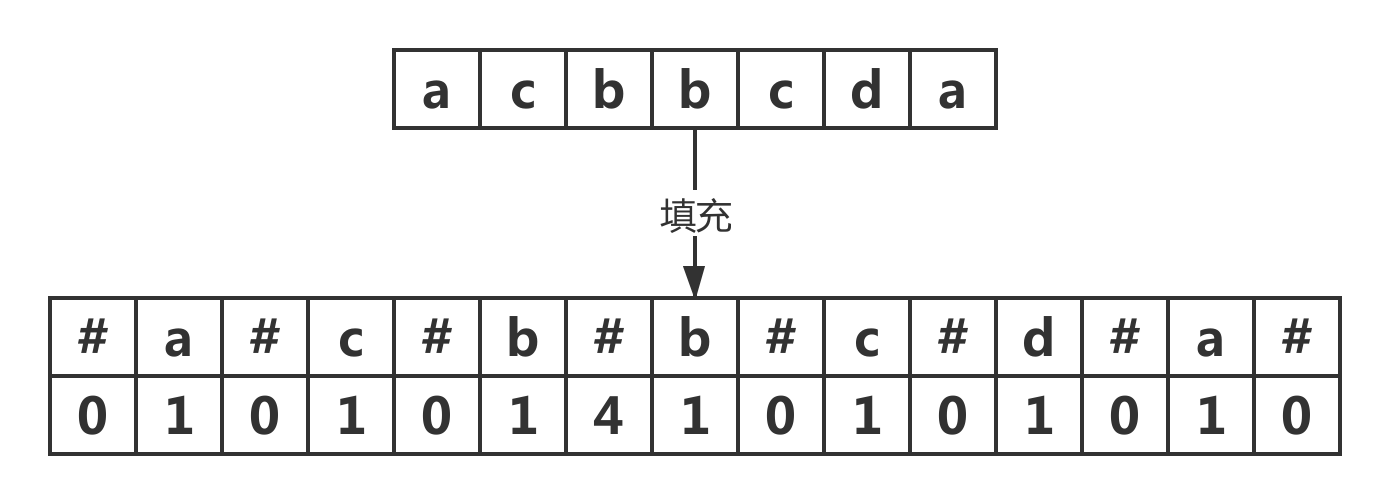
  这里可以发现如果我们要求的字符x处在上一个字符y的回文串里，那么假设x^，是x关于y对称的字符。如果x^，的回文串落在y中，利用y回文串对称性，那么x的回文串长度就是x^，的回文串长度。而若x^，回文串处在y的边缘或外部，那么x回文串长度至少大于等于x当前下标到y的边缘长度，而之后则是利用中心扩展的方法继续判断。

  所以引入一个对称中心和其半径，我们只要保证其中心加半径长越大。每次遍历求新字符的回文串，该字符会大概率落在该对称中心回文串内，在结合上一步的对称性，就能保证每次如果扩展，那么都是扩展对称中心回文串外的字符，所以整个字符串遍历下来，减少重复扩展字符。最后只需要记录下回文串半径最大的那个回文串的中心与半径，就可以获得最长回文子串。时间复杂度为O(n)

public static String longestPalindrome(String s) {
    int maxLength = 0;
    int index = 0;
    char[] chars = expandString(s);
    int[] P = new int[chars.length];
    int C = 0;
    int R = 0;
    for (int i = 1; i < chars.length - 1; i ++) {
        int iMarror = 2 * C - i;
        if (R > i) {
            P[i] = Math.min(R - i, P[iMarror]);
        }
        while (i - P[i] - 1 >= 0 && i + P[i] + 1 < chars.length ) {
            if (chars[i - P[i] - 1] != chars[i + P[i] + 1]) {
                break;
            }
            P[i] ++;
        }
        if (i + P[i] > R) {
            R = i + P[i];
            C = i;
        }
        if (P[i] > maxLength) {
            maxLength = P[i];
            index = i;
        }
    }
    int start = (index - maxLength) / 2;
    int end = start + maxLength;
    return s.substring(start, end);
}
public static char[] expandString(String s) {
    char[] chars = s.toCharArray();
    char[] chars1 = new char[s.length() * 2 + 1];
    for (int i = 0; i < s.length(); i ++) {
        chars1[2 * i] = '#';
        chars1[2 * i + 1] = chars[i];
    }
    chars1[2 * s.length()] = '#';
    return chars1;
}