94.二叉树的中序遍历

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

示例 1：

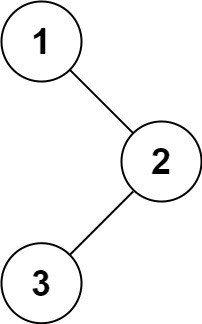
输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

• 树中节点数目在范围 [0, 100] 内
• -100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

思路：中序遍历：左节点->根节点->右节点

方法一：递归

时间复杂度：O(n)，其中 n为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次。

空间复杂度：O(n)，空间复杂度取决于递归的栈深度，而栈深度在二叉树为一条链的情况下会达到 O(n)的级别。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var inorderTraversal = function (root) {
    const res = [];
    const inorder = (root) => {
        if (!root) {
            return;
        }
        inorder(root.left);
        res.push(root.val);
        inorder(root.right);
    }
    inorder(root);
    return res;
};

方法二：迭代

时间复杂度：O(n)，其中 n为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次

空间复杂度：O(n)，空间复杂度取决于栈深度，而栈深度在二叉树为一条链的情况下会达到 O(n)的级别

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var inorderTraversal = function(root) {
const res = [];
const stack = [];
while(root||stack.length){
    while(root){
        stack.push(root);
        root = root.left;
    }
    root = stack.pop();
    res.push(root.val);
    root = root.right;
    }
    return res;
};

 方法三：Morris遍历

时间复杂度：O(n)，其中n为二叉搜索树的节点个数。Morris遍历中每个节点会被访问两次，因此总时间复杂度为O(2n)=O(n)

空间复杂度：O(1)

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var inorderTraversal = function (root) {
    const res = [];
    let predecessor = null;
    while (root) {
        if (root.left) {
            predecessor = root.left;
            while (predecessor.right && predecessor.right !== root) {
                predecessor = predecessor.right;
            }
            if (!predecessor.right) {
                predecessor.right = root;
                root = root.left;
            } else {
                res.push(root.val);
                predecessor.right = null;
                root = root.right;
            }
        }
        else {
            res.push(root.val);
            root = root.right;
        }
    }
    return res;
};