算法模板——树链剖分
说明一下,本文是从我另一个博客直接搬过来的,所以就放到原创里了,其实原文发布时间也是比这要早滴QwQ
时隔多年,再来更新一篇文章QwQ
简介
树链剖分是一种把树拆成链的技巧,主要目的是方便用各种数据结构来维护。下面的是线段树的模板。题目在此。前置技能
线段树,有自己用的习惯的存图方法。用处
- 在树上进行区间操作
- 常见操作参考题目。
- 两个节点
x和y最短路径上所有节点的值都加上某个数z - 两个节点
x和y最短路径上所有节点的值求和 - 某个节点
x的子树上所有节点都加上z - 子树求和
- 两个节点
思路
把一棵树拆成若干条不相关的链,然后用线段树去维护。拆成链不就有区间了嘛,然后就可以上线段树啦。若干概念
- 重儿子:一个节点的所有子节点中,子树最大(就是整个子树的所有节点数最多)的子节点。
- 轻儿子:不是重儿子的子节点。
- 重边:连接两个重儿子的边。
- 重链:若干重边和重儿子连接起来形成的一条链。
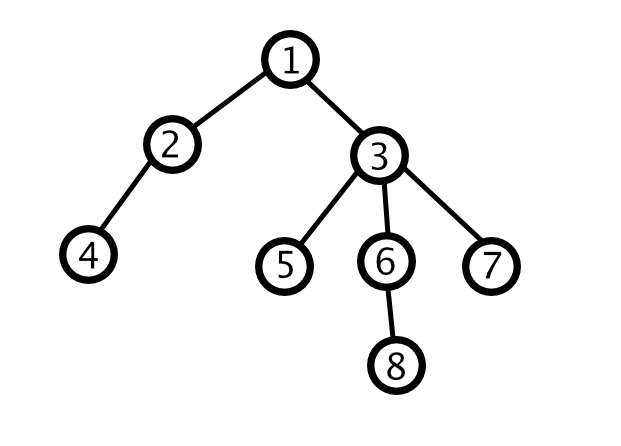
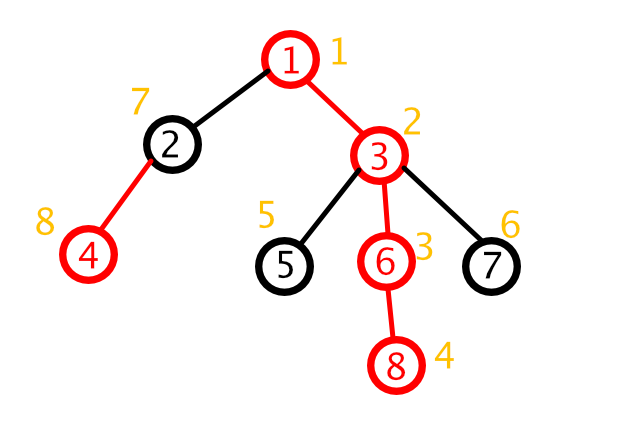
这是一棵树
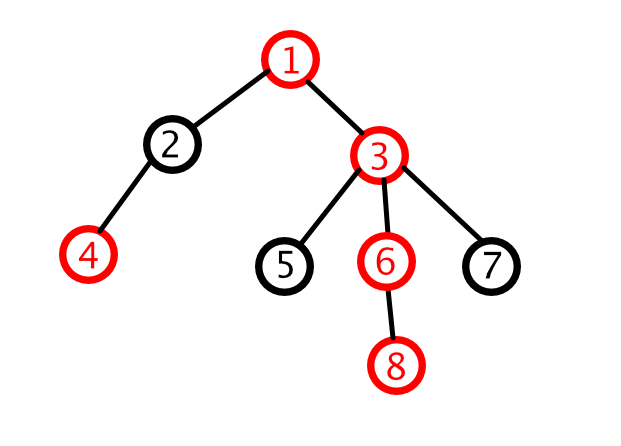
上图中,标红的点就是重儿子(根节点不是重儿子,标错了)。
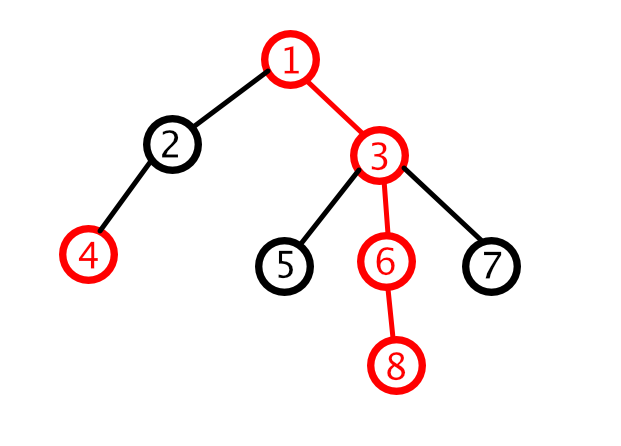
上图中,标红的边就是重边。而,1->3->6->8就是一条重链。
我们在考虑重链时,我们往往把树的根节点考虑到它的重链中。
继续讲思路
有了轻重链以后,我们就能维护树了,但是现在树上的编号是乱的。如果我们想在树上跑线段树,就需要对树上的节点进行重新编号。重新编号
我们采用dfs的方式进行重新编号。- 对于每棵子树,优先给重儿子编号。
因为这样可以保证一条链上的编号都是连续的。
上图,顺便贴一下代码:
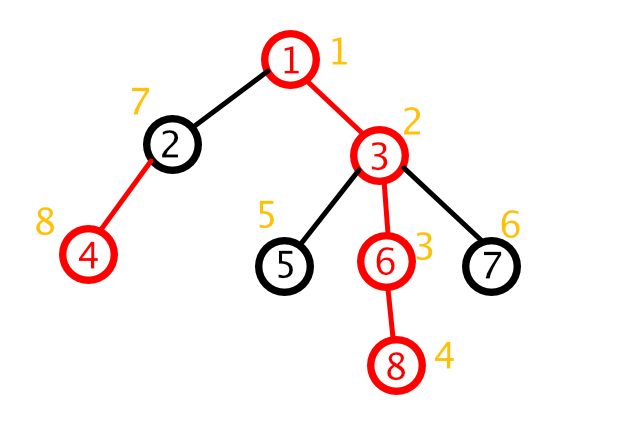
黄色的就是新的编号,而红色的边连起来的,就是一条一条的链。
int cnt = 0; // 用于重新编号的计数
void dfs2(int nd, int topf) { //nd:当前节点 topf:这条链的顶端
idx[nd] = ++cnt; //idx[原编号]=新编号
b[cnt] = a[nd]; //b[新编号]=a[原编号],存储节点的值
top[nd] = topf; //top[原编号]:点所在链的顶端节点的原编号
if (!son[nd]) return ; //son[原编号]:该节点的重儿子的原编号
dfs2(son[nd], topf); //优先处理重儿子
for (int i = head[nd]; i != -1; i = edge[i].nxt) { //枚举所有子节点
int j = edge[i].to;
if (j == fa[nd] || j == son[nd]) continue;
dfs2(j, j); //对于每个轻儿子,显然这个轻儿子本身就是它所在链的顶端节点,否则在上面的dfs2(son[nd], topf);过程中就处理过了。
}
}
结合代码理解一下,上图中存在的链有这么几条(下面是原编号):
- 1->3->6->8
- 2->4
- 5
- 7
一些特点
- 每条链的新编号都是连续的
- 每棵子树的新编号也都是连续的
开始写代码
各标识符的含义://原编号
int a[maxn]; //节点的值
int idx[maxn]; //节点对应的新编号
int top[maxn]; //节点所在链的顶端的原编号
int fa[maxn]; //节点的父亲的原编号
int son[maxn]; //节点的重儿子的原编号
int siz_tree[maxn]; //该节点为根的子树的大小
int depth[maxn]; //节点的深度
int root; //根节点的编号(参考题目)
int MOD; //结果对MOD取模(参考题目)
//新编号
int b[maxn]; //节点的值
int SegTree[maxn << 2]; //用来存储线段树
int lazy[maxn << 2]; //线段树的lazy tag
//存图
struct Edge {
int to, nxt;
}edge[maxn << 1];
int num_edge, head[maxn];
前置工作
上面的dfs2函数将树拆分成了链,但是在dfs2之前,我们还有一些东西需要处理:
- 找到每个节点的重儿子
- 找到每个节点的父亲
- 标记每个节点的子树大小
- 标记每个节点的深度。深度在执行链上加法和链上求和用的。
void dfs1(int nd, int f, int deep) { //nd:当前操作的节点 f:当前节点的父节点 deep:当前节点的深度
fa[nd] = f;
depth[nd] = deep; //depth[原编号]=该节点的深度
siz_tree[nd] = 1; //siz_tree[原编号]=该节点的子树大小,这里初始化成1(自己的大小为1)
int max_son = -1; //目前最大子树的大小
for (int i = head[nd]; i != -1; i = edge[i].nxt) { //枚举每个子节点
int j = edge[i].to;
if (j == fa[nd]) continue;
dfs1(j, nd, deep + 1); //处理子节点j
siz_tree[nd] += siz_tree[j]; //更新树的大小
if (siz_tree[j] > max_son) { //更新重儿子
max_son = siz_tree[j];
son[nd] = j;
}
}
}
拆分成链
和上面的dfs2代码完全一样:
int cnt = 0; // 用于重新编号的计数
void dfs2(int nd, int topf) { //nd:当前节点 topf:这条链的顶端
idx[nd] = ++cnt; //idx[原编号]=新编号
b[cnt] = a[nd]; //b[新编号]=a[原编号],存储节点的值
top[nd] = topf; //top[原编号]:点所在链的顶端节点的原编号
if (!son[nd]) return ; //son[原编号]:该节点的重儿子的原编号
dfs2(son[nd], topf); //优先处理重儿子
for (int i = head[nd]; i != -1; i = edge[i].nxt) { //枚举所有子节点
int j = edge[i].to;
if (j == fa[nd] || j == son[nd]) continue;
dfs2(j, j); //对于每个轻儿子,显然这个轻儿子本身就是它所在链的顶端节点,否则在上面的dfs2(son[nd], topf);过程中就处理过了。
}
}
构造线段树
注意:线段树里访问和操作节点时,都是访问的新编号。将数据结构和构造链分开,方便复用,也方便我们构造数据结构。下面完全就是个线段树的模版。每个人有自己的写法,这里贴一下我的写法:
void PushUp(int nd) {
SegTree[nd] = (SegTree[nd << 1] + SegTree[nd << 1 | 1]) % MOD;
}
void Build(int nd, int l, int r) {
if (l == r) {
SegTree[nd] = b[l];
return ;
}
int mid = (l + r) >> 1;
Build(nd << 1, l, mid);
Build(nd << 1 | 1, mid + 1, r);
PushUp(nd);
}
void PushDown(int nd, int ln, int rn) {
if (lazy[nd]) {
lazy[nd << 1] += lazy[nd];
lazy[nd << 1 | 1] += lazy[nd];
SegTree[nd << 1] = (SegTree[nd << 1] + ln * lazy[nd]) % MOD;
SegTree[nd << 1 | 1] = (SegTree[nd << 1 | 1] + rn * lazy[nd]) % MOD;
lazy[nd] = 0;
}
}
void Update(int nd, int l, int r, int L, int R, int val) {
if (L <= l && r <= R) {
SegTree[nd] = (SegTree[nd] + (r - l + 1) * val) % MOD;
lazy[nd] += val;
return ;
}
int mid = (l + r) >> 1;
PushDown(nd, mid - l + 1, r - mid);
if (L <= mid) Update(nd << 1, l, mid, L, R, val);
if (R > mid) Update(nd << 1 | 1, mid + 1, r, L, R, val);
PushUp(nd);
}
int Query(int nd, int l, int r, int L, int R) {
if (L <= l && r <= R) {
return SegTree[nd] % MOD;
}
int mid = (l + r) >> 1;
PushDown(nd, mid - l + 1, r - mid);
int ans = 0;
if (L <= mid) ans = (ans + Query(nd << 1, l, mid, L, R)) % MOD;
if (R > mid) ans = (ans + Query(nd << 1 | 1, mid + 1, r, L, R)) % MOD;
return ans;
}
那个% MOD的含义请参考题目。
更新和查询
链更新
其实链更新有点麻烦。先考虑当两个点不在同一条链上时,说明它们的top[x]不相同,这时就可以把x到top[x]之间的点都更新一遍(因为从L到R之间一定是通过它们的共同的根的)。
两个点在同一条链上时,直接Update(1, 1, N, idx[L], idx[R], val)就好了(同一条链上新编号相邻)
感性理解一波QwQ。
void line_Add(int L, int R, int val) { //这里的L和R指的是两个节点的原编号,并不一定要L小R大,val是要加上的值
val %= MOD;
while (top[L] != top[R]) { //两者不在同一条链上
if (depth[top[L]] < depth[top[R]]) swap(L, R); //优先处理顶端深度较大的
Update(1, 1, N, idx[top[L]], idx[L], val); //更新L到L的顶端这一部分。这一部分的新编号是连续的,所以可以直接这样处理。注意顶端的节点新编号比下面的编号一定要小。
L = fa[top[L]]; //注意这里是更新到top[L]的父节点
}
if (depth[L] > depth[R]) swap(L, R);
Update(1, 1, N, idx[L], idx[R], val); //二者在同一条链上
}
下面结合图模拟一下:
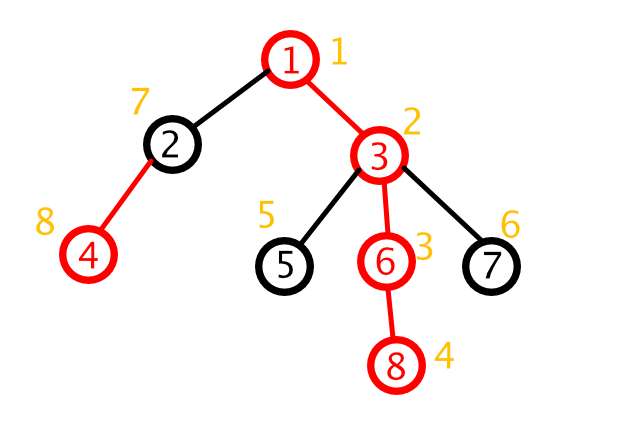
比如说,我们要在4~7之间的节点都加上1。现在它们不在同一条链上(假设我们执行line_Add(4, 7, 1)),那么我们先处理4所在的链:
- 比较4和7的深度,
depth[4] < depth[7]不成立,不交换L和R - 更新4所在的链:4~2这条链
Update(1, 1, N, idx[top[4]], idx[4], 1)- 也就是
Update(1, 1, N, 7, 8, 1) L = fa[top[4]]也就是L = fa[2]也就是L = 1
- 1和7不在同一条链上
- 比较1和7的深度。
depth[1] < depth[7]成立,交换L和R - 重复上述步骤
- ……
L = fa[7] = 3,R = 1(因为比较1和7的顶端深度时交换过L和R)
- 1和3在同一条链上
- 跳出
while - 比较
L(3)和R(1)的深度 - 交换
L和R Update(1, 1, N, idx[1], idx[3], 1);
这样,节点4、2、1、3、7就都被更新过了。
链查询
和链更新一样,只不过把更新换成了查询(我都不想写注释了,因为它们实在是太像了QwQ):int line_Query(int L, int R) {
int ans = 0;
while (top[L] != top[R]) {
if (depth[top[L]] < depth[top[R]]) swap(L, R);
ans += Query(1, 1, N, idx[top[L]], idx[L]);
ans %= MOD;
L = fa[top[L]];
}
if (depth[L] > depth[R]) swap(L, R);
ans += Query(1, 1, N, idx[L], idx[R]);
ans %= MOD;
return ans;
}
树更新
树更新比较好理解:对于一棵子树x,它的编号范围就是idx[x] ~ idx[x] + siz_tree[x] - 1。
比如以3(原节点)为根的子树:
idx[3] = 2siz_tree[3] = 5idx[3] + siz_tree[3] - 1 == 6
所以树更新如下:
void tree_Add(int nd, int val) {
Update(1, 1, N, idx[nd], idx[nd] + siz_tree[nd] - 1, val);
}
树查询
同上int tree_Query(int nd) {
return Query(1, 1, N, idx[nd], idx[nd] + siz_tree[nd] - 1) % MOD;
}
完整代码
luogu P3384#include <cstdio>
#include <cstring>
#include <algorithm>
using std::max;
using std::min;
using std::swap;
const int maxn = 100005;
int a[maxn], b[maxn], idx[maxn], top[maxn], fa[maxn], son[maxn], SegTree[maxn << 2], lazy[maxn << 2], siz_tree[maxn], depth[maxn];
int N, M;
struct Edge {
int to, nxt;
}edge[maxn << 1];
int num_edge, head[maxn], root, MOD;
void AddEdge(int from, int to) {
edge[num_edge].to = to;
edge[num_edge].nxt = head[from];
head[from] = num_edge;
num_edge++;
}
void dfs1(int nd, int f, int deep) {
fa[nd] = f;
depth[nd] = deep;
siz_tree[nd] = 1;
int max_son = -1;
for (int i = head[nd]; i != -1; i = edge[i].nxt) {
int j = edge[i].to;
if (j == fa[nd]) continue;
dfs1(j, nd, deep + 1);
siz_tree[nd] += siz_tree[j];
if (siz_tree[j] > max_son) {
max_son = siz_tree[j];
son[nd] = j;
}
}
}
int cnt = 0;
void dfs2(int nd, int topf) {
idx[nd] = ++cnt;
b[cnt] = a[nd];
top[nd] = topf;
if (!son[nd]) return ;
dfs2(son[nd], topf);
for (int i = head[nd]; i != -1; i = edge[i].nxt) {
int j = edge[i].to;
if (j == fa[nd] || j == son[nd]) continue;
dfs2(j, j);
}
}
void PushUp(int nd) {
SegTree[nd] = (SegTree[nd << 1] + SegTree[nd << 1 | 1]) % MOD;
}
void Build(int nd, int l, int r) {
if (l == r) {
SegTree[nd] = b[l];
return ;
}
int mid = (l + r) >> 1;
Build(nd << 1, l, mid);
Build(nd << 1 | 1, mid + 1, r);
PushUp(nd);
}
void PushDown(int nd, int ln, int rn) {
if (lazy[nd]) {
lazy[nd << 1] += lazy[nd];
lazy[nd << 1 | 1] += lazy[nd];
SegTree[nd << 1] = (SegTree[nd << 1] + ln * lazy[nd]) % MOD;
SegTree[nd << 1 | 1] = (SegTree[nd << 1 | 1] + rn * lazy[nd]) % MOD;
lazy[nd] = 0;
}
}
void Update(int nd, int l, int r, int L, int R, int val) {
if (L <= l && r <= R) {
SegTree[nd] = (SegTree[nd] + (r - l + 1) * val) % MOD;
lazy[nd] += val;
return ;
}
int mid = (l + r) >> 1;
PushDown(nd, mid - l + 1, r - mid);
if (L <= mid) Update(nd << 1, l, mid, L, R, val);
if (R > mid) Update(nd << 1 | 1, mid + 1, r, L, R, val);
PushUp(nd);
}
int Query(int nd, int l, int r, int L, int R) {
if (L <= l && r <= R) {
return SegTree[nd] % MOD;
}
int mid = (l + r) >> 1;
PushDown(nd, mid - l + 1, r - mid);
int ans = 0;
if (L <= mid) ans = (ans + Query(nd << 1, l, mid, L, R)) % MOD;
if (R > mid) ans = (ans + Query(nd << 1 | 1, mid + 1, r, L, R)) % MOD;
return ans;
}
void line_Add(int L, int R, int val) {
val %= MOD;
while (top[L] != top[R]) {
if (depth[top[L]] < depth[top[R]]) swap(L, R);
Update(1, 1, N, idx[top[L]], idx[L], val);
L = fa[top[L]];
}
if (depth[L] > depth[R]) swap(L, R);
Update(1, 1, N, idx[L], idx[R], val);
}
int line_Query(int L, int R) {
int ans = 0;
while (top[L] != top[R]) {
if (depth[top[L]] < depth[top[R]]) swap(L, R);
ans += Query(1, 1, N, idx[top[L]], idx[L]);
ans %= MOD;
L = fa[top[L]];
}
if (depth[L] > depth[R]) swap(L, R);
ans += Query(1, 1, N, idx[L], idx[R]);
ans %= MOD;
return ans;
}
void tree_Add(int nd, int val) {
Update(1, 1, N, idx[nd], idx[nd] + siz_tree[nd] - 1, val);
}
int tree_Query(int nd) {
return Query(1, 1, N, idx[nd], idx[nd] + siz_tree[nd] - 1) % MOD;
}
int read() {
int x = 0, f = 1;
char ch = getchar();
while (ch > '9' || ch < '0') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - '0';
ch = getchar();
}
return (x * f);
}
int main() {
memset(head, -1, sizeof(head));
N = read(); M = read(); root = read(); MOD = read();
for (int i = 1; i <= N; i++) a[i] = read();
for (int i = 1; i < N; i++) {
int x = read(), y = read();
AddEdge(x, y);
AddEdge(y, x);
}
dfs1(root, 0, 1);
dfs2(root, root);
Build(1, 1, N);
while (M--) {
int x, y, z, w;
x = read();
switch (x) {
case 1:
y = read(); z = read(); w = read();
line_Add(y, z, w);
break;
case 2:
y = read(); z = read();
printf("%d\n", line_Query(y, z));
break;
case 3:
y = read(); z = read();
tree_Add(y, z);
break;
case 4:
y = read();
printf("%d\n", tree_Query(y));
break;
default:
break;
}
}
}
本文迁移自作者原博客:icysky's Blog
原文作者: icysky
原文链接: 算法模板——树链剖分
版权声明: 本博客所有文章除特别声明外,均采用CC-BY-NC-SA 4.0许可协议。icysky's Blog 版权所有,转载请注明出处。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号