IEEE754浮点数

前言

　　Go语言之父Rob Pike大神曾吐槽：不能掌握正则表达式或浮点数就不配当码农！

　　You should not be permitted to write production code if you do not have an journeyman license in regular expressions or floating point math.

　　此前使用Java写Spark SQL业务时，也有遇到浮点数比较问题即x>70的记录行居然出现了70的记录，尽管SQL做了类型转换再比较也无济于事....

　　因此了解浮点数是很有必要的哟~~

什么是浮点数

　　电气和电子工程师协会IEEE对于计算机浮点数的存储、运算、表示等推出了IEEE754标准！

　　标准中规定：

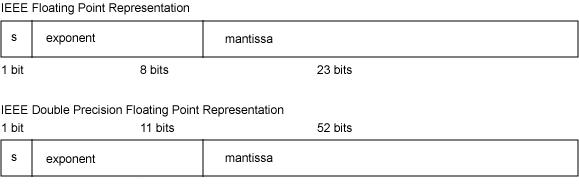
　　　　float32位单精度浮点数在机器中表示用 1 位表示数字的符号，用 8 位表示指数，用 23 位表示尾数。

　　　　double64位双精度浮点数，用 1 位表示符号，用 11 位表示指数，52 位表示尾数。

　　　　其中指数域也称为阶码。浮点数存储字节定义如图：

　　       

浮点数正规化

　　尾数不为0时，尾数域的最高有效位为1，这称为规格化。否则，以修改阶码同时左右移动小数点位置的办法，使其成为规格化数的形式。

　　浮点数x真值表示：

　　x=(−1)^S×(1.M)×2^e

　　float：　　　　e=E−127

　　double：　　   e=E−1023　

• S  符号位　　  0表示正 1表示负
• e  指数位  　　阶码E减去移码
• M 尾数位  　　二进制形式移码

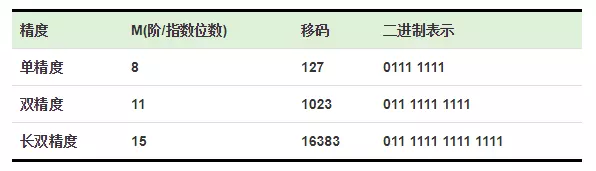
移码

　　移码是真值补码的符号位取反，一般用作浮点数的阶码，目的是便于浮点数运算时的对阶操作。

　　对于定点整数，计算机一般采用补码的来存储。

　　正整数的符号位为0，反码和补码等同于原码。

　　负整数符号位都为1，原码，反码和补码的表示都不相同，由负数原码表示法变成反码和补码有如下规则：
　　（1）原码符号位为1不变，整数的每一位二进制数位求反得反码；
　　（2）反码符号位为1不变，反码数值位最低位加1得补码。

　　　比如，以一个字节来表示-3，那么[−3]原=10000011 [−3]反=11111100 [−3] 补=11111101  [−3]移=01111101

　　

举个栗子

【3.14的单精度浮点数表示】

首先将3.14转成二进制:

整数部分3的二进制是11

小数部分0.14的二进制是：0.0010001111010111000010[10001111.....]（方括号中表示小数点后第23位及之后）

这样，3.14的二进制代码就是：11.0010001111010111000010[10001111....]×2⁰

那么用正规化表示就是：1.10010001111010111000010[10001111....]×2¹

方括号表示的超出23位之后的二进制部分，由于单精度浮点数尾数只有23位，所以需要舍入（舍入方法见后）

由于第24位为1，且之后 不全为 0，所以需要向第23位进1完成上舍入：1.10010001111010111000011×2¹

而其指数是1，需要加上移码127，即128，也就是1000 0000

它又是正数，所以符号为0

综上所述，3.14的单精度浮点数表示为：
0 1000-0000 1001-0001-1110-1011-1000-011

S符号位    0 

e指数位　1000-0000

M尾数位  1001-0001-1110-1011-1000-011

十六进制代码为：0x4048F5C3

误差

　　通过栗子可知，3.14的单精度浮点数表示是0 1000-0000 1001-0001-1110-1011-1000-011。现在我们来还原，看看它的误差：

　　指数是128，那么还原回去（减去移码），实际指数就是1

　　尾数还原也就是：10010001111010111000011，所以正规化形式是：1.10010001111010111000011×2¹

　　也就是11.0010001111010111000011

　　利用二进制转十进制，可得它对应的十进制数是：3.1400001049041748046875  不等于3.14

　　这就是为什么浮点数运算结果在业务代码中总是不可确切预期的原因！！！！

机器ε

　　机器ε表示1与大于1的最小浮点数之差。例如双精度表示1和表示大于1的最小浮点数

　　

　　

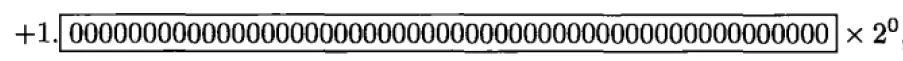
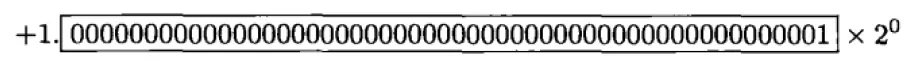
　　双精度浮点数的机器ε = 2^-52 ≈ 2.220446049250313e-16

　　同理，单精度的机器ε = 2^-23 ≈ 1.1920928955078125e-7

　　在舍入规则中，相对舍入误差不能大于机器ε的一半。

非正规化

　　  单精度浮点数为例

　　（1）0的表示

　　　　对于阶码为0或255的情况，IEEE754标准有特别的规定：

　　　　如果 阶码E=0并且尾数M是0，则这个数的真值为±0（正负号和数符位有关）。

　　　　+0的机器码为：0 00000000 000 0000 0000 0000 0000 0000

　　　　-0的机器码为：1 00000000 000 0000 0000 0000 0000 0000

　　　　需要注意一点，浮点数不能精确表示0，而是以很小的数来近似表示0。因为浮点数的真值等于

　　　　x=(−1)^S×(1.M)×2^e 

　　　　e=E−127

　　　　那么

　　　　+0的机器码真值为  1.0×2⁻¹²⁷ 

-0机器码真值为  −1.0×2⁻¹²⁷

　　（2）无穷的表示
　　　　如果阶码E=255 并且尾数M全是0，则这个数的真值为±∞（同样和符号位有关）。

　　　　因此

　　　　+∞的机器码为：0 11111111 000 0000 0000 0000 0000 0000

　　　　-∞的机器吗为：1 11111111 000 0000 0000 0000 0000 0000

　　（3）NaN（Not a Number）
　　　　如果 E = 255 并且 M 不全是0，则这不是一个数（NaN）。

舍入规则

　　以23位尾数位的单精度浮点数为例，舍入时需要重点参考第24位

　　若第24位为1，且第24位之后全部为0。此时就要使第23位为0：若第23位本来就是0则不管，若第23位为1，则第24位就要向第23位进一位，这样第23位就可以为0

　　若第24位为1，且第24位之后不全为0，则第24位就要向第23位进一完成上舍入。

　　若第24位为0，此时直接舍去不进位，称为下舍入。

再来个栗子

JavaScript console 双精度浮点数

>>9.4 - 9 - 0.4 === 0
<<false
>>(9.4-9-0.4).toFixed(20)
<<"0.00000000000000033307"

9.4-9-0.4不严格等于0，其运算结果误差。

因为按照上面的浮点数知识可知

9.4在机器内被表示为：9.4+0.2×2^-49

0.4被表示为：0.4+0.1×2^-52

当9.4-9时（因为9是整数是可以精确存储的）得0.4+0.2×2^-49，再减去0.4+0.1×2^-52得3×2^-53，约等于"0.00000000000000033307"。

 

详细解释：

9的二进制是1001，而0.4的二进制是0.0110-0110-0110-……无限循环的。从而9.4的二进制是1001.0110-0110……，正规化以后就变成 1.001-0110-0110-……×2^³，

因为双精度浮点数是52位尾数，所以小数部分保留0.001-0110-0110-……-0110-0 [110-0110-0110-……]。即001后跟12个0110循环节，然后第52位是0，中括号表示从

第53位起开始舍弃的部分。根据我提到的舍入规则，第53位1且后面不全为0，要向第52位完成上舍入，所以小数部分就变成 0.001-0110-0110-……-0110-1。至此我们

可以看到，这个数较之9.4，由于小数部分第52位由0变为1，所以多加了2^-52，但是因为从小数部分第53位开始舍弃了，舍弃部分是 0.1100-1100-…×2^-52 = 0.8×2^-52。

所以我们多加了2^-52，但是少了0.8×2^-52，这就意味着，但考虑尾数部分，这个数比9.4多了 2^-52 - 0.8×2^-52 = 0.2×2^-52，别忘记之前还有一个2^3，所以整

体多了0.2×2^-52×2^³ = 0.2×2^-49

这就是为什么9.4在机器内被表示为：9.4+0.2×2^-49

同理，0.4在机器内被表示为：0.4+0.1×2^-52