无理数的定义和实数理论的建立

本文第一版发布于2018年1月10日，第四次修订于2021年12月24日。

看完本文后你至少会明白如下几个关键问题：

无理数最初来源于几何上的发现，那为什么不采用几何的方式来定义无理数呢？是什么原因使得康托（Georg Cantor）和戴德金（Richard Dedekind）的无理数或实数定义都不采用几何的方式？用几何的方式真的不行吗？
算术法则或数学是真理吗？
什么是数的连续体？实数系为什么是连续的？
为什么无理数也有像有理数那样的乘法结合律和分配律等算术法则？如何证明？
矩形的面积为什么是两邻边长度的乘积？

我们知道有理数可以被定义成用$\frac{p}{q}$这种形式来表示的数，其中$p$是整数，$q$是正整数，有理数的加法和乘法的定义分别是：

\[\frac{a}{b} + \frac{c}{d} = \frac{ad + bc}{{bd}}\]

\[\frac{a}{b} \cdot \frac{c}{d} = \frac{{ac}}{{bd}}\]

基于此并结合已有的整数算术运算法则（Arithmetical operations，交换律、结合律、分配律等），我们就可以证明有理数也有交换律、结合律、分配律等算术法则，下面以有理数加法的交换律作证明示例：

\[\frac{a}{b} + \frac{c}{d} = \frac{ad + bc}{{bd}} = \frac{cb + da}{{db}} = \frac{c}{d} + \frac{a}{b}\]

其中第一个和最后一个等号是基于有理数加法的定义得出来的，中间的等号成立是基于整数的加法和乘法的交换律¹。

无理数在我们的运算使用中常常被认为也满足交换律、结合律、分配律等算术法则，但为什么它们也具备这些性质呢？我们同样需要严谨的证明才能信服，而这首先得从什么是无理数，从无理数的定义谈起。无理数和有理数都被称为实数，所以如果我们有了实数的定义，那么无理数的定义也可以用这个更广泛的实数定义来充当。本文将先带读者领略两种当前盛行但又过于抽象的实数定义方式，对比之下提出一种简单易懂且兼具严谨性的无理数定义，从而与有理数一起组成数的连续体——实数系，然后再严格建立起实数（包括无理数）相关的算术法则和不等关系。文中会有很多英文资料的引证，看不懂没关系，因为对应的主要意思我都在之前用中文表述了。看本文前先看柯朗和罗宾的《什么是数学》²的第二章开头至第二节的第一小节会有更好的效果。

两种定义实数的方式及其成因分析

现在让我们来看两种当今比较盛行且又独具一格³的实数定义——分别由德国数学家康托（Georg Cantor，1845－1918）的和戴德金（Richard Dedekind，1831－1916）提出。

Cantor对实数的定义⁴：实数是一个有理数的柯西数列（Cauchy sequence of rational numbers）。其中，是“有理数的柯西数列”的条件是：该数列中的各项都是有理数，并且数列中除有限多项外的其它任意两项的差都小于一个预先任意指定的正有理数。任何一个满足这种条件的数列都是有理数的柯西数列，也是这种定义下的一个实数。

现在大多数教材把Dedekind对实数的定义⁵表述为：实数是一种有理数集的Dedekind分割。其中，有理数集的Dedekind分割的定义是：把有理数集分成两个非空集合$A_{1}$和$A_{2}$，对于$a_{1} \in A_{1}$和$a_{2} \in A_{2}$有$a_{1} < a_{2}$。任何一组这样的$A_{1}$和$A_{2}$都是一种有理数集的Dedekind分割，也是这种定义下的一个实数。

当第一次看到这类实数定义时，你也许会像我一样很苦恼地感叹道：这是什么东西？如此怪异，完全看不懂！按照他们这些定义来描述实数，那么实数到底是个什么东西？完全没有了我们一开始对实数认识的样子了。之前我们可以直观地认为实数就是数轴上的第一个点，但现在，实数从我们自认为非常熟悉的东西变成了难以捉摸、令人费解的怪物！在这两种定义下，每个无理数已不再是我们之前可能认为的那样是一个单独的个体、是一个无限不循环小数，而是被定义成了和无限个元素的集合相关的东西，令初学者看了有些不知所言为何物（It is apparent from these various approaches that the logical definition of the irrational number is rather sophisticated. Logically an irrational number is not just a single symbol or a pair of symbols, such as a ratio of two integers, but an infinite collection, such as Cantor's fundamental sequence or Dedekind's cut. The irrational number, logically defined, is an intellectual monster, and we can see why the Greeks and so many later generations of mathematicians found such numbers difficult to grasp⁶）。无理数最初来源于两直角边为1的三角形的斜边长，而在这两种无理数的定义中完全看不到几何的影子，这是让初学者觉得给出的无理数定义比较抽象和怪异、难以理解的主要原因。为有理数提供严谨逻辑理论的数学家Hermann Hankel对此评论说：“各种抛弃了几何定义出来的无理数尽管有了严谨的基础，但却是极端晦涩难懂、令人反感畏惧的人造物，我们有足够的权利去怀疑这些定义的科学价值（Every attempt to treat the irrational numbers formally and without the concept of (geometric) magnitude must lead to the most abstruse and troublesome artificialities, which, even if they can be carried through with complete rigor, as we have every right to doubt, do not have a higher scientific value⁷）。”实际上即便是定义创建者之一的Dedekind也说自己看不到这种纯抽象的实数定义会带来什么优势（But what advantage will be gained by even a purely abstract definition of real numbers of a higher type, I am as yet unable to see, conceiving as I do of the domain of real numbers as complete in itself⁸）。抛弃几何后的实数定义可说已经让初学者不知所云了，如果还要按照这种路子走下去，那么后续的学习很大程度上只是应用这些定义目的不明地、淡然无味地去证明一些结论，对于理解背后的数学思想基本没什么实质性的帮助。德国数学家Paul du Bois-Reymond也表达了和我同样的观点：剥离了实数和几何关系后建立的分析学将会使得这门学科沦为折腾符号的玩意儿（A purely formalistic-literal framework of analysis which is what the separation of number from (geometric) magnitude amounts to, would degrade this science to a mere game of symbols⁹）。

那么是什么原因促使数学家们用抛弃几何的方式去定义无理数或实数呢？这得回到数学史，从为什么要为实数提供严谨的逻辑基础谈起。数学分析的严谨化导致了对严谨的实数理论的需要（The rigorization of analysis forced the realization that the lack of clarity in the number system itself had to be remedied¹⁰)。数学分析的一个非常基础的概念是极限，而仅仅在有理数集内谈论极限是有限制的，因为有理数组成的数列其极限可能是无理数，只有在有理数和无理数组成的实数系里面谈论极限才是没有限制的。有理数的定义、算术法则、不等关系（具体是哪些请看下文“实数算术法则和不等关系的建立”的后半部分）早已严格建立，而无理数或实数的严格定义及其对应于有理数的这些性质却迟迟未得到严格建立，一直到十九世纪下半叶数学家们对无理数的使用都是凭直觉进行的¹¹，默认它们也有像有理数那样的算术法则。因此，为实数提供严谨逻辑基础的问题变成了如何严谨化无理数相关的理论（By the latter part of the nineteenth century the question of the logical structure of the real number system was faced squarely. The irrational numbers were considered to be the main difficulty¹²）。

首当其冲的是要明确什么是无理数，要给无理数下个定义。无理数是通过几何发现的，其定义方式就可以考虑基于几何或不基于几何，当今较为盛行的两种定义（如上）皆选择了不基于几何的方式，是什么原因造成了这种选择呢？查阅资料后我找出了如下原因：（1）从公元前200年左右开始到大约1870年，几乎全部数学都建立在直观经验和实用的基础上¹³，也就难以避免地出现了轻易相信几何直观而得出错误结论的情况，比如曾经出现过依赖于直观的几何经验一度普遍认为连续曲线在除了一些特殊点之外的其它各点处必有切线，直到Weierstrass给出了一个处处连续但又处处不可导的函数才终结了这一错误的直观认识。Weierstrass的这一发现使得数学家们对相信直觉和借助几何辅助思考的不严谨性起了很大的警醒作用¹⁴。由于基于几何直观得到的结论有可能（也仅仅只是“可能”，并非“一定”）是不可靠的，为了严谨化数学分析，Weierstrass等数学家倾向于用数而不是几何来为微积分或数学分析奠定严谨的逻辑基础，进而就没有用几何的方式去定义无理数¹⁵、¹⁶、¹⁷。同样的原因，上述提到的实数定义的创建者Dedekind也说自己在教授“连续增长且有上界的变量必然趋近于一个极限值”时也因为一时没有别的办法而不得不通过几何直观来讲解，但他始终觉得这种做法是不严谨的，直到他为数学分析找到了纯算术化且绝对严谨的基础¹⁸。至于Cantor，他并没有在他给出实数定义的文章 Ueber die Ausdehnung eines Satzes aus der Theorie der Trigonometrischen Reihen里说明他为什么不选用基于几何的方式定义无理数¹⁹，不过Philip E.B. Jourdain认为Cantor的无理数定义是基于Weierstrass的无理数定义修改出来的²⁰，所以我们可以认为其理由和Weierstrass的一样，值得一提的是Cantor是Weierstrass的学生；（2）另外一个Dedekind认为无理数的定义应该脱离于几何的理由是：就像负数和分数的定义及其算术法则可以追溯到正整数那样，无理数也应该来源于有理数²¹；（3）非欧几何的创建和它也能用来像欧几里得几何那样准确地描述物理空间的性质，使得数学家们认识到欧几里得几何并非关于物理空间的绝对真理²²，接着数学家们甚至无法确定到底哪种几何或者几何还是不是关于物理空间的绝对真理²³（本文未加限定修饰的“几何”均指欧几里得几何或平面几何，但在本观点相关的论述处皆是泛指，下同），而之前创造的数学（包括微积分）却依赖于欧几里得几何，当时的一些数学家（包括高斯²⁴）为了避免数学因此而丧失作为自然界法则方面的真理地位（truth in the sense of laws about the real world²⁵），觉得解决之道在于把数学完全建立在算术（Arithmetic）上，因为他们在某种哲学层面上相信算术才是真理²⁶（Another motivation to erect the foundations of the number system was the desire to secure the truth of mathematics. One consequence of the creation of non-Euclidean geometry was that geometry had lost its status as truth (Chap. 36, sec. 8), but it still seemed that the mathematics built on the ordinary arithmetic must be unquestionable reality in some philosophical sense²⁷）。而数是算术的基础，这种做法就要求数在本质上不能依赖于几何。

现在让我们简短总结一下上述提到的历史上不用几何方式定义无理数的原因：（1）数学家们担心依赖于几何直观性的方式可能导致错误结论；（2）Dedekind认为就像负数和分数的定义及其算术法则可以追溯到正整数那样，无理数也应该来源于有理数；（3）倾向于认为算术而非几何是真理，这要求作为算术基础的数在本质上不能依赖于几何。然而，我认为这三条理由均不能否决“用几何方式定义无理数”的可行性。对于理由（1），的确，轻易相信几何直观确实很可能产生错误结论，但这并不意味着几何学的方式不严谨（Despite the fact that geometry too had been rigorized, one consequence of the rigorization movement was that number and analysis took precedence over geometry.²⁸），而是人们应用几何的方式是不严谨的——仅仅通过一些个案的直观性，并没有严格的证明，就草率地得出普遍性的结论。一部分数学家只是因为“相信几何直观可能产生错误结论”，为了避免这种“只是可能但并非一定会有”的风险，所以就不选用几何而是用纯数、纯算术的方式为数学奠基。更何况如果几何学是不严谨的，那么它是不是早已退出数学领域了呢？然而并未如此！对于理由（2），虽然说科学理论的发展可以受一些思想观点的指导，但它们绝非科学理论发展的枷锁或准绳，所以Dedekind的这个观点我们也就不必视为绝对要遵从的真理；对于理由（3），当时的一些数学家认为算术是真理，但是这种观点也很快受到了质疑。一方面，这种观点仅仅只是来源于有限的实践经验的认识，其正确性并没有一个严格的论证，况且当时数或算术法则连一个严谨的逻辑基础都还没有²⁹（这是本文要建立的一点）；另一方面，非交换代数（non-commutative algebras）的产生，尤其是四元数（quaternions）和矩阵（matrices）的产生，让数学家们开始反思“数或算术的应用能够在多大程度上反映客观世界的真实”，Hermann von Helmholtz (1821-1894)指出数的应用结果能符合事实的这一特性虽然不是偶然但也不能证明数的算术法则就是真理³⁰，实际上这后面的本质是：数的算术法则来源于现实生活中的一类实践经验——测量，所以再将这些总结出来的算术法则反过来应用于对应的这些场景时显然就能适用，超出这类场景可能就不适用了。比如说把两个有理数的加法$\frac{a}{b} + \frac{c}{d}$的结果定义成$\frac{ad + bc}{{bd}}$而不是$\frac{a + c}{b + d}$就是出于测量的需要，如果定义成后者就会出现$\frac{1}{2} + \frac{1}{2} = \frac{1 + 1}{2 + 2} = \frac{1}{2}$，从测量的角度来看这是个荒谬的结果³¹。另外，超出测量场景算术法则可能就不适用了，比如Henri Lebesgue举了个滑稽的例子³²：如果你把一只狮子和一只兔子放在同一个笼子里，那么最终从动物数量这个角度来看就无法得出1+1=2这个结论，类似的现象在化学里还有很多，所以算术法则的应用范围也是有限的。总的来说，数学或其它自然科学在客观世界的有效应用的本质是：它们来源于现实生活中的一类实践经验，而后再将这些总结出来的规律反过来应用于对应的场景时显然就能适用，超出这类场景可能就不适用了。之所以说是来源于生活中的“一类”或“有限”实践经验，其决定性原因是除非是造物者（God）否则谁都不敢保证自己的理论是在考量完生活中的所有相关情况之后提出的，另一方面，理论提出后谁都不敢说自己核实完世间一切相关情形证明理论总是适用，只能保守地说理论适用于与之相应的场景，更别说生活中已发现理论不再适用的情形了（如上面算术法则失效的例子），所以这些提出来的理论只不过是应用范围有限的经验知识，其应用范围取决于实践认识。此外，当有经验或实验显示另外一种新的理论可以提供更好的解读时，那么旧理论很可能就会被这个新理论取而代之（Some areas of experience suggest particular sets of axioms and to these areas the axioms and their logical consequences apply accurately enough to be taken as a useful description. But if any area is enlarged the applicability may be lost. As far as the study of the physical world is concerned, mathematics offers nothing but theories or models. And new mathematical theories may replace older ones when experience or experiment shows that a new theory provides closer correspondence than an older one.³³）。所以，就如休谟（David Hume，1711-1776）所说：一切科学理论都是基于（有限）经验建立起来的（Science is purely empirical³⁴）。所谓的自然法则全是人类创造的，是我们人类而不是造物者给出了这些法则，所以每条自然法则只不过是人类的解读，不见得是造物者的意思——绝对真理（Nature's laws are man's creation. We, not God, are the lawgivers of the universe. A law of nature is man's description and not God's prescription.³⁵）。所以，继几何之后认识到算术也不是关于客观世界的绝对真理³⁶我们就会认识到历史上“让数的定义脱离于几何，然后就相信基于数的算术或数学是真理”的做法便不具备什么意义了，相反我们更应该认识到数和几何的紧密联系，比如有理数的加法和乘法定义实际上是源于（几何）度量的需要定义出来的³⁷，一个更迫切的需求是：我们需要每条线段的长度都要能用一个数去代表、去衡量，这也是分析几何（Analytic geometry）的基本要求。实际上即便是上面这两种实数定义的提出者Cantor和Dedekind——他们用抛弃了几何的方法去定义实数，但是为了在“数（特指实数集）”和“形（特指直线）”之间建立联系也不得不用公理化的方式说明他们所定义的实数和直线上的每个点是一一对应的³⁸（后世称之为Cantor-Dedekind公理³⁹）。正是基于“数”和“形”之间无法割舍的紧密关系，也因为并不是非得用抛弃几何的方式去定义实数，更何况这么定义的实数非常抽象和怪异、不易理解，所以本文将基于几何（直线）建立一种简单易懂且兼具严谨性的无理数定义方式，然后再建立起与之相关的算术法则和不等关系。

本文的无理数或实数定义、数的连续体

首先我们来看如何把所有的有理数表示在一条直线上。在一条水平直线上选定代表0和1的点之后（0在1的左边），把0和1间的距离叫作单位长度，在1的右边每隔一个单位长度就取一个点，一直无止境地进行下去，把这些新标示出来的点从左到右依次用来代表2，3，4……这些正整数，在0的左边每隔一个单位长度就取一个点，一直无止境地进行下去，把这些新标示出来的点从右到左依次用来代表-1，-2，-3，……这些负整数，这样我们就在这条直线上找到了代表每个整数（分母为1的有理数）的点，可以通过尺规作图来完成这种构造。每个有理数都可以用$\frac{p}{q}$这种形式唯一表示，其中$p$是整数，$q$是正整数，并且$p$和$q$没有比1大的公因子，为了在这条直线上标出代表分母$\mathbf{q}$大于1的有理数的点，我们只需把每个单位长度的区间进行$q$等分（尺规作图可以做到这一点⁴⁰），那么每一个分点就都代表一个分母为$q$的有理数。显然每个有理数都可以用这种方法在理论上于这条直线上找到代表它的那个点，可称这些点为“有理点”、这条直线为数轴。值得注意的是这条直线上的所有点并非都是有理点，比如用圆规以两直角边为1的三角形的斜边长为半径，代表0的点为圆心画圆的话，那么圆弧与这条直线在0的右边的交点就不会与任何有理点重合（如图所示）⁴¹。

$C:\Users\i\Desktop\12_看图王.png$

其证明可用反证法：假设交点与一有理数$\frac{p}{q}$相对应，也即直角三角形的斜边长度为$\frac{p}{q}$，那么根据勾股定理有$1^{2} + 1^{2} = ({\frac{p}{q})}^{2} = 2$。按规定$p$和$q$没有比1大的公因子，把等式(${\frac{p}{q})}^{2} = 2$稍作变换得到$p^{2} = 2q^{2}$，那么$p^{2}$就是偶数了，显然$p$也必须是偶数，便有$p = 2p_{0}$，$p_{0}$是整数，把前面等式的$p$换作$2p_{0}$就有$4p_{0}^{2} = 2q^{2}$，即$2p_{0}^{2} = q^{2}$，这说明$q^{2}$是偶数，显然$q$也必须是偶数，于是$p$和$q$有公因子2，这与前面“$p$和$q$没有比1大的公因子” 的规定矛盾，而造成这种矛盾的起因就是我们一开始假设那个交点是有理点，所以数轴上的点并非都有有理数与之对应，可称没有有理数与之对应的点为“无理点”，很容易在数轴上构造出无数多个无理点出来。

如果从形式上来看的话，那么有理数只是可以写作$\frac{p}{q}$这种形式的符号。有理数和数轴上的有理点一一对应，并具备一些算术法则和不等关系。根据使用需要，我们有必要引入另外一组符号来与数轴上所有的无理点一一对应，可把这每一个与无理点相对应的符号都称为“无理数”⁴²，为了使用这些符号，我们希望它们也具备像有理数那样的算术法则和不等关系——这是下文的要建立的。如果一个点在另外一点的右边，那么称与这个点对应的数$x$大于与左边那个点对应的数$y$，记为$x > y$，反之则是“小于”，记为$x < y$。至此，各位应该掌握到的是：本文定义无理数为数轴上与无理点相对应的一个符号，此外数与数之间有这种大小关系。可把已经有的有理数和这里新引入的无理数统称为实数（把所有的实数称为实数集或实数系），这样实数就和数轴上的点一一对应了。

直线是连续的，其连续性表现出了这样的性质：“如果把一条水平直线上的所有点分成左右两个部分，那么其中有且仅有一个点能造成这种分割，并且这个点是左边这部分的最后一点或右边这部分的起点。”如果假设其中至少有两个不同点可以把直线分成同样的左边和右边两部分，那么这两个点间的那无数多个点既不同时属于这两个点产生的分割的左边部分也不属于右边部分，因此“有且仅有一个点能造成这种分割”，这条性质是由德国数学家戴德金（Richard Dedekind）提出的⁴³，他认为这是一个明显的事实，无需也无法被证明，它能够刻画直线的连续性，它是直线之所以连续的本质体现，应将其看作一条公理⁴⁴，可称其为直线连续性公理（line continuity axiom）。

实数集里的实数可以和直线上的点一一对应，再加上我们也定义了任意两个实数的大小关系，所以实数集里也同样可以提出与直线连续性公理相应的性质：如果把实数集内的所有数分成两部分$A_{1}$和$A_{2}$，以至于$A_{1}$内的每个数都小于$A_{2}$内的每个数，那么其中有且仅有一个数能产生这个分割，并且这个数是$A_{1}$这部分的最大数或$A_{2}$这部分的最小数⁴⁵——这应该看作是实数集连续性的本质表现，因为这条性质是受直线连续性公理启示而提出来的，所以也应将它看成是一条公理。实数集，因为具备连续性，所以也被称为数的连续体，英文number continuum⁴⁶，亦译作“数的连续统”，这条描述其连续性的公理可称为数的连续体公理（number continuum axiom）。

有理数集便不具备这样的连续性。例如上述我们已经证明过没有平方等于2的有理数，所以可把有理数分成所有负有理数和平方小于2的非负有理数组成的集合$A_{1} = \{ x \in \mathbb{Q}|x^{2} < 2{\ or\ }x < 0\}$和所有平方大于2的正有理数组成的集合$A_{2} = \{ x \in \mathbb{Q}|x^{2} > 2{\ and\ }x > 0\}$，$A_{1}$内的每个数都小于$A_{2}$内的每个数，但这时有理数集内就没有一个数能产生这个分割。如何证明呢？假设有一个有理数$a$能产生这个分割，那么根据数的连续体公理可知这个数是$A_{1}$这部分的最大数或$A_{2}$这部分的最小数。假设$a$是$A_{1}$内最大的有理数，那么$a$必然是正有理数，只要选定足够大的正整数$n$就可以让$a + \frac{1}{n}$变得比$a$稍大一点点，那么会不会存在正整数$n$使得$\left( a + \frac{1}{n} \right)^{2} < 2$呢？若存在，那么我们便说明了$A_{1}$内有比$a$更大的有理数$a + \frac{1}{n}$，从而说明$A_{1}$内无最大的有理数。因为$\left( a + \frac{1}{n} \right)^{2} = a^{2} + \frac{2a}{n} + \frac{1}{n^{2}} < a^{2} + \frac{2a}{n} + \frac{1}{n} = a^{2} + \frac{1}{n}(2a + 1)$，如果能证明存在正整数$n$使得$a^{2} + \frac{1}{n}(2a + 1) < 2$，那么$\left( a + \frac{1}{n} \right)^{2} < 2$自然得证。对$a^{2} + \frac{1}{n}(2a + 1) < 2$稍作变形可得$\frac{1}{n} < \frac{2 - a^{2}}{2a + 1}$ ，现在问题变成了是否存在正整数$n$使得$\frac{1}{n} < \frac{2 - a^{2}}{2a + 1}$ ，因为$a$是正有理数且$a^{2} < 2$，所以$\frac{2 - a^{2}}{2a + 1}$是正有理数，根据有理数的阿基米德性质⁴⁷（对于任何正有理数，总存在正整数$n$使得$\frac{1}{n}$小于它）知存在这样的正整数$n$，也就存在正整数$n$使得$\left( a + \frac{1}{n} \right)^{2} < 2$，所以$A_{1}$内无最大的有理数。用类似的方法也可以证明$A_{2}$内无最小的有理数。所以，有理数集不具备连续性。

现在的数学分析教材里基本上都是用另外一条与数的连续体公理等价的公理来刻画实数系的连续性——非空有上界的实数集在实数集内有最小上界（上确界），称为实数集的最小上界公理（Least Upper Bound Axiom⁴⁸）。有需要的读者请先去了解实数集的这些概念以便继续阅读：上界、最小上界（亦作“上确界”，英文the least upper bound）、下界、最大下界（亦作“下确界”，英文the greatest lower bound）。首先让我们来看如何通过“数的连续体公理”推导出“实数集的最小上界公理”，具体来讲是在有“数的连续体公理”和“实数集的非空且有上界的真子集A”的情况下，证明A在实数集内有最小上界d，证明过程：把比A内每个数都大的实数归拢到集合C，余下的实数组成的集合B（显然B里面的每个数都小于C内的每个数），根据数的连续体公理可知有且仅有一个实数d能把实数集分成B和C两部分，d是B的最小上界。因为A⊂B，所以B的上界就是A的上界，又因为集合B内的每个数不都大于A内每个数，所以A的上界就是B的上界，综上可知集合A和集合B有共同的最小上界d，所以非空且有上界的集合A在实数集内有最小上界；再看如何通过“实数集的最小上界公理”导出“数的连续体公理”，具体来讲是在有“实数集的最小上界公理”和“实数集内的所有数被分成两部分$A_{1}$和$A_{2}$，并且$A_{1}$内的每个数都小于$A_{2}$内的每个数”的情况下，证明$A_{1}$这部分有最大数或$A_{2}$这部分有最小数，证明过程：$A_{1}$显然有上界，根据实数集的最小上界公理可知它在实数集内有最小上界d，这时候d要么在$A_{1}$内并且是里面的最大数，要么在$A_{2}$内并且是里面的最小数，否则便会与它是最小上界的结论相悖。所以，数的连续体公理和实数集最小上界公理是等价的，它们表述的都是实数系连续性这一实质。实际上这里从“数的连续体公理”或“实数集的最小上界公理”被推导出的角度来看我们就不能用“公理”来称它了，应该叫作“定理”更准确，实数集的连续性也被称为实数集的完整性（或完备性）公理（或定理）（completeness axiom 或completeness theorem），至于叫它公理还是定理同样取决于是否将其看作是给定的事实。

实数的加减乘除定义

为实数系建立严谨逻辑基础的核心问题是如何定义无理数及建立起与之相关的算术运算法则和不等关系。行文至此，本文的无理数定义我们已经有了——数轴上与无理点相对应的一个符号，接下来要做的就是建立起与无理数相关的性质。同样地，如果我们能够建立起实数间的算术运算法则和不等关系，那么无理数的这些性质也就无形中被从这个更大的层面建立了。

首先要建立的是实数集的阿基米德性质，为此有必要先建立实数间的加法、减法、任意实数乘以或除以正整数n这三种运算的结果，定义的方法同样依赖于几何，我将用尺规作图的方式进行展示。首先来看如何用尺规作图定义两个实数的加减法的结果，此处以两个正实数a、b为例：以正数a在数轴上所代表的点为圆心，以原点到正数b的长度为半径，用圆规画弧与数轴在a点右方的交点即为实数a+b的结果，在a点左方的交点为a-b的结果。当a或b为负数的时候，也能很容易地调整后构造出a+b或a-b的结果，此处不再敖述。

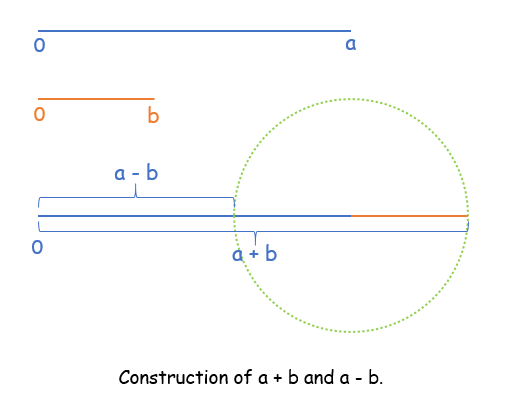
很显然我们也能构造出任何实数a的n倍，即na。a的$\frac{1}{n}$，即$\frac{a}{n}$也是可以通过尺规作图在数轴上构造出，上文也提到过，愿闻其详者请看这里。另外我们还需要再引入几条实数系内的公理：（1）若x≤y，则x+z≤y+z；（2）若0≤x≤y，则nx≤ny和$\frac{x}{n}$≤$\frac{y}{n}$。这样我们就有基础建立下面的性质了。

实数集的阿基米德性质（Archimedean Property for Real Numbers）：如果x和y都是任意正实数，尤其是 x<y时，总存在正整数n使得nx > y.

可用反证法来证明：假设nx > y对于任何正整数n都不成立，那么也就是说集合A={nx|n∈N}有上界y。根据实数集的最小上界性质可知A有最小上界z，因为x是正数，所以z-x就不是A的上界，那么也就存在正整数m使得在A内有mx>z-x，该式两边都加上x后有mx+x>z，即（m+1）x>z，也就是A中有元素（m+1）x大于A的最小上界，这与最小上界的定义相悖，所以原结论得证⁴⁹。

根据实数集的阿基米德性质可得到如下两条性质：

（1）对于任意正实数x，总存在正整数n使得$\frac{1}{n} < x$。

将不等式两边都乘以n得到1<nx，所以问题变成了：对于任意正实数x，是否总存在正整数n使得1<nx？根据上述实数集的阿基米德性质可知这样的正整数n总是存在的，故本条性质得证。

实际上到这里我们便具备给出函数或数列极限的(ε, N)定义的基础了，但为了避免增加不必要的复杂性，故此略去，要说明的是本条性质对于在实数系内证明数列$a_{n} = \frac{1}{n}$ 的极限为0是极为关键的。因为当n变得越来越大的时候，$\frac{1}{n}$变得越来越小，从图像上来看$\frac{1}{n}$也是在越来越接近0，但无论n有多大，$\frac{1}{n}$始终大于0，所以会不会有正数比所有的$\frac{1}{n}$都小但又大于0呢？根据本条性质就可以否定这个问题。

通过实数集的阿基米德性质和本条性质可知：（2）实数集内即无最大正数也无最小正数。

上面我们已经建立了实数间的加法、减法，而乘除法的建立需要我们先明了如下这部分内容：对于数轴上的任意一点$x$至少有一个整数$c_{0}$使得

\[c_{0} \leq x \leq c_{0} + 1,\]

换句话说$x$属于闭区间$I_{0} = \left\lbrack c_{0},c_{0} + 1 \right\rbrack$，将$I_{0}$十等分，则其间新产生的9个分点分别是$c_{0} + \frac{1}{10},c_{0} + \frac{2}{10},\ldots,c_{0} + \frac{9}{10}$，$x$至少会在这新产生的其中一个小区间上，也就是

\[x \in I_{1} = \left\lbrack c_{0} + \frac{1}{10}c_{1},c_{0} + \frac{1}{10}c_{1} + \frac{1}{10} \right\rbrack\]

其中$c_{1} \in \left\{ 0,1,2,\ldots,9 \right\}$。如果$x$碰巧是上述9个分点之一的话，那么它可以属于以其为左端点的小区间，也可以属于以其为右端点的小区间，每逢这种情况，为了避免随之而来的不必要的复杂性，我们一律限定$x$属于以其为左端点的小区间（补充一点：上述$c_{0}$我们也作类似的处理），后面我们会看到这种选择带来的便利之处。接着将$I_{1}$也十等分，同样有

\[x \in I_{2} = \left\lbrack c_{0} + \frac{1}{10}c_{1} + \frac{1}{100}c_{2},c_{0} + \frac{1}{10}c_{1} + \frac{1}{100}c_{2} + \frac{1}{100} \right\rbrack\]

显然，重复上述步骤到第$n$次时有

\[x \in I_{n} = \left\lbrack c_{0} + \frac{1}{10}c_{1} + \cdots + \frac{1}{10^{n}}c_{n},c_{0} + \frac{1}{10}c_{1} + \cdots + \frac{1}{10^{n}}c_{n} + \frac{1}{10^{n}} \right\rbrack\]

$c_{1},c_{2},\ldots\ ,c_{n}$ 均是$0,1,2,\ldots,9$中的其中一个，闭区间$I_{n}$的长度是$\frac{1}{10^{n}}$。如此无止境地构造下去便会得到无限多个区间

\[I_{1},I_{2},\ldots,I_{n},\cdots\]

其中后一个都包含在前一个内，各区间的长度$10^{- 1},10^{- 2},10^{- 3},\ldots$也在越来越靠近0。对于这无限多个$I_{n}$有两点需要说明：（1）$x$在每个$I_{n}$上——毕竟这是我们构造各个$I_{n}$的要求；（2）除$x$外没有其它的数始终包含在这无限多个$I_{n}$上。为了证明这一点，我们可以用反证法：假设除了$x$外还有另外一个数$y$在这无限多个$I_{n}$上，要使$y$和$x$都在每个$I_{n}$上，就要求二者的差值不大于各个区间的长度$\frac{1}{10^{n}}$，也就是要求$|y - x| \leq \frac{1}{10^{n}}$对于一切正整数$n$成立，这个不等式可以变换为$10^{n}|y - x| \leq 1$，这与阿基米德性质相悖，所以这无限多个$\mathbf{I}_{\mathbf{n}}$可以界定唯一一个数。当n越大时，各个$I_{n}$的左右端点都只会唯一逼近$x$，而这无限多个$I_{n}$的左右端点都是有理数，所以这一事实可以简化为：这无限多个$I_{n}$的左端点构成的有理数数列唯一逼近$x$。

记逼近$a$的这无限多个$I_{n}$的左端点有理数构成的数列为$\left\{ a_{n} \right\}$，记逼近$b$的这无限多个$I_{n}$的左端点有理数构成的数列为$\left\{ b_{n} \right\}$。当n越来越大的时候，$a_{n}$会唯一逼近$a$，$b_{n}会唯一逼近b$，那么数列$\left\{ a_{n} + b_{n} \right\}$显然会唯一逼近$a + b$，$\left\{ a_{n} - b_{n} \right\}$显然唯一逼近$a - b$，不过我们不能说可以用$\left\{ a_{n} + b_{n} \right\}$和$\left\{ a_{n} - b_{n} \right\}$来定义实数$a$和$b$的加减法，其原因是数列$\left\{ a_{n} \right\}$和$\left\{ b_{n} \right\}$的得来依赖于“这无限多个$I_{n}$可以唯一界定一个数”，这条性质的建立需要用到实数集的阿基米德性质，而阿基米德性质的建立又需要我们提前有实数间的加减法定义，上述早已采用了几何方式定义了加减法，不过通过这种数列逼近的方式来处理数量关系方面的问题会很方便（见下文）。在此补充说明两点：（1）本文所说的“逼近”、“唯一逼近”、“唯一界定”实际上就是极限，与之相关的表述都可以用极限的(ε, N)定义进行严格证明，为了避免引入过多的符号演算对数学思想传递起到掩盖或阻碍的副作用，故此略去这部分证明，想深究的读者可用这种方法去求证；（2）逼近$x$的这无限多个$I_{n}$的左端点有理数构成的数列的各项均是$c_{0} + \frac{1}{10}c_{1} + \cdots + \frac{1}{10^{n}}c_{n}$这种形式，如果我们简记其为$c_{0.}c_{1}c_{2}c_{3}\cdots c_{n}$，那么就得到了逼近$x$的有理数数列各项的“十进制小数”表示方式，进一步我们用$c_{0.}c_{1}c_{2}c_{3}\cdots c_{n}\cdots$表示这一系列小数的极限（结尾的省略号表示$c_{n}$后面还有无限多个数位），换句话说每个实数都可以写作这种形式。上面说到本文的每个无理数都被定义成和数轴上的无理点对应的一个符号，但并没有说这个符号具体是怎样的形式，从实数的十进制小数表示方式这个角度来看每个无理数都可以记作$c_{0.}c_{1}c_{2}c_{3}\cdots c_{n}\cdots$这种形式的符号。深入了解实数的十进制小数表示方式可看From Numbers to Analysis, Inder K. Rana, p255-260和Terence Tao, Analysis I, third edition, Chapter B, Appendix: the decimal system。

$a$和$b$的乘除法还有待定义，你可能已经想到：可以考虑用数列$\left\{ a_{n}b_{n} \right\}$和$\left\{ \frac{a_{n}}{b_{n}} \right\}$唯一逼近的值来分别定义$a \cdot b$和$\frac{a}{b}$、来作为$a \cdot b$和$\frac{a}{b}$的结果，但是除非我们能在不用到$a \cdot b$和$\frac{a}{b}$的情况下证明$\left\{ a_{n}b_{n} \right\}$和$\left\{ \frac{a_{n}}{b_{n}} \right\}$都有极限、都分别唯一逼近一个数，否则比如说在未定义$a \cdot b$的情况下证明$\left\{ a_{n}b_{n} \right\}$有极限的过程中如果用到${ab}$（例如出现$\left| a_{n}b_{n} - ab \right| < \varepsilon$）就犯了循环论证（circular reasoning）的错误⁵⁰。为了在没有定义$a \cdot b$和$\frac{a}{b}$的情况下证明$\left\{ a_{n}b_{n} \right\}$和$\left\{ \frac{a_{n}}{b_{n}} \right\}$都有极限，我们需要引入柯西收敛准则（Cauchy's Convergence Criterion），而这有必要从极限点（limit point）说起。

对于数列${\{ x}_{n}\}$，如果每个包含实数x的开区间都包含无数多个$x_{n}$，那么x就是该数列的一个极限点。根据这个定义，如果一个数列有极限，那么因为每个包含极限值的开区间几乎包含了数列的所有项（各开区间外只有数列的有限项），所以极限值就是一个极限点，反过来看，如果每个包含极限点x的开区间几乎包含了数列里的所有项（各开区间外只有数列的有限项），那么根据数列极限的(ε, N)定义可知极限点x就是该数列的极限。如果数列${\{ x}_{n}\}$有上下界，那么至少可以在其中找到一个极限点，为了说明这一点，首先我们取包含该数列所有项的区间$\lbrack y_{1},z_{1}\rbrack$，然后将其二等分，记其中一个包含该数列无限多项的区间为$\lbrack y_{2},z_{2}\rbrack$，无止境地重复这种操作我们将会得到无限多个$\lbrack y_{n},z_{n}\rbrack$，应用类似于上述证明“无限多个$I_{n}$可以唯一界定一个数”的方法，我们可以证明这无限多个$\lbrack y_{n},z_{n}\rbrack$也可以唯一界定一个数——它就是一个极限点⁵¹。有了这些基础知识之后我们就可以来证明柯西收敛准则（Cauchy's Convergence Criterion⁵²）：数列${\{ x}_{n}\}$收敛的充分必要条件是对于任意给定的正数$\varepsilon$，在该数列中总存在某N项后的任意两项$x_{m}$和$x_{n}$有$\left| x_{m} - x_{n} \right| < \varepsilon$。我们先证明其必要性：如果数列${\{ x}_{n}\}$收敛于x，那么存在某N项后的任意两项$x_{m}$和$x_{n}$分别和x的差值小于$\frac{\varepsilon}{2}$，进而$x_{m}$和$x_{n}$的差值就会小于$\varepsilon$，也就是数列收敛时存在某N项后的任意两项$x_{m}$和$x_{n}$有$\left| x_{m} - x_{n} \right| < \varepsilon$。再反过来证明充分性：因为$\varepsilon$是可以任意指定的正数，所以不妨指定$\varepsilon = 1$，根据条件可知某N项后的任意两项$x_{m}$和$x_{n}$有$\left| x_{m} - x_{n} \right| < 1$，不妨固定$x_{m}$，为了便于区分可记其为$x_{M}$，那么在该数列的某N项后有任意的$x_{n}$和$x_{M}$使得$\left| x_{M} - x_{n} \right| < 1$，也即第N项后的所有$x_{n}$都可以被限定在以$x_{M}$为中心半径为1的开区间内，进一步我们可以找到一个足够大的区间将数列的前N项也包含在其间，这样我们就看到数列${\{ x}_{n}\}$是有上下界的，所以它至少有一个极限点x，在每一个包含x的开区间内总有数列里足够靠后的一项，再根据条件该数列足够靠后的任意两项的差值是可以小于任何指定正数，所以在每一个包含极限点x的开区间内都几乎包含该数列所有的项（各开区间外只有数列的有限项），根据上述极限点和极限的关系可知x就是该数列的极限。至此，柯西收敛准则得证。

让我们回到两个实数的乘除法定义上来。如果数列${\{ a}_{n}\}$收敛于$a$，那么根据柯西收敛准则可知对于数列${\{ a}_{n}\}$里足够靠后的两项$a_{m}$和$a_{n}$，它们的值是非常接近的，同样，如果数列${\{ b}_{n}\}$收敛于$b$，那么数列${\{ b}_{n}\}$里足够靠后的两项$b_{m}$和$b_{n}$也是非常接近的，因此$a_{m}b_{m}$和$a_{n}b_{n}$的值也就非常接近，也就是数列$\left\{ a_{n}b_{n} \right\}$满足柯西收敛准则，我们把$a$乘以$b$的结果定义为它的极限，并记这个极限值为$a \cdot b$或${ab}$，也就是说我们通过数列$\left\{ a_{n}b_{n} \right\}$的极限定义了$a$乘以$b$，应用类似的方法我们可以把$a$除以$b$的结果定义为数列$\left\{ \frac{a_{n}}{b_{n}} \right\}$的极限值，记为$\frac{a}{b}$，当然定义除法的前提是要求$b \neq 0$。

至此，我们已经定义了$a$和$b$的乘除法，但是$a \cdot b$和$\frac{a}{b}$各自又有着哪些实际意义呢？对此我们心中不免还是没底，下面从矩形面积的角度解释$a \cdot b$的意义。首先我们定义边长为单位长度的正方形的面积为单位1, 如果边的长度单位是${cm}$，则对应的面积单位就定义成$cm^{2}$，单位是毫米（mm）、分米（dm）、米（m）、千米（km）等也可以作相应的定义，此处不再赘述。封闭区域内的面积是用该区域包含多少个面积为单位1的正方形来计量的⁵³。如果矩形两条邻边的长度分别是$a$和$b$个单位长度，也就是$a$和$b$都是正整数，那么矩形面积就是$a \cdot b$个单位1（这个结论的合理性如下图所示）, 或者简单地说面积等于乘积${ab}$。

$C:\Users\i\Pictures\Area-Rectangle-Demonstration.jpg (1040×720).jpg$ ⁵⁴

如果相邻两边$a$和$b$都是有理数，我们把$a$和$b$表示为$a = \frac{m}{n},b = \frac{m^{\ ^{'}}}{n^{\ ^{'}}}$，其中$m,n,m^{\ ^{'}},n^{\ ^{'}}$都是正整数，取两条边的共度单位（common measure unit）$\frac{1}{N} = \frac{1}{nn^{\ ^{'}}}$，就有$a = mn^{\ ^{'}} \cdot \frac{1}{N},b = nm^{\ ^{'}} \cdot \frac{1}{N}$，然后就可以把要求面积的这个矩形看成是由$mn^{\ ^{'}} \cdot nm^{\ ^{'}}$个边长为$\frac{1}{N}$的小正方形组成的，由于每个的面积是$\frac{1}{N^{2}}$（将面积为单位1的正方形的长和宽都N等分，那么这个正方形就被等分成了$N^{2}$个边长为$\frac{1}{N}$的小正方形，显然每个小正方形的面积就是面积为单位1的正方形的$\frac{1}{N^{2}}$），所以该矩形的面积就是$nm^{\ ^{'}}mn^{\ ^{'}} \cdot \frac{1}{N^{2}} = \frac{m}{n} \cdot \frac{m^{\ ^{'}}}{n^{\ ^{'}}} = a \cdot b$，所以相邻两边$a$和$b$都是有理数的矩形其面积仍然是${ab}$；如果$a$或$b$是无理数，那么根据我们上述唯一界定任何实数的构造方法可以分别找到形如$c_{0} + \frac{1}{10}c_{1} + \cdots + \frac{1}{10^{n}}c_{n}$的有理数数列${\{ a}_{n}\}$和$\{ b_{n}\}$分别唯一逼近$a$和$b$，换句话说我们可以找到一系列边长分别为有理数$a_{n}$和$b_{n}$的矩形去无限地近似代表要求面积的矩形，根据上一条结论“两邻边为有理数长度的矩形其面积等于这两个有理数的乘积”知道这每个矩形的面积就是$a_{n}b_{n}$，当$a_{n}$和$b_{n}$分别唯一逼近$a$和$b$时，其所代表的矩形也就唯一逼近两邻边为$a$和$b$的矩形，所以这一系列矩形面积的数列${\{ a}_{n}b_{n}\}$的极限就是两邻边至少有一边是无理数时的矩形面积，而这个极限根据前面对乘法的定义是${ab}$。综上所述，矩形的两邻边长度$a$或$b$无论是有理数还是无理数，其面积都是${ab}$ ⁵⁵。这样我们就通过矩形面积的方式赋予了${ab}$实际意义，至于$\frac{a}{b}$的实际意义，我们可以理解为是边长为$a$和$\frac{1}{b}$的矩形的面积，亦或$\frac{a}{b}$的定义使得一个实数除以另外一个非零实数的运算变得可行，当然也可以作别的合理解释，这里就不再继续探求了。

实数算术法则和不等关系的建立

在定义了实数的加减乘除法后，可以进一步证明有理数的一些算术法则和不等关系在实数范围内（尤其是无理数参与时）也仍然成立。我们可以基于上述展示的逼近实数的有理数数列来入手证明，这里给出几个证明示例。“对于有理数$a,b$，有$a \cdot b = b \cdot a$”，为了证明它在实数范围内（即当$a$和$b$都是实数时）也成立，我们考虑逼近等式左右两边的有理数数列$\left\{ a_{n}b_{n} \right\}$和$\left\{ b_{n}a_{n} \right\}$，根据有理数乘法交换律有$a_{n}b_{n} = b_{n}a_{n}$，也就是左右两边的数列对应各项都相等，逼近的就都是同一个数，故此我们就基于有理数的乘法交换律建立起了实数乘法交换律。同样地，“对于有理数$a、b、c$，$(a + b) \cdot c = a \cdot c + b \cdot c$” 为了证明它在实数范围内也成立，我们考虑逼近等式左右两边的有理数数列$\left\{ (a_{n} + b_{n}) \cdot c_{n} \right\}$和$\left\{ a_{n}c_{n} + b_{n}c_{n} \right\}$，根据有理数的乘法分配律知道这两个数列的对应各项都相等，所以它们的极限自然相等，这样我们就通过有理数的乘法分配律建立起了实数的乘法分配律。有理数范围内成立的一些不等关系也可以用类似的方法推广到实数范围内，如“对于有理数$a、b、c$，如果$a \leq b$并且$c \geq 0$，那么${ac} \leq {bc}$”可以推广到$a、b、c$为实数时，${ac} \leq {bc}$仍然成立，证明：因为$a \leq b$，所以对于如上构造出来的分别唯一逼近a和b的两个有理数数列$\left\{ a_{n} \right\}$和$\left\{ b_{n} \right\}$的每一项都有${a_{n} \leq b}_{n}$（如果不用我们上述构造的这种数列的话，那么我们只能说对于足够大的N，存在n>N使得${a_{n} \leq b}_{n}$，在我们的构造下就不需要这种约束条件），记唯一逼近c的数列为$\left\{ c_{n} \right\}$，因为$c \geq 0$，所以同样地在我们构造下数列的各项$c_{n} \geq 0$，由于有理数数列$\left\{ a_{n}c_{n} \right\}$和$\left\{ b_{n}c_{n} \right\}$分别逼近${ac}$和${bc}$，再结合前面分析出来的条件可得出${a_{n}c_{n} \leq b}_{n}c_{n}$，所以就有${ac} \leq {bc}$，因此这个不等关系在实数范围内依然成立。总的来说，我们希望实数之间（尤其是无理数参与时）也像有理数那样具备如下算术法则和不等关系⁵⁶：

对于任意给定的实数$x,y,z$，

$x \leq x$.
若 $x \leq y$ 且 $y \leq x,$ 则 $x = y$.
若 $x \leq y$ 且 $y \leq z,$ 则 $x \leq z$.
不是$x \leq y$ 就是 $y \leq x$.
若 $x \leq y,$ 则 $x + z \leq y + z$.
若 $x \leq y$ 且 $0 \leq z,$ 则 $x \cdot z \leq y \cdot z$.
$x + (y + z) = (x + y) + z$.
$x + 0 = 0 + x = x$.
对于$x$总有$y$使得$x + y = y + x = 0$.
$x + y = y + x$.
$x \cdot (y \cdot z) = (x \cdot y) \cdot z$.
$x \cdot 1 = 1 \cdot x = x$.
若$x \neq 0$，总有$y$使得$x \cdot y = y \cdot x = 1$.
$x \cdot y = y \cdot x$.
$x \cdot (y + z) = x \cdot y + x \cdot z$.

对于上述1~15条性质，觉得非常显然的可以把它当作公理，不那么一目了然的可以用上述展示的方法在有理数的基础上推广过来。1~5条是很显然的，可以当作公理。 6~15条，其中第6、14、15条我们在上面已经证明过，其余的也可以用类似的方法证明。在证明第8条和第12条的时候，得益于我们前面的两个选择（其一，在十等分区间寻求下一个$I_{n}$时，如果$x$碰巧是区间内的9个分点之一的话，那么一律限定$x$属于以其为左端点的小区间；其二，逼近$x$的数列取的是这无限多个$I_{n}$的左端点有理数构成的数列），所以这里取到的分别逼近0和1的有理数数列的各项分别都是0和1，而一个有理数与0或1的加法和乘法是极其简单的，这就使得我们在有理数的基础上把这两条性质推广到实数范围内变得很容易，另外一种能够借助这种运算上的方便的做法是在上述两处选择时都取右端点才会导致取到各项分别是0和1的有理数数列，其它选择方式都会让证明过程不再那么简单；对于第9条，根据我们上面对加法的定义很容易得出$y$是与$x$关于原点对称的那一个数；对于第13条，可以证明在如上述我们的构造下逼近$x$的不为零的各有理数依次组成的数列$\{ x_{n}\}$的各项的倒数组成的数列{$y_{n}\}$满足柯西收敛准则，不妨记这个极限为 $y$，现在我们无法直接求出$x \cdot y$的结果，但是根据本文对乘法的定义$x \cdot y$实际上就是$\{ x_{n}y_{n}\}$的极限，所以$x \cdot y = \lim_{n \rightarrow \infty}(x_{n} \cdot y_{n}) = \lim_{n \rightarrow \infty}\left( x_{n} \cdot \frac{1}{x_{n}} \right) = 1$，此$y$即为所求。

综述

乍看之下本文的实数系及其算术法则和不等关系是基于有理数和直线连续性而建立的，但深究有理数的算术法则和不等关系的来源后会发现实际上它们也是基于线段长度的度量和比较而创建的⁵⁷，所以本文的实数系及其理论是在直线连续性、线段长度度量和比较的基础上建立起来的（The problem was to interpret the geornetric property of the line:‘a continuum of points' to be phrased in terms of arithrnetic rules. ⁵⁸）。

至此，本文就基于几何通过一种简单直观且兼具严谨性的方式定义了无理数——和数轴上的“无理点”唯一对应的一个符号，所有这些符号和有理数集组成的实数集有数的连续体公理（或最小上界公理）及其推导出来的阿基米德性质，这些实数也满足有理数所具备的算术法则和不等关系。

What Is Mathematics? Second Edition, Courant and Robbins, p54↩︎
What Is Mathematics? Second Edition, Courant and Robbins↩︎
Julian Havil, The Irrationals, p241↩︎
Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, Morris Kline, p984↩︎
Dedekind本人并不同意这种表述，详情请看Morris Kline, Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, p986↩︎
Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, Morris Kline, (Chap. 41, sec. 3)↩︎
Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, Morris Kline, p987↩︎
Richard Dedekind, Essays on the Theory of Numbers↩︎
Real Numbers, Generalizations of the Reals, and Theories of Continua, Editors: Ehrlich, P. (Ed.)，page x↩︎
Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, Morris Kline, p979↩︎
Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, Morris Kline, p979↩︎
Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, Morris Kline, p982↩︎
Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, Morris Kline, p1024↩︎
Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, Morris Kline, p956↩︎
The History of the Calculus and Its Conceptual Development, Carl Benjamin Boyer, p284-286↩︎
Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, Morris Kline, p1025↩︎
Introduction to Calculus and Analysis, Volume I, Reprint of the 1989 edition, Richard Courant, Fritz John, p88↩︎
Richard Dedekind, Essays on the Theory of Numbers↩︎
笔者不懂德语，这是在谷歌翻译的辅助下阅读后的结论↩︎
Contributions to the Founding of the Theory of Transfinite Numbers, Georg Cantor; Philip E B Jourdain, p26↩︎
Richard Dedekind, Essays on the Theory of Numbers↩︎
Mathematics: The Loss of Certainty, Morris Kline, p84↩︎
Mathematics: The Loss of Certainty, Morris Kline, p88↩︎
Mathematics: The Loss of Certainty, Morris Kline, p88↩︎
Mathematics: The Loss of Certainty, Morris Kline, p95↩︎
Mathematics: The Loss of Certainty, Morris Kline, p95↩︎
Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, Morris Kline, p980↩︎
Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, Morris Kline, p1025-1026↩︎
Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, Morris Kline, p879-880↩︎
Mathematics: The Loss of Certainty, Morris Kline, p92↩︎
What Is Mathematics? Second Edition, Courant and Robbins, p54↩︎
Mathematics: The Loss of Certainty, Morris Kline, p92↩︎
Mathematics: The Loss of Certainty, Morris Kline, p97↩︎
Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, Morris Kline, p862↩︎
Mathematics: The Loss of Certainty, Morris Kline, p98↩︎
Mathematics: The Loss of Certainty, Morris Kline, p95↩︎
What Is Mathematics? Second Edition, Courant and Robbins, p54↩︎
Hans Niels Jahnke，A History of Analysis，p306↩︎
S. C. Malik， Principles of Real Analysis，P18; Editors: Ehrlich, p. (Ed.)，Real Numbers, Generalizations of the Reals, and Theories of Continua，page viii↩︎
https://www.mathsisfun.com/geometry/construct-segment3.html↩︎
What Is Mathematics? Second Edition, Courant and Robbins, p60↩︎
这种定义方法在Richard C006Furant, Fritz John, Introduction to Calculus and Analysis Volume I, Reprint of the 1989 edition, p7有提及，但书中并未发展这种方法。↩︎
Richard Dedekind, Essays on the Theory of Numbers, p5↩︎
Richard Dedekind, Essays on the Theory of Numbers, p5↩︎
Richard Dedekind, Essays on the Theory of Numbers, p9↩︎
Introduction to Calculus and Analysis, Volume I, Reprint of the 1989 edition, Richard Courant, Fritz John, p2↩︎
Real Mathematical Analysis, Charles Chapman Pugh, 1st Edition, p20↩︎
Calculus with analytic geometry, 2nd Edition, George F. Simmons, p789↩︎
David French Belding, Kevin J. Mitchell, Foundations of Analysis, 2nd Edition, p21↩︎
严格来讲从这里开始实际上有必要先介绍绝对值这个基本概念，但是通过几何的角度来理解绝对值也很简单，所以就不作介绍了。↩︎
Introduction to Calculus and Analysis, Volume I, Reprint of the 1989 edition, Richard Courant, Fritz John, p95-96↩︎
Introduction to Calculus and Analysis, Volume I, Reprint of the 1989 edition, Richard Courant, Fritz John, p97↩︎
Introduction to Calculus and Analysis, Volume I, Reprint of the 1989 edition, Richard Courant, Fritz John, p120↩︎
https://www.goteachmaths.co.uk/area-of-a-rectangle/↩︎
What Is Mathematics? Second Edition, Courant and Robbins, p399-400↩︎
Classic Set Theory: For Guided Independent Study, D.C. Goldrei, p15-16↩︎
What Is Mathematics? Second Edition, Courant and Robbins, p54↩︎
From Numbers To Analysis, Inder K Rana, p180↩︎

posted @ 2018-01-10 10:09 iMath 阅读(16919) 评论(0) 编辑收藏举报

刷新页面返回顶部