用极限（定积分）求面积的原理
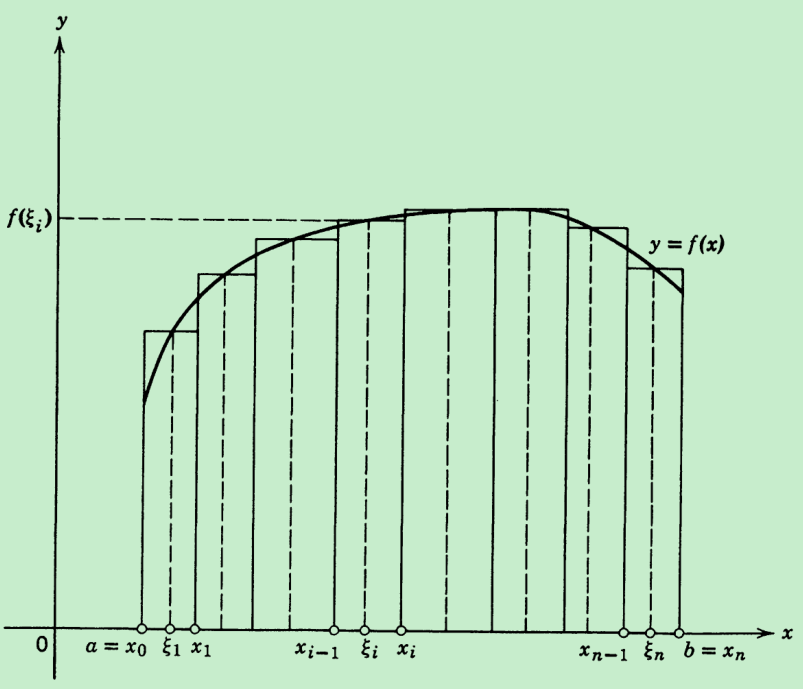如上图所示，在[a,b]上取n+1个不同的点\(x_{i}\)，即
\(a = x_{0} < x_{1} < x_{2} < \cdots < {x_{i - 1} < x}_{i} < \cdots < x_{n} = b\) （其中\(i = 1,2,\ldots,n\)）
那么[a,b]就被分成了n个小区间，其中相邻两个分点构成的闭区间\({{\lbrack x}_{i - 1},x}_{i}\rbrack\)的长度记为\(\Delta x_{i} = x_{i} - x_{i - 1}\)，因为这些点是任意取的，所以每个这种小区间的长度可以不一样，在每个小区间内任取一点\(\xi_{i}\)，用底为\(\Delta x_{i}\)，高为\(f(\xi_{i})\)（图中竖直虚线所示）的矩形近似代替对应区间内小曲边梯形的面积，这些小矩形的面积之和
\[f\left( \xi_{1} \right)\Delta x_{1} + f\left( \xi_{2} \right)\Delta x_{2} + \cdots + f\left( \xi_{n} \right)\Delta x_{n} = \sum_{i = 1}^{n}{f(\xi_{i})\Delta x_{i}}\]
就是整个大的曲边梯形面积（the area under the curve）的近似。当每个小矩形的底都越来越靠近0，即越来越窄的时候，这些小矩形的面积之和便会越来越接近大的曲边梯形的面积，
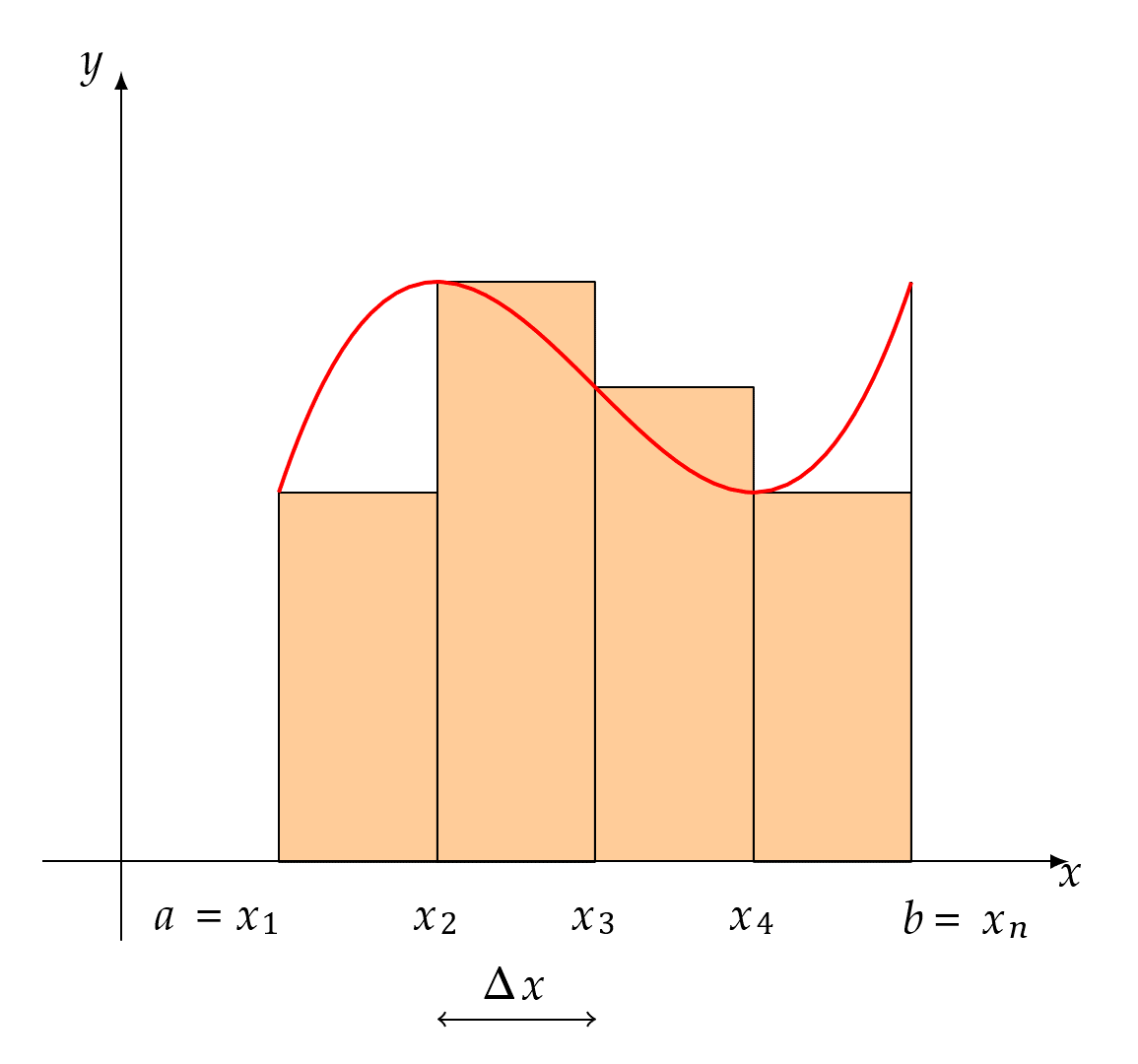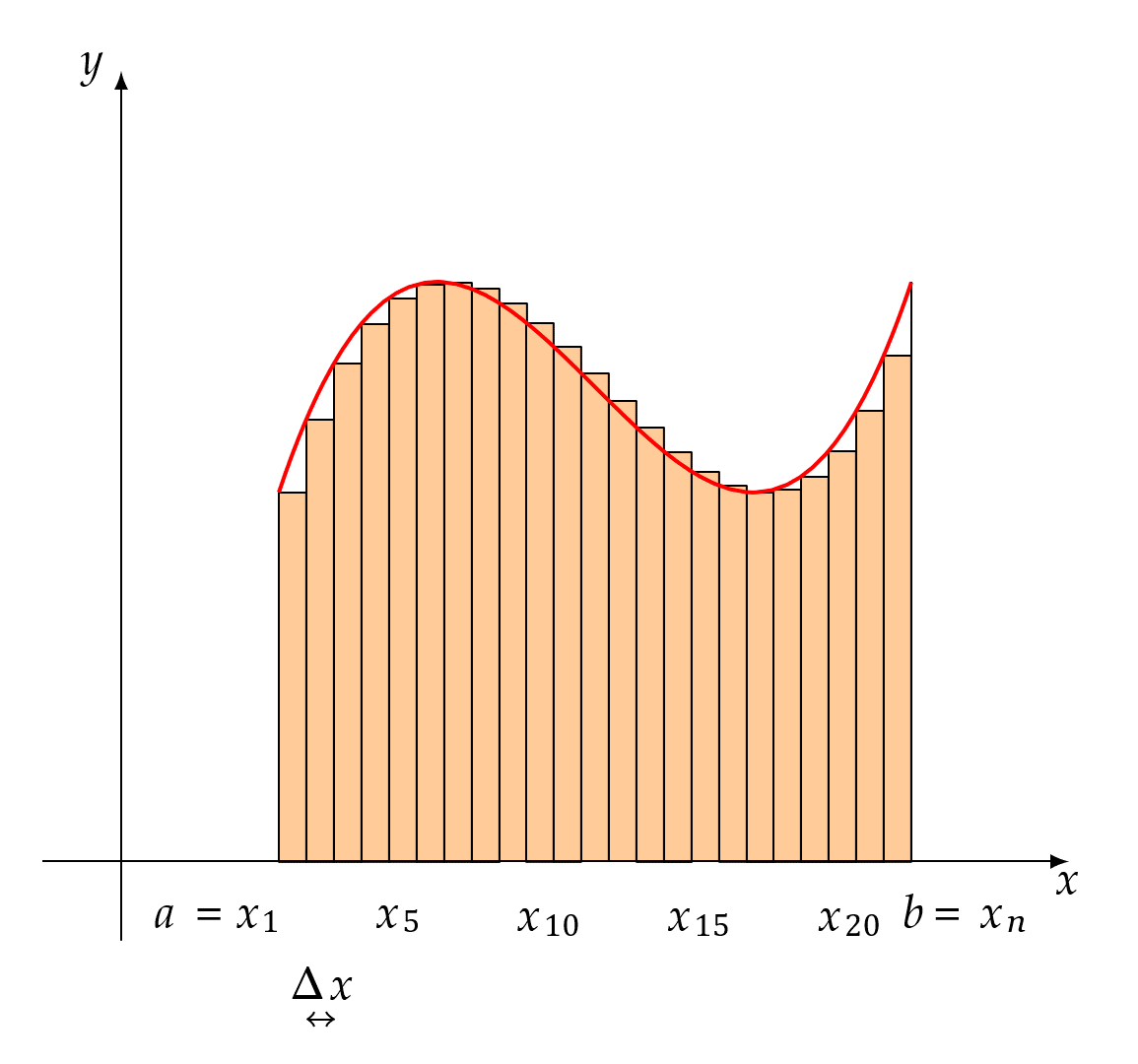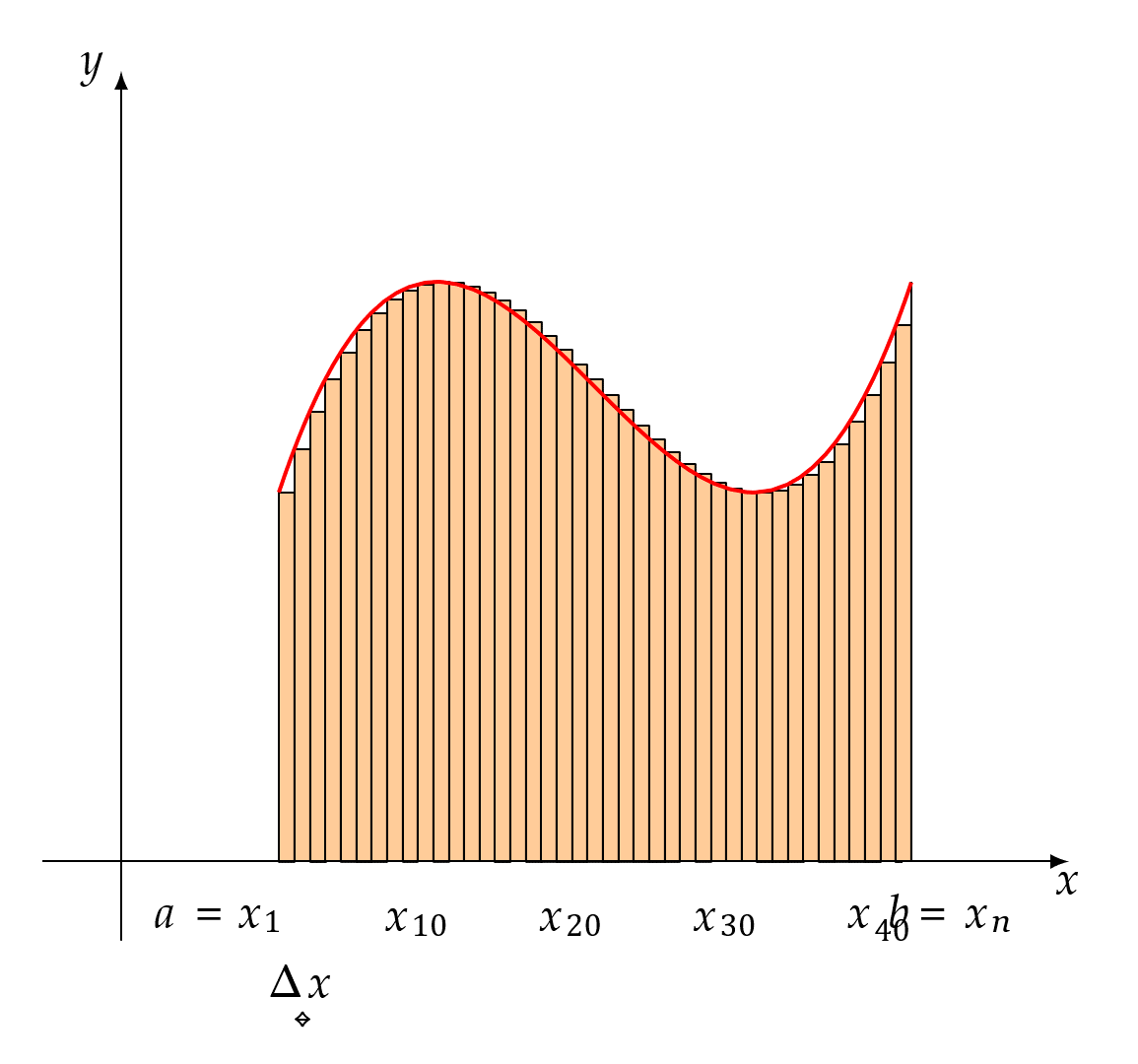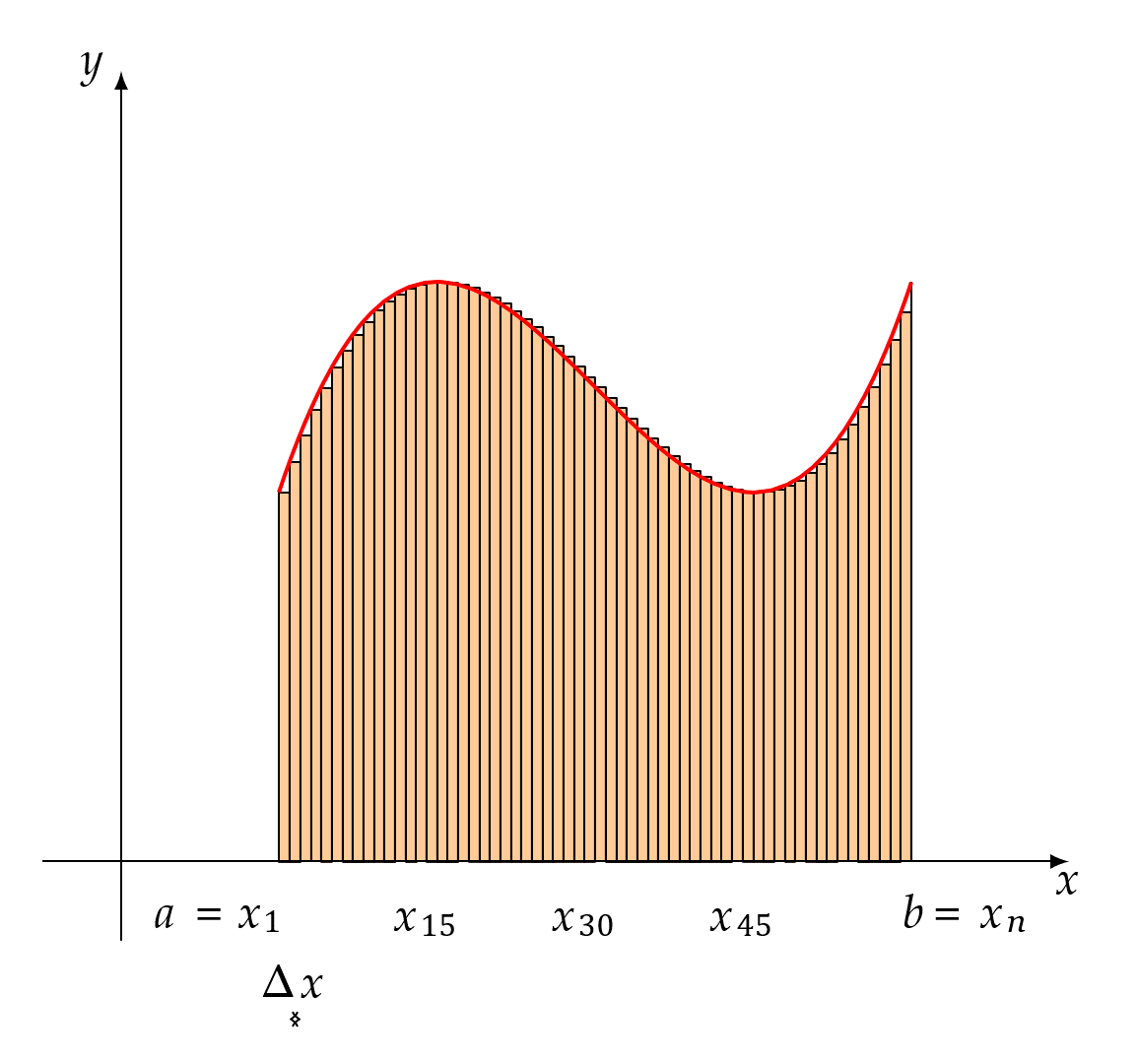
所以定这个过程中\(\sum_{i = 1}^{n}{f(\xi_{i})\Delta x_{i}}\)的极限为曲边梯形的面积就显得很自然而然了1。
“每个小矩形的底都越来越靠近0”的一种等价说法是“底边长度最大的小矩形的底越来越靠近0”（最大的都靠近0了，其余比它小的自然也更靠近0，进而每个都越来越靠近0），这种等价转述是为了方便下面用极限符号来表示上述求曲边梯形面积的原理。记底边最长的小矩形的底边长为\(\lambda\)，显然\(\lambda\)大于等于每个小矩形的底\(\Delta x_{i}\)，\(\lambda \rightarrow 0\)时，每个\(\Delta x_{i}\)也都\(\rightarrow 0\)，所以如果用S代表曲边梯形的面积的话，那么上述求面积的原理可以用数学符号表述为2
\[\begin{array}{r} \lim_{\lambda \rightarrow 0}\left( f\left( \xi_{1} \right)\Delta x_{1} + f\left( \xi_{2} \right)\Delta x_{2} + \cdots + f\left( \xi_{n} \right)\Delta x_{n} \right) = \lim_{\lambda \rightarrow 0}{\sum_{i = 1}^{n}{f\left( \xi_{i} \right)\Delta x_{i} = S}} \\ \end{array}\]
下面解答几个学习过程中可能碰到的疑点：
-
在每个小矩形的底都越来越靠近0的过程中，小矩形的总数\(n\)会越来越多（想想为什么？），即\(\lambda \rightarrow 0\)时，每个\(\Delta x_{i}\)也都\(\rightarrow 0\)，\(\ n \rightarrow \infty\)。
-
每个\(\Delta x_{i}\)都\(\rightarrow 0\)时，每个小矩形的面积\(f\left( \xi_{i} \right)\Delta x_{i} \rightarrow 0\)，而这个过程中\(n \rightarrow \infty\)，以至于有学生会认为大的曲边梯形的面积最终是无数个底为0也即面积为0的小矩形面积相加的结果，这种误解源于对极限思想的理解不到位，\(\Delta x_{i} \rightarrow 0\)意味着\(\Delta x_{i}\)在“永无止境”地越来越靠近0，所以根本不存在“\(\Delta x_{i}\)最终变成0”这么一说，同样也就不可能有\(f\left( \xi_{i} \right)\Delta x_{i}\)也变成0的说法。在极限的ε-δ定义中也明确规定过\(0 < |x - x_{0}| < \delta\)，即在\(x{\rightarrow x}_{0}\)的过程中x不会变成所趋近的点\(x_{0}\)，所以上述求面积的过程中\(\Delta x_{i}\)不会变成0。
-
既然\(\Delta x_{i}\)最终不会变成0，那么每一个小矩形和对应的小曲边梯形的面积总有差异，以至于上述极限过程中任何一个\(\sum_{i = 1}^{n}{f(\xi_{i})\Delta x_{i}}\)都不会是最终要求的曲边梯形的面积的准确值，所以面积准确值究竟是怎么求出来的呢？这同样是个对极限思想理解不到位引起的疑问，在此举一简单例子来阐明极限思想，比如“当\(x > 0\)且\(x \rightarrow 0\)时，\(x + 1 \rightarrow 1\)”，按上述说法在极限过程中\(x \neq 0\)，那么极限值1究竟是怎么计算出来的呢？当x从0的右边永无止境地越来越靠近0的时候，
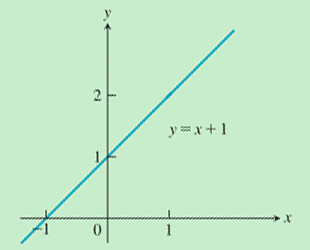
任何比1大的数终将在x不断靠近0的过程中变得大于x+1，以至于x+1最终会小于一切比1大的数，又因为\(x > 0\)，所以x+1>1，所以x+1在x无止境地越来越靠近0的过程中不会逼近任何一个比1大的数，只会逼近1，也就是说极限值1不是“等于出来的”，而是“被逼出来的”，这就是“当\(x > 0\)且\(x \rightarrow 0\)时，\(x + 1 \rightarrow 1\)”所蕴含的极限思想。同理，曲边梯形面积的准确值是通过一系列的\(\sum_{i = 1}^{n}{f(\xi_{i})\Delta x_{i}}\)在\(\lambda \rightarrow 0\)的过程中不断“逼出来的”。为了让大家彻底明白用极限求面积的原理，下面再举一例（按照上面的说法每一个小矩形的高\(f(\xi_{i})\)是可以在对应的区间内任意取的，下图就取对应小区间内最小的\(f(\xi_{i})\)），
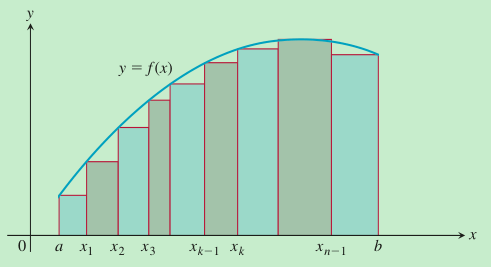
每种分割下的小矩形面积之和\(\sum_{i = 1}^{n}{f(\xi_{i})\Delta x_{i}}\)都比要求的曲边梯形的面积要小，但是在每个小矩形的底都越来越靠近0的过程中，\(\sum_{i = 1}^{n}{f(\xi_{i})\Delta x_{i}}\)终将超越任何一个比面积准确值小的值，从而把面积准确值给逼出来。
有学生可能会说：“好吧，我承认\(\Delta x_{i}\)最终不会变成0，但它最终会变成一个比0大并且比任何正实数都小的‘无穷小量’，那么\(f\left( \xi_{i} \right)\Delta x_{i}\)也会变成无穷小量，所以大的曲边梯形的面积最终是无数个无穷小量的和”，这种误解从18世纪就有了。首先这种说法提到了\(\Delta x_{i}\)“最终”会变成无穷小量，同样是认为极限过程有一个最终状态，犯了上面2中说到的错误，仅这一点就可以否定这种理解；其次在于错误地认为存在“一个比0大并且比任何正实数都小的无穷小量”，要纠正这种错误观念首先应该认识到我们讨论的用极限求面积是在什么数系范围内进行的——实数系，而根据实数系内的阿基米德性质（Archimedean Property for Real Numbers）：对于任意正实数x，总存在正整数n使得\(\frac{1}{n} < x\)，所以在实数系内不存在“一个比0大并且比任何正实数都小的无穷小量”，因为总有比该量还小的\(\frac{1}{n}\)存在。这种误解在Introduction to Calculus and Analysis Volume I, Reprint of the 1989 edition, Richard Courant, Fritz John, p125处也说过：The definition of the integral as the limit of a sum led Leibnitz to express the integral by the following symbol:
\[\int_{a}^{b}\mspace{2mu} f(x)dx\]
The integral sign is a modification of the summation sign in the shape of a long \(S\)used at Leibnitz's time. The passage to the limit from a finite subdivision into portions \(\Delta x_{i}\)is indicated by the use of the letter \(d\)in place of \(\Delta.\) In using this notation, however, we must not tolerate the eighteenth century mysticism of considering \(dx\) as an "infinitely small" or "infinitesimal quantity," or considering the integral as a "sum of an infinite number of infinitely small quantities." Such a conception is devoid of clear meaning and obscures what we have previously formulated with precision. From our present viewpoint the individual symbol \(dx\) has not been defined at all. The suggestive combination of symbols \(\int_{a}^{b}\mspace{2mu} f(x)dx\)is defined for a function \(f(x)\) in the interval \(\lbrack a,b\rbrack\) by forming the ordinary sums \(F_{n}\) and passing to the limit as \(n \rightarrow \infty\).
上述取多个小矩形面积之和的极限来计算曲边梯形面积的方法显然也适用于计算下图中由y=2x、x=1、x=5及其x轴围成的梯形的面积，
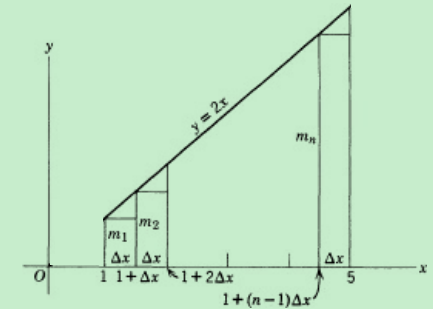
而我也打算用这个例子来说明用极限求面积得出来的结果是准确的3。
首先将[1,5]等分成n个小区间，则每个小矩形的底长\(\Delta x = \frac{5 - 1}{n} = \frac{4}{n}\)，取每个小区间左端点对应的函数值为对应小区间内的小矩形的高，则所有小矩形的面积之和\(\begin{matrix} S_{n} & = 2\Delta x + 2(1 + \Delta x)\Delta x + 2(1 + 2\Delta x)\Delta x + \cdots + 2\lbrack 1 + (n - 1)\Delta x\rbrack\Delta x \\ & = 2\Delta x \cdot \frac{\lbrack 2 + (n - 1)\Delta x\rbrack \cdot n}{2} \\ & = n\Delta x\lbrack 2 + (n - 1)\Delta x\rbrack \\ & = 24 - \frac{16}{n} \\ \end{matrix}\)
当每个小矩形的底\(\Delta x\)都越来越靠近0，即\(\Delta x \rightarrow 0\)，这些小矩形的面积之和便会越来越接近大的梯形的面积，因为\(\Delta x = \frac{4}{n}\)，所以这里\(\Delta x \rightarrow 0\)等同于\(n \rightarrow \infty\)，因此定\(\lim_{n \rightarrow \infty}\left( 24 - \frac{16}{n} \right) = 24\)为梯形的面积就显得很自然而然了，而这个极限值和我们用梯形面积公式求出来的结果\(\frac{(2 + 10) \bullet 4}{2} = 24\)是一样的，这说明了通过极限求出来的面积值是准确的，也印证了上面所说：在极限过程中的任何一个\(S_{n} = 24 - \frac{16}{n}\)都不会是最终要求的面积的准确值，其值是通过极限过程由一系列的\(S_{n}\)“给逼出来的”。
