CF50C Happy Farm 5 题解

这题真是把我恶心到了。

建议在看此题解之前读一下 这篇题解

看完感觉是几乎没懂，只理解了 \(+4\) 的意思

先贴一下代码

#include <cstdio>
#include <algorithm>
#define inf 0x3f3f3f3f
using namespace std;
int main(){
	int n,a,b,c,d;
	a=b=-inf;c=d=inf;
	scanf("%d",&n);
	for(int i=1,x,y;i<=n;++i){
		scanf("%d%d",&x,&y);
		a=max(x+y,a);
		b=max(x-y,b);
		c=min(x+y,c);
		d=min(x-y,d);
	}
	printf("%d",a+b-c-d+4);
	return 0;
}

我将会用画图的方法解释该代码：

容易证明画一条覆盖或者包含所有点的线 \(+4\) 即可得到正确结果。

因为斜着走和直着走的花费是一样的，所以在能斜着走的时候就尽量斜的走，相当于给你了一份花费获得了两倍的收获。

由此可发现走菱形是最优的，也就是只走与平面直角坐标系中平分一三象限的直线或平分二四象限的直线平行的线。

这里通过解释样例来解释：

显然，底下的图片不符合刚刚分析的规则。

所以，将所有与 \(x,y\) 轴平行的直线全部替换为斜线。

如图所示：

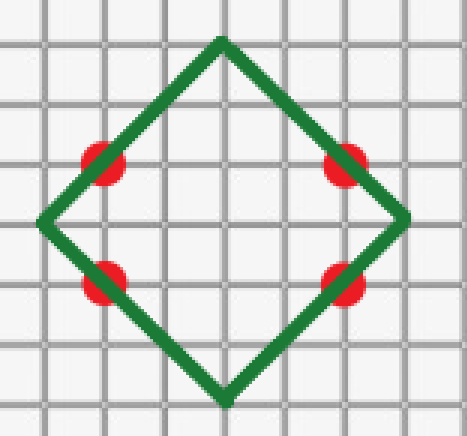
统计一下答案：\(3 \times 4 + 4 = 16\)

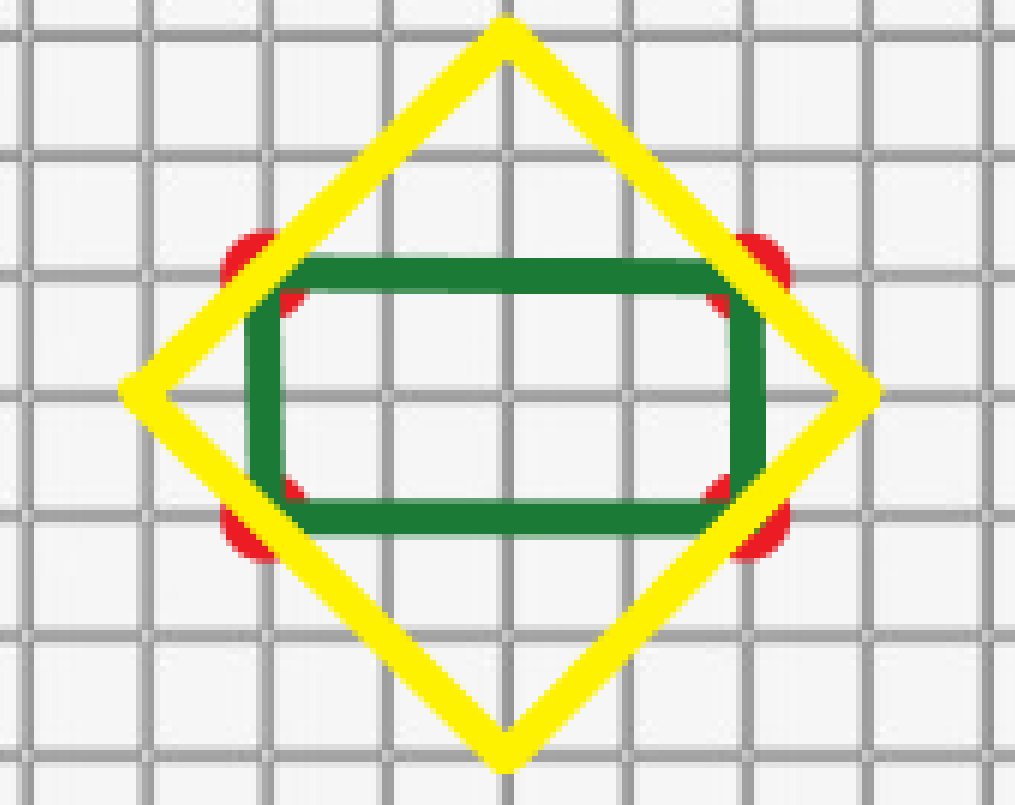
根据代码，总共分为四部解释，其中红色线代表被删除，黄色线代表被添加：

一下都是根据 a+b-c-d+4 理解

第一步：根据 a=max(x+y,a);

根据输入，判断出 \(x+y\) 值最大的点为右上角的点：

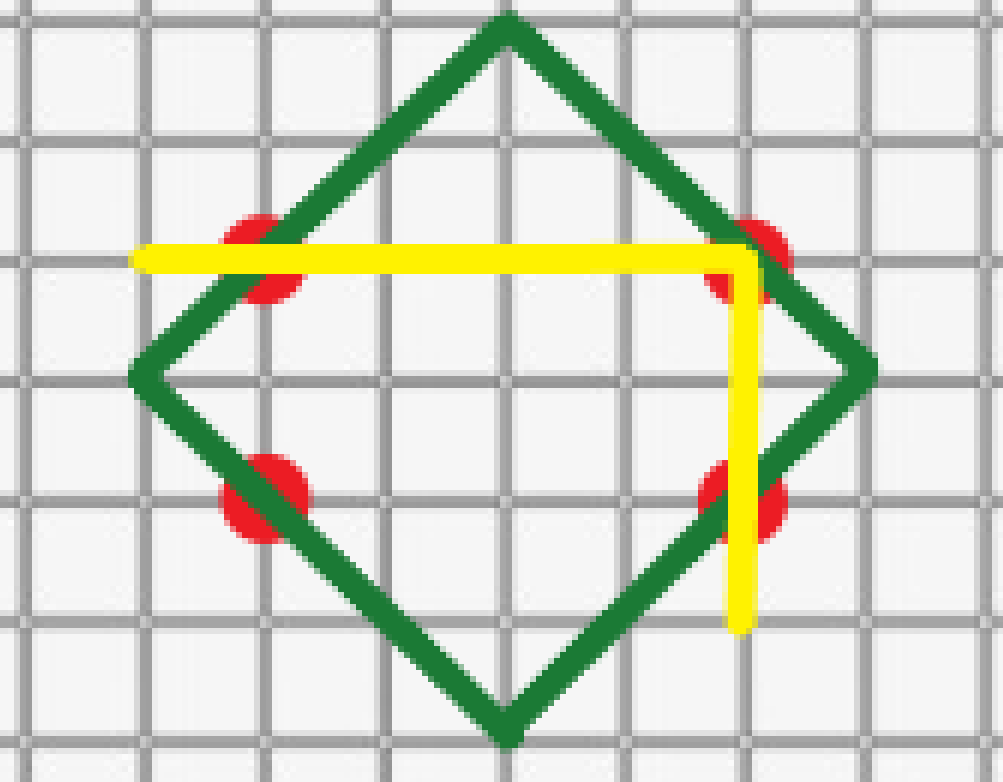
随后将他平移至菱形里面：

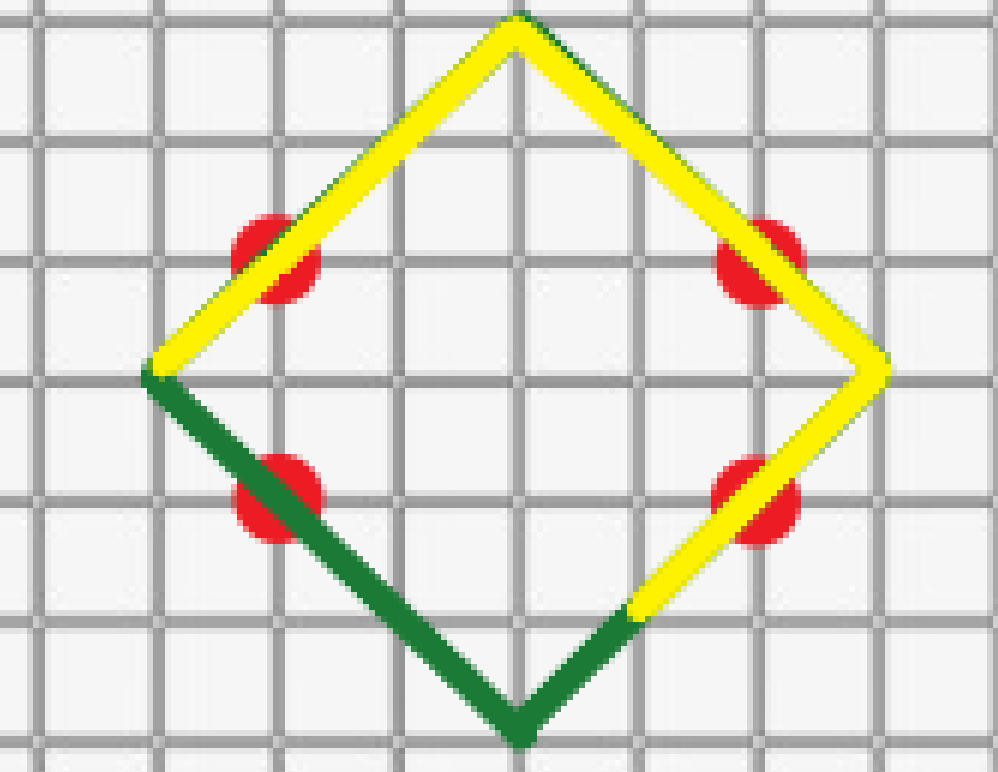
第二步：根据 b=max(x-y,b);

根据输入，判断出 \(x-y\) 的值最大的点为右下角的点：

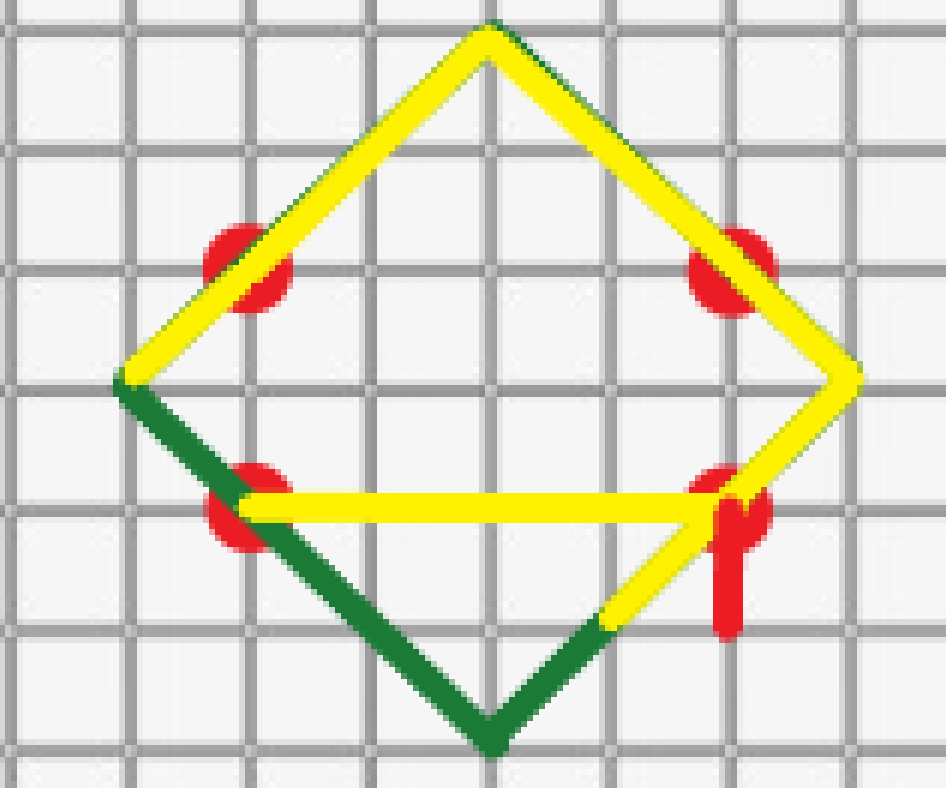
随后将红色的一小段和黄色的一小段抵消，剩下的黄色移入菱形：

第三步：根据 c=min(x+y,c);

根据输入，判断出 \(x+y\) 的值最小值的点为左下角的点：

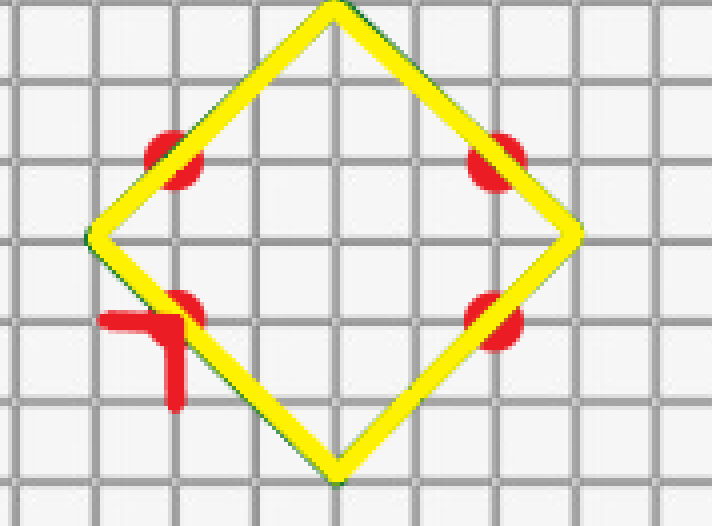
将红色的小段与黄色的小段抵消，得到：

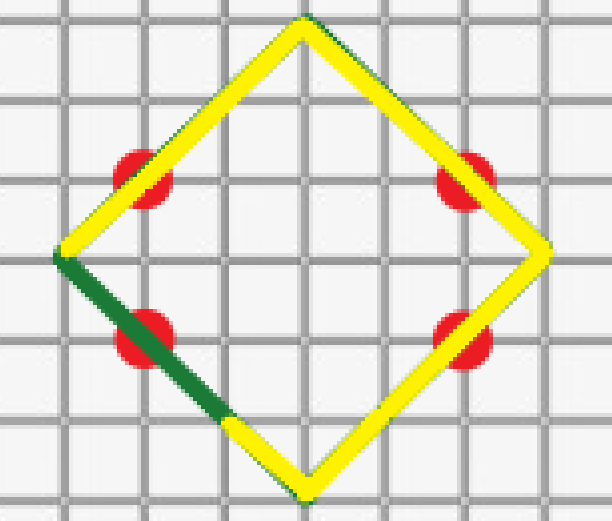
第四步：根据 d=min(x-y,d);

根据输入，判断出 \(x-y\) 的值最小值的点为左上角的点：

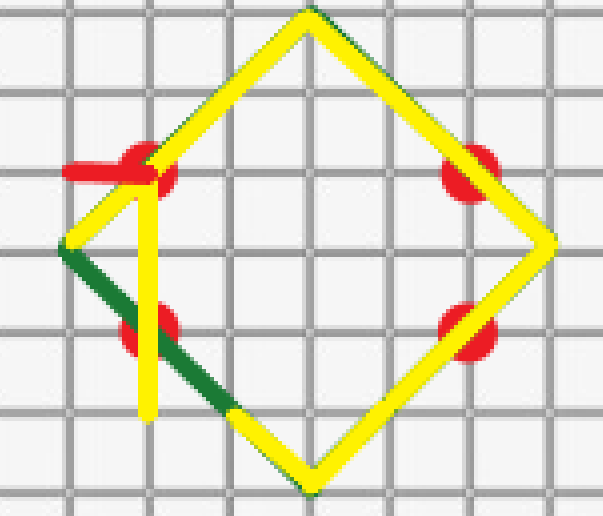
将红色小段与黄色小段抵消，剩下的移入菱形，得到：

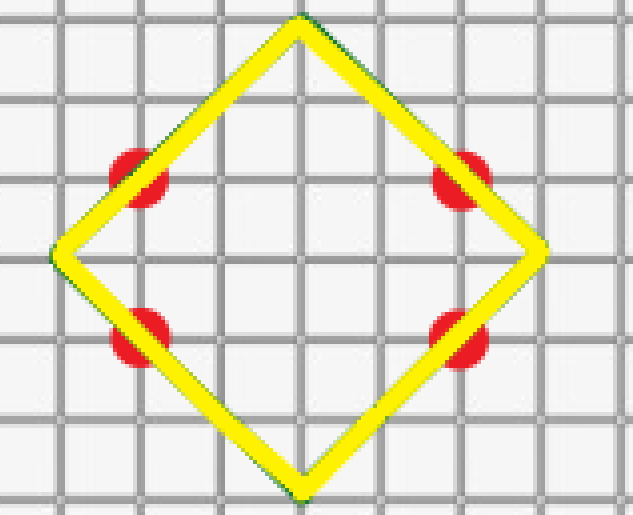
至此，菱形全部被黄色段覆盖，且没有多余，解释完毕。

当然以这种方法，它的正确性可以被证明。

最优性：