有关容斥的知识及题目解析

小目录：

一，容斥原理

二，子集反演

三，最值反演（$\textit{Min_Max}$容斥）

四，斯特林反演

五，单位根反演

由于是学习Lrefrain学长的笔记，所以大量资源摘自学长博客

以及以下很多柿子的证明在学长的博客里面也可以找到。

---

前置概念

一，第一类斯特林数：

$\begin{bmatrix}n\\k\end{bmatrix}$

那个大的中括号叫做 轮换 ，意思是将$n$个元素划分成$k$集合，每个集合进行 圆排列 的方案数。

圆排列：将长度为$n$的序列连成一个环，不同的排列数。其实就是$P_n=(n-1)!$，这里P是圆排列

关于其有一个递推式

$\begin{bmatrix}n\\k\end{bmatrix}=\begin{bmatrix} n-1\\k-1 \end{bmatrix}+(n-1)\begin{bmatrix}n-1\\k\end{bmatrix}$

证明可以类似用组合数的方法，原来有$n-1$个元素，划分了$k-1$个集合的方案加上一个新加的集合贡献的方案。

有三个性质：

一，

$\sum_{i=0}^{n} \begin{bmatrix}n\\i\end{bmatrix}=n!$

写两种不同的排列，然后映射连边，组成环的个数就是划分集合的个数，然后依次类推，组成一个环的排列，两个环的排列。。。。

 

 

 

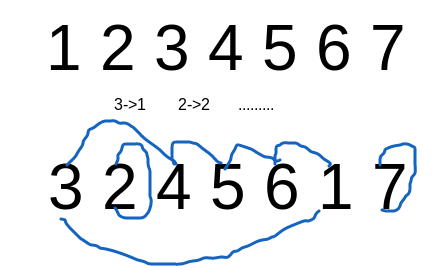
 如图就是$\begin{bmatrix}7\\3\end{bmatrix}$的图示了，其他的加和推广可以yy，比较好想。

二，

$x^{\underline{n}}=\sum_{i=0}^{n}(-1)^{n-i}\begin{bmatrix}n\\i\end{bmatrix}x^i$

此柿子可以用归纳法证明。

其中$\underline{n}$是表示降幂，同理$\overline{n}$表示升幂

三，

$x^{\overline{n}}=\sum_{i=0}^{n}\begin{bmatrix}n\\i\end{bmatrix}x^i$

同样的，这里就不证明了。

这几条性质可以解决升幂变化通幂再变化升幂或者降幂等等的转化，比较好用

有其是组合数里面的那种降幂。

二，第二类斯特林数：

$\begin{Bmatrix}n\\k\end{Bmatrix}$

表示$n$个元素划分为$k$个集合的方案数。

比上一个好理解。。。。

通项公式：

$\begin{Bmatrix}n\\m\end{Bmatrix}=\sum_{i=0}^{m}\frac{(-1)^{m-i}i^n}{i!(m-i)!}$

递推式：

$\begin{Bmatrix}n\\k\end{Bmatrix}=\begin{Bmatrix}n-1\\k-1\end{Bmatrix}+k\begin{Bmatrix}n-1\\k\end{Bmatrix}$

同样有几个性质。

一，

$k^n=\sum_{i=0}^{k}\begin{Bmatrix}n\\i\end{Bmatrix}i!\binom{k}{i}=\sum_{i=0}^{k}\begin{Bmatrix}n\\i\end{Bmatrix}k^{\underline{i}}$

我们在$k$个集合中选择$i$个集合放入元素然后全排列这些集合（因为没有标号），得到的就是$n$个元素放入$k$个可空集合的方案数

 

 二，

$\begin{Bmatrix}n\\k\end{Bmatrix}=\frac{1}{k!}\sum_{i=0}^{k}(-1)^i\binom{k}{i}(k-i)^n$

$\begin{Bmatrix}n\\k\end{Bmatrix}=\sum_{i=0}^{k}(-1)^i\frac{1}{i!}\frac{(k-i)^n}{(k-i)!}$

 上面的柿子化简可得下式。(下面的那个类似通项公式，好像直接记住通项就行)

---

前置知识完毕，$L_AT^EX$显然已经打废了。。。。

 一，容斥原理：

$\left | \bigcup_{i=1}^{n} S_i\right |=\sum_{C\subseteq M}^{n}(-1)^{size(C)-1}\left | \bigcap_{T \subseteq C}^{} T\right |$

比较好理解，就是小学奥数的那种三个圆套在一起，什么加一次减两次得到个面积，就是这个公式的通俗化变形。

证明用二项式定理$(1-1)^n$具体详见学长博客。

 

二，子集反演：

$g(S)=\sum_{T \subseteq S}f(T)$

$f(S)=\sum_{T \subseteq S}(-1)^{|S|-|T|}g(T)$

证明比较简单，奇加偶减就可以理解。

 

三，最值反演（$\textit{Min_Max}$容斥）：

$Max(S)=\sum_{\phi  \neq  T \subseteq S}(-1)^{|T|-1}Min(T)$

其中$Max(S)$是集合$S$中最大的元素，后面的$Min(T)$同理。上式在那个最值函数外面套一个期望函数也成立。

这类柿子在后面的题中会用到。

 

四，斯特林反演：

$f(n)=\sum_{i=0}^{n}\begin{Bmatrix}n\\i\end{Bmatrix}g(i)\Leftrightarrow g(n)=\sum_{i=0}^{n}\begin{bmatrix}n\\i\end{bmatrix}(-1)^{n-i}f(i)$

有点类似二项式反演的柿子，比较好记。

然后这里证明这个柿子用到两个引理，只写下公式：

$x^{\underline n}=(-1)^n(-x)^{\overline n}$

$x^{\overline n}=(-1)^n(-x)^{\underline n}$

具体证明只需将升幂/降幂的拆开消项就行。

两个反转公式：

$\sum_{i=m}^{n}(-1)^{n-i}\begin{bmatrix}n\\i\end{bmatrix}\begin{Bmatrix}i\\m\end{Bmatrix}=[m=n]$

$\sum_{i=m}^{n}(-1)^{n-i}\begin{Bmatrix}n\\i\end{Bmatrix}\begin{bmatrix}i\\m\end{bmatrix}=[m=n]$

这些东西只是在证明斯特林反演时会用到。。。。。。

还有一种至少形式：

$f(m)=\sum_{i=m}^{n}\begin{Bmatrix}i\\m\end{Bmatrix}g(i)\Leftrightarrow g(m)=\sum_{i=m}^{n}\begin{bmatrix}i\\m\end{bmatrix}(-1)^{i-m}f(i)$

同样很像二项式定理，比较好记。

 

五，单位根反演：

$[k|n]=\frac{1}{k}\sum_{i=0}^{k-1}w^{i*n}_{k}$

证明：

如果$k|n$，那么$w^{n}_{k}=1$

所以：

$\frac{1}{k}\sum_{i=0}^{k-1}w^{0}_{k}=[k|n]=1$

如果$k$不整除于$n$，那么$w^{n}_{k}\neq1$，可以用等比数列求和公式

$0=[k|n]=\frac{1}{k}w^{0}_{k}\frac{1-w^{n*k}_{k}}{1-w^{n}_{k}}=0$

关于知识类型的就这么多了，下面是例题，也是唯一一个切出来的题。

---

 

 

随机游走

比较$diao$的一道题。

由于上面说过$\textit{Min_Max}$容斥外面套一个期望函数也可以用，那么这题我们也考虑使用最值反演。

可知，此题的$Min$表示集合中最先到达的点的期望时间，$Max$表示最后到达的点的期望时间，就是答案。

那么我们只要求出$Min$，就可一求出$Max$。

我们设$dp_x$表示对于一个集合$S$，从$x$第一次到达$S$的期望时间

$d_x$为$x$的度数。

可以得到转移方程：

$dp_x= \left\{\begin{matrix}0 &x\in S \\ \frac{dp_{fa}+1}{d_x}+\frac{\sum_{c \in son_x}(dp_c+1)}{d_x} & x\notin S\end{matrix}\right.$

一种解法是列出$n$个方程，高斯消元求解。最后$Min(S)=dp_{st}$

然后$FWT$卷积。但是时间复杂度不允许。。。。。

考虑使用原来Lrefrain学长讲的系数递推优化。重点是优化$x \notin S$的部分

$dp_x=\frac{dp_{fa}+1}{d_x}+\frac{\sum_{c \in son_x}(dp_c+1)}{d_x}
=\frac{dp_{fa}}{d_x}+\frac{\sum_{c \in son_x}dp_c}{d_x}+\frac{1}{d_x}+\frac{num_{son_x}}{d_x}=\frac{dp_{fa}}{d_x}+\frac{\sum_{c \in son_x}}{d_x}+1
=A_x*dp_{fa}+B_x$

然后用设的这个$A_x,B_x$来替换$dp_c$，然后移项，拆开$sigma$。。。

$dp_x=\frac{dp_{fa}}{d_x}+\frac{\sum_{c \in son_x}}{d_x}+1
=\frac{dp_{fa}}{d_x}+\frac{\sum_{c \in son_x}(A_c*dp_x+B_c)}{d_x}+1
$

$dp_x=\frac{dp_{fa}}{d_x}+\frac{\sum_{c \in son_x}(A_c*dp_x+B_c)}{d_x}+1$

$dp_x*d_x=dp_{fa}+\sum_{c \in son_x}(A_c*dp_x+B_c)+d_x=dp_{fa}+dp_x*\sum_{c \in son_x}A_c+\sum_{c \in son_x}B_c+d_x$

$dp_x*(d_x-\sum_{c \in son_x}A_c)=dp_{fa}+\sum_{c \in son_x}B_c+d_x$

$dp_x=\frac{1}{d_x-\sum_{c \in son_x}A_c}dp_{fa}+\frac{\sum_{c \in son_x}B_c+d_x}{d_x-\sum_{c \in son_x}A_c}$

$\begin{cases}A_x=\frac{1}{d_x-\sum_{c \in son_x}A_c}\\ B_x=\frac{\sum_{c \in son_x}B_c+d_x}{d_x-\sum_{c \in son_x}A_c}\end{cases}.$

然后直接树形$dp$求解出$A_x,B_x$。（其实是用待定系数法得到的解），然后就可以求出$Min$了，最后使用$FWT$卷积求解$Max$即可。

 关于$FWT$卷积，可以用高维前缀和理解。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int NN=(1<<20),MM=20,p=998244353;
int n,Q,rt,deg[MM],ret[NN],A[MM],B[MM];
struct SNOW{int to,next;};SNOW e[MM<<1];int head[MM],rp;
inline void add(int x,int y){
    e[++rp]=(SNOW){y,head[x]}; head[x]=rp;
    e[++rp]=(SNOW){x,head[y]}; head[y]=rp;
}
inline int qmo(int x){
    int ans=1,b=p-2,c=p; x%=c;
    while(b){
        if(b&1) ans=(ans*x)%c;
        b>>=1; x=(x*x)%c;
    }return ans;
}
inline void dfs(int fa,int x,int S){
    if(S>>(x-1)&1) return;
    int sumA=0,sumB=0;
    for(int i=head[x];i;i=e[i].next){
        int y=e[i].to;if(y==fa) continue;
        dfs(x,y,S);
        (sumA+=A[y])%=p;
        (sumB+=B[y])%=p;
    }int inv=qmo((deg[x]-sumA+p)%p);
    A[x]=inv; B[x]=inv*(deg[x]+sumB)%p;
}
inline void FWTor(int s[],int n){
    for(int i=2;i<=n;i<<=1)
        for(int j=0;j<n;j+=i)
            for(int k=0;k<(i>>1);k++)
                (s[(i>>1)+j+k]+=s[j+k])%=p;
}
namespace WSN{
    inline short main(){
        scanf("%lld%lld%lld",&n,&Q,&rt);
        for(int i=1,u,v;i<n;i++)
            scanf("%lld%lld",&u,&v),add(u,v),++deg[u],++deg[v];
        for(int i=0;i<(1<<n);i++){
            memset(A,0,sizeof(A)); memset(B,0,sizeof(B));
            dfs(0,rt,i); int cnt=__builtin_popcount(i);
            ret[i]=((cnt&1)? B[rt]:(p-B[rt])%p);
        }
        FWTor(ret,(1<<n));
        while(Q--){
            int x,m,sta=0;scanf("%lld",&m);
            for(int i=1;i<=m;i++) scanf("%lld",&x),sta|=(1<<(x-1));
            printf("%lld\n",ret[sta]);
        }
        return 0;
    }
}
signed main(){return WSN::main();}

最后的最后，粘贴一下博客后台的不容易，希望求个推荐（~^v^~）。