Noip模拟11 2021.7.11
T1 math
其实看看题面，看看给的那机组数据即可看出规律了（然而当时并没有，只是发现模数的循环节，存了个vector，接下来就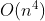
暴力了）
有个柿子: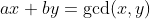 
其实就是裴蜀定理。
然后想一想的话就是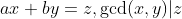
那么只要求出Ν个的gcd再和k求gcd，算出来之后用这个总的gcd去进行翻倍
反到最大的小于k的数停止即可
1 #include<bits/stdc++.h> 2 #define int long long 3 #define write(X) printf("%lld\n",X) 4 #define Min(A,B) ((A)<(B)?(A):(B)) 5 using namespace std; 6 inline int read(){ 7 int x=0,f=1; char ch=getchar(); 8 while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); } 9 while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } 10 return x*f; 11 } 12 const int NN=5e6; 13 int n,k,GCD,ans[NN],tot; 14 inline int gcd(int a,int b){ 15 if(b==0) return a; 16 return gcd(b,a%b); 17 } 18 namespace WSN{ 19 inline int main(){ 20 n=read(),k=read(); 21 GCD=gcd(read(),k); 22 for(int i=1;i<n;i++){ int a=read();GCD=gcd(GCD,a);} 23 // cout<<GCD<<endl; 24 for(int i=0;i<=k;i++){ 25 if(GCD*i>=k) break; 26 ans[++tot]=GCD*i; 27 } 28 write(tot); 29 for(int i=1;i<=tot;i++) printf("%lld ",ans[i]); 30 return 0; 31 } 32 } 33 signed main(){return WSN::main();} 34 // FILE *A=freopen(".in","r",stdin); 35 // FILE *B=freopen("aaa.out","w",stdout);
T2 biology
这题当时一看是个dp就先去看T3了，T3水了个线段树回来干打了一个正确性颇高的贪心
正解的初始柿子还是很好想的，不过对于dp弱者来说循环就很麻烦。。。
可是，这题的循环也并不麻烦。。。
首先柿子：
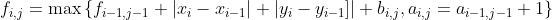
然后看上届大佬的题解里说道：
dp方程里面的绝对值要拆开！！！
然后可以得到四种不同的情况：
将绝对值拆开,四个二维树状数组分别维护最大值：
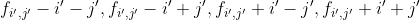
可以画图，将一个方块分成四块，田字格中点为（i，j），则从左上，左下，右上，右下的四个区域v向此处转移，按照绝对值划分可分为：
然后进行转移即可：
1 #include<bits/stdc++.h> 2 #define int long long 3 #define write(X) printf("%lld\n",X) 4 #define Max(A,B) ((A)>(B)?(A):(B)) 5 using namespace std; 6 inline int read(){ 7 int x=0,f=1; char ch=getchar(); 8 while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); } 9 while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } 10 return x*f; 11 } 12 const int NN=2005,MM=2005*2005,NM=1e6+5; 13 int n,m,a[NN][NN],b[NN][NN],cnt; 14 int f[NN][NN]; 15 vector< pair< int,int > > vc[MM]; 16 bool vis[MM]; 17 struct SNOW{ 18 int t[NN][NN]; 19 inline int lobit(int x){return x&(-x);} 20 inline void update(int x,int y,int val){ 21 for(int i=x;i<=n;i+=lobit(x)) for(int j=y;j<=m;j+=lobit(y)) t[i][j]=Max(t[i][j],val); 22 } 23 inline int query(int x,int y){ 24 int ans=0; 25 for(int i=x;i;i-=lobit(x)) for(int j=y;j;j-=lobit(y)) ans=Max(ans,t[i][j]); 26 return ans; 27 } 28 }t1,t2,t3,t4; 29 int na[MM],rk[MM]; 30 inline bool cmp(int a,int b){return a<b;} 31 namespace WSN{ 32 inline int main(){ 33 n=read(),m=read(); 34 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){ 35 a[i][j]=read(); 36 if(!vis[a[i][j]] && a[i][j]) vis[a[i][j]]=1,na[++cnt]=a[i][j]; 37 } 38 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) b[i][j]=read(); 39 sort(na+1,na+cnt+1,cmp); 40 for(int i=1;i<=cnt;i++) rk[na[i]]=i; 41 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) 42 if(a[i][j]) vc[rk[a[i][j]]].push_back(make_pair(i,j)); 43 for(int i=0;i<vc[1].size();i++){ 44 int x=vc[1][i].first,y=vc[1][i].second,vb=b[x][y]; 45 t1.update(x,y,vb-x-y);t2.update(x,m-y+1,vb-x+y);t3.update(n-x+1,y,vb+x-y);t4.update(n-x+1,m-y+1,vb+x+y); 46 } 47 for(int i=2;i<=cnt;i++){ 48 for(int j=0;j<vc[i].size();j++){ 49 int x=vc[i][j].first,y=vc[i][j].second,vb=b[x][y]; 50 f[x][y]+=Max(t1.query(x,y)+x+y+vb,Max(t2.query(x,m-y+1)+x-y+vb,Max(t3.query(n-x+1,y)-x+y+vb,t4.query(n-x+1,m-y+1)-x-y+vb))); 51 } 52 for(int j=0;j<vc[i].size();j++){ 53 int x=vc[i][j].first,y=vc[i][j].second,v=f[x][y]; 54 t1.update(x,y,v-x-y);t2.update(x,m-y+1,v-x+y);t3.update(n-x+1,y,v+x-y);t4.update(n-x+1,m-y+1,v+x+y); 55 } 56 } 57 int jie=0; 58 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) jie=Max(jie,f[i][j]); 59 write(jie); 60 return 0; 61 } 62 } 63 signed main(){return WSN::main();}
然而这只是四十分的打法....
正解其实不用考虑各种合法状态，因为最优状态是唯一的，绝对值对于你转移的方向是有限制的（即对于其他不合法状态，也就是绝对值出现负数的情况一定没有出现正数优）。那么先将节点转移为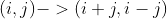
，便可以只记录四个变量
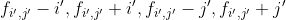，找出最大的一步合法状态即可。
1 #include<bits/stdc++.h> 2 #define int long long 3 #define write(X) printf("%lld\n",X) 4 #define Max(A,B) ((A)>(B)?(A):(B)) 5 using namespace std; 6 inline int read(){ 7 int x=0,f=1; char ch=getchar(); 8 while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); } 9 while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } 10 return x*f; 11 } 12 const int NN=2005,MM=2005*2005,NM=1e6+5; 13 int n,m,a[NN][NN],b[NN][NN],cnt; 14 int f[NN][NN]; 15 vector< pair< int,int > > vc[MM]; 16 bool vis[MM]; 17 int t1,t2,t3,t4; 18 int na[MM],rk[MM]; 19 inline bool cmp(int a,int b){return a<b;} 20 namespace WSN{ 21 inline int main(){ 22 n=read(),m=read(); 23 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){ 24 a[i][j]=read(); 25 if(!vis[a[i][j]] && a[i][j]) 26 vis[a[i][j]]=1,na[++cnt]=a[i][j]; 27 } 28 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) b[i][j]=read(); 29 sort(na+1,na+cnt+1,cmp); 30 for(int i=1;i<=cnt;i++) rk[na[i]]=i; 31 for(int i=1;i<=n;i++) 32 for(int j=1;j<=m;j++) 33 if(a[i][j]) vc[rk[a[i][j]]].push_back(make_pair(i+j,i-j)); 34 for(int i=0;i<vc[1].size();i++){ 35 int x=vc[1][i].first,y=vc[1][i].second,opx=x+y>>1,opy=x-y>>1,vb=b[opx][opy]; 36 t1=Max(t1,vb-x); t2=Max(t2,vb+x); t3=Max(t3,vb-y); t4=Max(t4,vb+y); 37 } 38 for(int i=2;i<=cnt;i++){ 39 for(int j=0;j<vc[i].size();j++){ 40 int x=vc[i][j].first,y=vc[i][j].second,opx=x+y>>1,opy=x-y>>1,vb=b[opx][opy]; 41 int ans1=t1+vb+opx+opy,ans2=t2+vb-opx-opy,ans3=t3+vb+opx-opy,ans4=t4+vb-opx+opy; 42 int ans=Max(ans1,Max(ans2,Max(ans3,ans4))); 43 f[opx][opy]+=ans; 44 } 45 for(int j=0;j<vc[i].size();j++){ 46 int x=vc[i][j].first,y=vc[i][j].second,opx=x+y>>1,opy=x-y>>1,v=f[opx][opy]; 47 t1=Max(t1,v-x); t2=Max(t2,v+x); t3=Max(t3,v-y); t4=Max(t4,v+y); 48 } 49 } 50 int jie=0; 51 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) 52 jie=Max(jie,f[i][j]); 53 write(jie); 54 return 0; 55 } 56 } 57 signed main(){return WSN::main();}
T3 english
这个题首先一看小的点线段树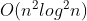
可过，不过大的点就很吓人。。。。
所以，对于预处理，应该处理出
表示序列第i个数之前（包括他）的第j位一共有多少个1
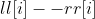表示a[i]是区间内最大值的左端点和右端点。
那么对于opt==1的情况，运用单调栈扫一边即可。还要注意疑惑对a[k]的贡献，有一个柿子：
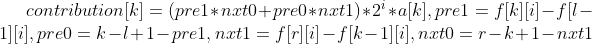
k,l,r分别表示循环到的序列第k位，以其为最大值的左/右端点。i表示二进制位数。
然后就是opt==2。。。。
这是个可持久化trie树，还没学，于是花了一下午和一晚上学习了主席树和可持久化trie。。。太男了
trie树在查找的时候也是维护了一个类似前缀和的东西。
1 #include<bits/stdc++.h> 2 #define int long long 3 #define write(X) printf("%lld\n",X) 4 #define Min(A,B) ((A)<(B)?(A):(B)) 5 #define Max(A,B) ((A)>(B)?(A):(B)) 6 using namespace std; 7 inline int read(){ 8 int x=0,f=1; char ch=getchar(); 9 while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); } 10 while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } 11 return x*f; 12 } 13 const int mod=1e9+7,NN=1e5+5; 14 int n,opt,w[NN],ans1,ans2,ll[NN],rr[NN]; 15 int pw[35],f[NN][35]; 16 stack<int> s,t; 17 struct tree{ 18 int ch[NN*22][2],siz[NN*22],root[NN*22],node; 19 void insert(int pre,int &now,int i,int x){//前驱点 当前点 最大递归位数 插入值 20 now=++node; 21 siz[now]=siz[pre]; 22 if(i<0){siz[now]++;return;} 23 int bo=(x>>i)&1; 24 ch[now][bo^1]=ch[pre][bo^1]; 25 insert(ch[pre][bo],ch[now][bo],i-1,x); 26 siz[now]=siz[ch[now][0]]+siz[ch[now][1]]; 27 } 28 void insert(int x,int pos){insert(root[pos-1],root[pos],20,x);} 29 int query(int x,int y,int p){//在x～y区间内的1的个数 30 int pos=root[p],ans=0; 31 for(int i=20;i>=0;i--){ 32 int a=(x>>i)&1,b=(y>>i)&1; 33 if(!b){ 34 ans+=siz[ch[pos][a^1]]; 35 pos=ch[pos][a]; 36 }else pos=ch[pos][a^1]; 37 if(!pos) break; 38 } 39 return ans; 40 } 41 }trie; 42 void work(int k,int l,int r){ 43 for(int i=0;i<=20;i++){ 44 int pre1=f[k][i]-f[l-1][i],pre0=k-l+1-pre1,nxt1=f[r][i]-f[k-1][i],nxt0=r-k+1-nxt1; 45 ans1=(ans1+pw[i]*(pre1*nxt0%mod+pre0*nxt1%mod)%mod*w[k]%mod)%mod; 46 } 47 } 48 void search(int k,int l,int r){ 49 if(k-l<r-k){ 50 for(int i=l;i<=k;i++) 51 ans2=(ans2+(trie.query(w[i],w[k],r)-trie.query(w[i],w[k],k-1))*w[k]%mod)%mod; 52 } 53 else{ 54 for(int i=k;i<=r;i++) 55 ans2=(ans2+(trie.query(w[i],w[k],k)-trie.query(w[i],w[k],l-1))*w[k]%mod)%mod; 56 } 57 } 58 namespace WSN{ 59 inline int main(){ 60 n=read(),opt=read(); 61 for(int i=1;i<=n;i++) {w[i]=read();trie.insert(w[i],i);} 62 pw[0]=1; 63 for(int i=1;i<=20;i++) pw[i]=2*pw[i-1]; 64 for(int i=1;i<=n;i++){ 65 while(!s.empty()&& w[i]>w[s.top()]) s.pop(); 66 if(s.empty()) ll[i]=1; 67 else ll[i]=s.top()+1; 68 s.push(i); 69 } 70 for(int i=n;i>=1;i--){ 71 while(!t.empty()&& w[i]>=w[t.top()]) t.pop(); 72 if(t.empty()) rr[i]=n; 73 else rr[i]=t.top()-1; 74 t.push(i); 75 } 76 for(int i=1;i<=n;i++) for(int j=0;j<=20;j++) 77 {f[i][j]+=f[i-1][j]; if((w[i]>>j)&1) f[i][j]++;} 78 for(int i=1;i<=n;i++) work(i,ll[i],rr[i]); 79 for(int i=1;i<=n;i++) search(i,ll[i],rr[i]); 80 if(opt==1) write(ans1); 81 else if(opt==2) write(ans2); 82 else {write(ans1); write(ans2);} 83 return 0; 84 } 85 } 86 signed main(){return WSN::main();} 87 // FILE *A=freopen("english3.in","r",stdin); 88 // FILE *B=freopen("aaa.out","w",stdout);
End
此次考试较为上次聪明了一点，总归是并没有执着于正解而不去打暴力，可是对于正解的思考还是较少，下次考试应该注意打暴力的速度和正确性以及留给正解的思考时间
浙公网安备 33010602011771号