【集训队作业2018】count 题解

【集训队作业2018】count 题解

感觉这是好题，但是九日写的过于抽象，写个宝宝版

首先容易发现这个同构条件其实就是建出笛卡尔树之后一样

注意到如果 \(n \ge m\) 时一个数 \(x\) 出现了多次，先离散化，如果存在没出现的数的话将相等除了第一个数以外的数和所有大于 \(x\) 的数都加一，树的形态不变

所以我们不怕数用不完，只怕数不够用，为了节省数字，可以贪心的将每一层都染上相同颜色，大概这个样子

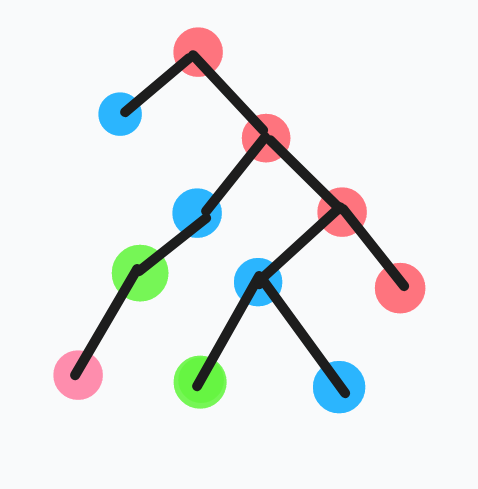
这样就非常直观了，我们现在可以简单的记录上一层的节点个数之类的做到多项式复杂度

注意到可以把树链压起来，刚才的图搞完就是这个样子

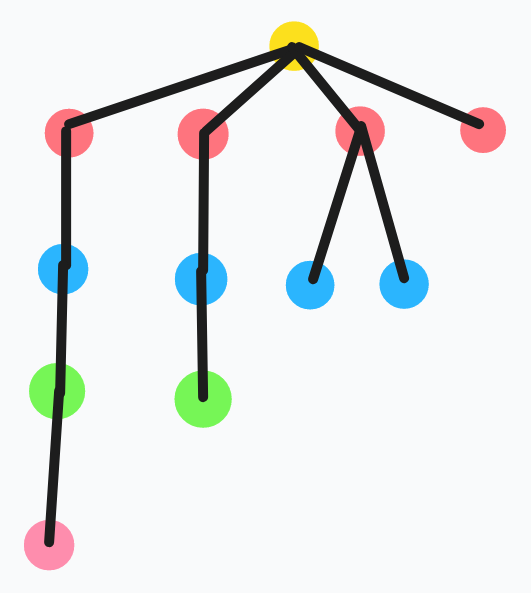
不难发现这是一个双射，于是就可以直接计数括号序了，就是一个反射容斥板子，感觉上也可以随便 \(O(n \operatorname{polylog}(n))\) 求一行