联合省选 2024 Day2T1 迷宫守卫 题解

联合省选 2024 Day2T1 迷宫守卫 题解

好像距离联合省选已经半年了，前两天看到这题才想起来改，距离分班已经半年了，也算是好好学了半年了，但是还是那么菜，有点绷不住，感觉不如文化课

后来翻到题解区第二篇题解才知道自己赛时想的反悔贪心其实是正解，但是当时啥也不会，主要是不会实现，加上当时实现思路也有点问题，又不会分析复杂度，当时狂想写，但是狂挂不止

回到反悔贪心 ：

Part 1 思路

首先，Bob会选定一个目标点，向着目标点走来获取符文，由于字典序的性质，他一定首选 \(1\) 此时只有两种情况

1. Alice 可以通过唤醒守卫来阻止 Bob 拿到 \(1\)
2. Bob 可以顺利拿到 \(1\)

假如说是情况 1，那么 Bob 一定不会选择 \(1\)，因为 Alice 一定会把先 \(1\) 堵上，我们顺次考虑2、3、4...即可

如果说是情况二，Bob会走到 \(1\) 对应的叶子，而 Alice 不能做出任何决定，答案的第一位也就确定了

之后的子树内递归进行此操作即可

问题在于 Alice 可能会有多种方式来堵上字典序小的那些数，假如说她无脑选择当前价值最小的，可能会因为作用域太小而得到较劣的解

那么我们可以先贪心选择对当前局面有最好影响的价值和最小方案，等到该决策失效的时候再考虑将其更换

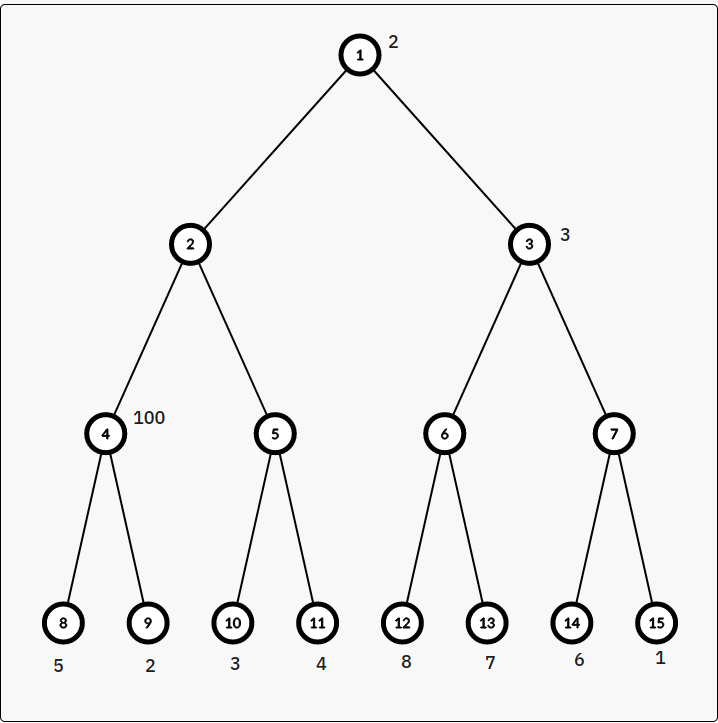
以上图为例，假如我们只有三的权值，那么根据贪心策略，会先选唤醒根节点的守卫，可是我们发现这样的答案是

2 5 3 4 1 6 7 8

但是假如我们唤醒节点 \(3\) 的守卫，答案就会变成

2 5 3 4 7 8 1 6

显然后者更优，这是因为后者深度更大，守卫的子树规模较小，但是守卫的持续时间也更长，所以一旦走入一个守卫的守护范围，我们就要反悔，考虑将它换成若干个深度较大的守卫，这符合我们先保证高位大，后尽量顺次考虑的要求，这里证明也挺容易的

Part2 代码框架

对于决定这个目标点，我们发现是单调的，直接二分就好，对于顺次跳链，dp等做法暂时不进行介绍

二分的check 可以写 \(O(n)\) 的 dp,求出答案为当前值最小的代价能否承受即可，转移啥的是显然的

我们对于二分的点，直接走到那个节点，容易发现走的链将树分割成 \(1\)，\(2\)，\(3\)，\(4\)，\(h-1\)... 的好多不同规模的子树，递归做，进去之前把之前决策对比一下撤销就完了

考虑分析复杂度,设 \(f(h)\) 是解决一棵高度为 \(h\) 的子树的复杂度，有

\[f(h)=h2^h+\sum \limits _{i=1}^{h-1} f(i) \]

给它分个组，得到

\[f(h)=h2^h+\sum \limits _{i=1}^{h-2} f(i)+f(h-1) \]

又有

\[f(h-1)=\sum \limits _{i=1}^{h-2} f(i)+(h-1)2^{h-1} \]

也就是说

\[f(h)=h2^h+2f(h-1)-(h-1)2^{h-1} \]

扔掉减号后面的部分就能的到复杂度上界，发现第 \(i\) 层分裂出来的复杂度是 \(O(i2^h)\)，一共 \(h\) 层，所以单次复杂度为 \(O(n^22^n)\) 完全可以接受

其实我们还可以做到更优，考虑复杂度大头在每次都要重新 dp，浪费了很多有意义信息，我们发现对于一个子树内，其实 让答案 \(\ge k\) 的代价和让答案 \(\ge d\) 的代价完全一样，这里 d 是当前这棵树子树内第一个 \(>k\) 的数，所以我们可以直接预处理 dp，预处理复杂度 \(O(n2^n)\)，之后所有二分和贪心步骤都不需要再跑一遍 dp，所以之后反悔贪心复杂度也是 \(O(n2^n)\)，即总复杂度 \(O(n2^n)\)

Part3 实现

这题想明白之后实现其实不难，考虑每次从底向上跳，其实主要是捋清楚思路，想明白什么时候撤销，应该怎样撤销

赛时甚至一直试图记录下来每次贪心后选取的点，后来因为太难写，完全不敢也不会写这个做法最后写了删删了写，还是只糊了暴力

贴个代码

CODE

#include<bits/stdc++.h>
#define llt long long
const llt N=201000;
using namespace std;
llt T,n,k,w[N],Q[N],dp[N][2],sum,to[N];vector<llt> vec,ans;bool jud[N];
void solve(llt,llt);
void DP(llt now,llt pl,llt h)
{
    dp[now][0]=dp[now][1]=0;
    if(h==n)    
    {
        if(Q[now<<1|1]<pl)   dp[now][0]=w[now],dp[now][1]=0;
        if(Q[now<<1]<pl)    dp[now][0]=1e18,dp[now][1]=0;
        return;
    }
    DP(now<<1|1,pl,h+1),DP(now<<1,pl,h+1);
    dp[now][1]=min(dp[now<<1|1][1],dp[now<<1|1][0])+min(dp[now<<1][1],dp[now<<1][0]);
    dp[now][0]=min(dp[now<<1][0]+dp[now<<1|1][1]+w[now],dp[now<<1][0]+dp[now<<1|1][0]);
}
llt find(llt now,llt h)
{
    llt l=0,r=vec.size()-1,mid;
    while(l<r)
    {
        mid=l+r+1>>1;
        DP(now,vec[mid],h);
        if(dp[now][0]<=k-sum)   l=mid;
        else r=mid-1;
    }
    DP(now,vec[l],h);sum+=dp[now][0];
    return vec[l];
}
void jump(llt now,llt pl,llt h,llt root)
{
    jud[now]=1;
    DP(now,pl,h);
    if(jud[now<<1|1]) sum-=dp[now<<1][0],solve(now<<1,h+1);
    else
    {
        sum-=min(dp[now<<1|1][0],w[now]);
        if(dp[now<<1|1][0]+sum>k)   sum+=w[now],solve(now<<1|1,h+1);
        else solve(now<<1|1,h+1);
    }
    if(now==root)    return;
    jump(now>>1,pl,h-1,root);
}
void solve(llt now,llt h)
{
    if(h>n) {ans.push_back(Q[now]);return;}
    vector<llt>().swap(vec);
    for(int i=(1<<n-h+1)*now,j=1;j<=(1<<n-h+1);i++,j++)
        vec.push_back(Q[i]);
    sort(vec.begin(),vec.end());
    llt oo=find(now,h);
    ans.push_back(oo);jud[to[oo]]=1;
    jump(to[oo]>>1,oo,n,now);
}
int main()
{
    #ifdef LOCAL
        freopen("1.in","r",stdin);
        freopen("1.out","w",stdout);
    #endif
    scanf("%lld",&T);
    while(T--)
    {
        vector<llt>().swap(ans);sum=0;memset(dp,0,sizeof(dp));
        scanf("%lld%lld",&n,&k);
        for(int i=1;i<(1<<n);i++)   scanf("%lld",&w[i]);
        for(int i=(1<<n);i<(1<<n+1);i++)   scanf("%lld",&Q[i]),to[Q[i]]=i;
        solve(1,1);
        for(auto v:ans) printf("%lld ",v);puts("");
        memset(jud,0,(1<<n+1)*sizeof(bool));
    }
    return 0;
}