[考试反思]0504省选模拟87：开花

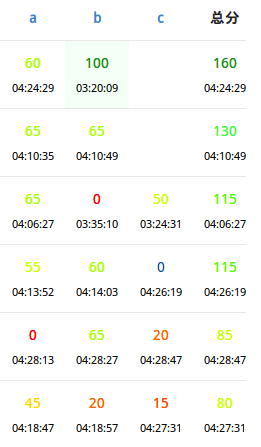
题是挺好的。就是我太菜了。

$T2$能爆零也是弱智到一定程度了。。。

写炸一个变量名$k$写成$n$了，结果弱智样例恰好满足$k=n$，然后就爆零了。$gpwy$

如果这$60$没挂还能蹭个$rk1$。然而貌似考不到$rk1$已经是常态了。。。

这次$T3$还行。由于大神们都不屑于看构造的课件而只有我去看了那个没啥用的玩意。

于是得到的最大收获：乱搞，猜结论。

然后就瞎猜，花了不少时间猜了个结论并且写了一个假的构造（然而其实想到$dinic$了但是因为并不清楚结论对不对，写大$dinic$怪亏的）

然而不会处理$k$为偶数的情况，于是继续乱搞，获得了额外的$10pts$。不写$dinic$挂了$5pts$。总体而言问题不大。

就是$T2$问题有点大。低错还在犯啊。。。

多手几个模样例的习惯该搬回来了啊。

 

T1：a

大意：有一个变量$z=0$。$n$轮每轮有$p_i(0 \le i \le k)$的概率$z+=i$。问最后$min(x,z)$的期望。$kx \le 5 \times 10^7,x \le 10^7, k \le 100,n \le 10^7$

首先可以想到这个类似背包的东西可以生成函数，然后如果不考虑取$min$的话，可以直接多项式快速幂。$O(x\ log\ x\ log\ n)$那种可以得到$65pts$

进一步可以发现，其实我们并不在意超过$x$的项。设$Q=P^n$则有$ans=\sum\limits_{i=0}^{x-1} [x^i]Q \times i + x \times (1-\sum\limits_{i=0}^{i-1} [x^i]Q )$

所以多项式快速幂的时候可以取模。然后继续发现一些奇怪的事情。直接想不能优化，于是我们尝试对$P^{n+1}$求导

首先$(P^{n+1})' = ((P)^{n+1})'$。其中$P$看作一个函数，运用复合函数求导法则得到$(n+1)P'Q$

然后$P^{n+1} = P \times P^{n}$。运用乘法求导公式得到$P'Q+Q'P$

自然两个结果可以画等号，所以我们得到$nP'Q=PQ'$。$P,P'$为已知。$[x^0]Q$是易知的。所以我们可以依据这个式子推得$[x^0]Q'$。进而知道$[x^1]Q$。逐层递推。

因为$P$只有$k$项$Q$只有$x$项。所以总复杂度是$O(kx)$的。

#include<cstdio>
#define mod 998244353
#define S 10000007
int P[102],p[102],Q[S],q[S],n,k,x,tot,I,ans,iv[S];
int qp(int b,int t,int a=1){for(;t;t>>=1,b=1ll*b*b%mod)if(t&1)a=1ll*a*b%mod;return a;}
int main(){
    scanf("%d%d%d",&n,&k,&x);
    iv[1]=1;
    for(int i=2;i<=x;++i)iv[i]=mod-1ll*mod/i*iv[mod%i]%mod;
    for(int i=0;i<=k;++i)scanf("%d",&P[i]),tot+=P[i];
    for(int i=0;i<=k;++i)P[i]=1ll*P[i]*qp(tot,mod-2)%mod;
    for(int i=0;i<k;++i)p[i]=(i+1ll)*P[i+1]%mod;
    I=qp(P[0],mod-2); Q[0]=qp(P[0],n); ans=1ll*Q[0]*(mod-x)%mod;
    for(int i=0;i<x;++i){
        for(int j=i;~j&&j>i-k;--j)q[i]=(q[i]+1ll*Q[j]*p[i-j])%mod;
        q[i]=1ll*q[i]*n%mod;
        for(int j=i-1;~j&&j>=i-k;--j)q[i]=(q[i]-1ll*q[j]*P[i-j])%mod;
        q[i]=(q[i]+mod)*1ll*I%mod; Q[i+1]=q[i]*1ll*iv[i+1]%mod;
        ans=(ans+Q[i+1]*(mod-x+i+1ll))%mod;
    }printf("%d\n",(ans+x)%mod);
}

 

T2：b

大意：最开始你有$n$个$0$和$n$个$1$。执行如下过程$2n$次：如果你$0,1$都有那就$50\%$的概率将其中一个放在序列上。否则有啥放啥。

多次询问求$P(a_1=a_2=...=a_k)$。$n,q \le 10^5,k \le 2 \times 10^5$

$\sum k$不大，那么$k$最多也就$O(\sqrt{\sum k})$种。

先考虑一个暴力，对于一个已知序列，它出现的概率，设$a_{2n}^1$的最后一次出现的位置为$x$，则概率为$2^{-x}$

故直接暴力的话枚举每种数的完结位置乘组合数就行了。

然后处理一堆$\binom{j}{n-i} \times 2^{-j}$和对于每个$k$处理$\binom{j}{n-k-i} \times 2^{-j}$这类的东西就可以$O(k\sqrt{k})$预处理后$O(k)$计算了。

懒得搬式子了。需要处理$a_k=2n$的边界。

#include<bits/stdc++.h>
using namespace std;
#define S 200005
#define mod 998244353
vector<int>a[S],s2[S]; set<int>K;
int k[S],n,q,fac[S],inv[S],pw[S],ipw[S],s[S];
int qp(int b,int t,int a=1){for(;t;t>>=1,b=1ll*b*b%mod)if(t&1)a=1ll*a*b%mod;return a;}
int C(int b,int t){return t<0||t>b?0:fac[b]*1ll*inv[t]%mod*inv[b-t]%mod;}
int main(){
    scanf("%d%d",&n,&q);
    for(int i=1;i<=q;++i){
        scanf("%d",&k[i]); K.insert(k[i]);
        for(int j=1,x;j<=k[i];++j)scanf("%d",&x),a[i].push_back(x);
        sort(a[i].begin(),a[i].end());
    }
    for(int i=fac[0]=pw[0]=1;i<S;++i)fac[i]=fac[i-1]*1ll*i%mod,pw[i]=2*pw[i-1]%mod;
    inv[S-1]=qp(fac[S-1],mod-2); ipw[S-1]=qp(pw[S-1],mod-2);
    for(int i=S-2;~i;--i)inv[i]=inv[i+1]*(i+1ll)%mod,ipw[i]=ipw[i+1]*2%mod;
    for(int i=1;i<=n+n;++i)s[i]=(s[i-1]+1ll*C(i,n-1)*ipw[i])%mod;
    for(auto k:K){
        s2[k].resize(n+n+1); s2[k][0]=n==k+1;
        for(int i=1;i<=n+n;++i)s2[k][i]=(s2[k][i-1]+1ll*C(i,n-1-k)*ipw[i])%mod;
    }
    #define A(i) a[_][i]
    for(int _=1;_<=q;++_){
        int K=k[_],ans=0; a[_].push_back(n+n);
        if(A(K-1)!=n+n)ans=(ans+C(A(K-1)-K,n-K)*1ll*ipw[A(K-1)])%mod;
        if(A(0)>=2)ans=(ans+s[A(0)-2]*1ll*ipw[1])%mod;
        for(int i=0;i<K;++i)if(A(i+1)>A(i)+1)ans=(ans+1ll*ipw[i+2]*(mod+s[A(i+1)-i-3]-(A(i)-i-2>=0?s[A(i)-i-2]:0)))%mod;
        if(A(K-1)!=n+n)ans=(ans+1ll*ipw[K+1]*(s2[K][n+n-K-2]-(A(K-1)-K-1>=0?s2[K][A(K-1)-K-1]:0)+mod))%mod;
        printf("%d\n",ans*2%mod);
    }
}

 

T3：c

大意：对于所有$popcnt \le k$的$< 2^n$的二进制数，将其分成尽量少的组，使得每组中任意两元素交集为空，整组并集$\le k$。$n,k \le 17$

先考虑$k$是奇数。

首先对于任意$i>\frac{k}{2}$，这样的数称之为大数的话，那么显然大数不会与大数配对，也就是说组数的下限是大数个数。

然后发现有$\binom{n}{i} \le \binom{n}{k-i}$也就是再说，小数的个数不超过大数。

根据$Hall$感性理解或者口胡证明，可知所有大小为$i$的小数都能不重复的与$k-i$的大数匹配，也就是完美匹配。

答案到达下界一定最优。跑个$dinic$构造即可。

如果$k$是偶数，就存在那种大不大小不小的数。也就是大小为$\frac{k}{2}$的数，它要与大小为$\frac{k}{2}$的数配对。

别的都是二分图匹配但是这个是一般图匹配。

所以可以直接上带花树。大概的意思就是把所有点黑白染色。

出问题的地方就是出现了奇环，于是把它缩成一个点来代表它们。

一个更加神奇的做法是随机化：在$uoj$上都$hack$不掉。随机一组就过了，时空及码长也很优秀。好像多数人写的都是这个。

反正我不会开花。但是牛开花了。有空必须写带开花树的时候还得骚扰他（虽说大概没人卡随机化，好像也不是很好卡）

source：link

#include<bits/stdc++.h>
using namespace std;
#define S 111111111
#define N (1<<17)+1
int n,k,sz[N],ans,b[N][3],fir[N],l[S],to[S],d[N],T,ec,q[N],al[N],mt[N];bool w[S];
vector<int>V[18],E[N];
void print(int s){for(int i=0;i<n;++i)if(s>>i&1)putchar('a'+i);putchar(' ');}
void link(int a,int b,int x){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;w[ec]=x;}
void con(int a,int b){link(a,b,1);link(b,a,0);}
bool bfs(){
    for(int i=1;i<=T;++i)d[i]=T;
    for(int h=1,t=1;h<=t;++h)for(int i=fir[q[h]];i;i=l[i])if(d[to[i]]>d[q[h]]+1&&w[i])
        d[q[++t]=to[i]]=d[q[h]]+1;
    return d[T]<T;
}
int dfs(int p,int f){int r=f;
    if(p==T)return f;
    for(int i=fir[p];i&&r;i=l[i])if(w[i]&&d[to[i]]==d[p]+1){
        int x=dfs(to[i],1);
        if(!x)d[to[i]]=T;
        else w[i]=0,w[i^1]=1,r--;
    }return f-r;
}
int DFS(int p,int f){
    random_shuffle(E[p].begin(),E[p].end()); al[p]=f;
    for(int i=0,y,z;i<E[p].size();++i){
        y=E[p][i];z=mt[y];
        if(al[z]==f)continue;
        mt[p]=y; mt[y]=p; mt[z]=0;
        if(!z||DFS(z,f))return 1;
        mt[p]=0; mt[y]=z; mt[z]=y;
    }return 0;
}
int main(){
    scanf("%d%d",&n,&k);T=1<<n;
    const int M=(1<<n)-1;
    for(int i=1;i<=M;++i)sz[i]=sz[i^i&-i]+1;
    for(int i=1;i<=M;++i)if(sz[i]<=k)V[sz[i]].push_back(i);
    for(int i=0;i<V[k].size();++i)b[++ans][0]=1,b[ans][1]=V[k][i];
    for(int i=1;i+i<k;++i){
        ec=1;fir[0]=fir[T]=0;
        for(int j=0;j<V[i].size();++j)for(int u=M^V[i][j],z=u;z;z=z-1&u)if(sz[z]==k-i)con(V[i][j],z);
        int E=ec;
        for(int j=0;j<V[i].size();++j)con(0,V[i][j]);
        for(int z=0;z<V[k-i].size();++z)con(V[k-i][z],T);
        while(bfs())dfs(0,T);
        for(int j=2;j<=E;j+=2)if(!w[j])b[++ans][0]=2,b[ans][1]=to[j],b[ans][2]=to[j^1];
        for(int j=fir[T];j;j=l[j])if(!w[j])b[++ans][0]=1,b[ans][1]=to[j];
    }
    if(!(k&1)){
        for(int j=0;j<V[k/2].size();++j)for(int u=M^V[k/2][j],z=u;z;z=z-1&u)if(sz[z]==k/2)
            E[V[k/2][j]].push_back(z),E[z].push_back(V[k/2][j]);
        for(int j=0;j<V[k/2].size();++j)if(!mt[V[k/2][j]])srand(time(0)),DFS(V[k/2][j],V[k/2][j]);
        for(int j=0;j<V[k/2].size();++j)if(!mt[V[k/2][j]])b[++ans][0]=1,b[ans][1]=V[k/2][j];
            else if(mt[V[k/2][j]]>V[k/2][j])b[++ans][0]=2,b[ans][1]=V[k/2][j],b[ans][2]=mt[V[k/2][j]];
    }
    printf("%d\n",ans);
    for(int i=1;i<=ans;++i){
        printf("%d ",b[i][0]);
        for(int j=1;j<=b[i][0];++j)print(b[i][j]);
        puts("");
    }
}