[考试反思]0324省选模拟54：缺失

来了一场既没有$c++11$也没有$O2$的考试。

然后喜闻乐见的出现了一些$CE$，以及被卡常的。

然而与我没有关系，$T1$想到了最高的一档暴力（正解被卡常除外）

然而里面用到了$map$，没$O2$跑的是真的慢，最后拿了个不高不低的$50pts$

然后$T2$是神仙题，$O(n^3)$的$dp$我是天生恐惧。就算改题也是尝试理解了好久。

然后牛一直说它简单，然而给我讲并没有听明白。

哭了，太菜了听啥都像嘲讽。他们不懂底层人民的生活。

虽说我到现在都不明白暴力为什么会挂。

$T3$的最高分$20$居然是信仰的$puts("0")$。数据真神奇，然后还有的人$5pts$思路挺神仙的。。

正解更神仙，完全想不到。

考后改题时间都砸$T2$上了，到处问问了两个半小时只有一个人给我讲，还没讲明白（不敢继续问了23333

后来发现$T1$比较简单就把$T1$弄了下来，然后继续到处问$T2$。很晚很晚才问明白然后$AC$

然后就没时间搞$T3$了。大概思想明白。可以看看$AK$神们的博客。

状态还是很差。快点调整回来啊！！！

 

T1：space

大意：四维空间，有四个排列$A,B,C,D$。$(i,j,k,l) \rightarrow (A_i,B_j,C_k,D_l)$的代价为$1$。其余代价为$2$。求最小代价的经过所有点的回路。$n \le 10^5$

排列交换当成建图貌似渐渐成为了套路。？

如果我们对四个维度所有点一起连边，那么最后的代价就是$n^4+$环的个数。

每个四维环都是由四个一维环拼接出来的。改变定义设$A_i$表示大小为$i$的环有多少个。

$ans=n^4+A_iB_jC_kD_l\frac{i,j,k,l}{lcm(i,j,k,l)}$

$A$的数量级别是$O(\sqrt{n})$的。所以总复杂度是$O(n^2logn)$的。

然后对前后两个一组分组，$meet  \ in \ middle$。

大概是个莫反。对于每种质因子考虑可以得到$\frac{abcd}{lcm(a,b,c,d)} = gcd(a,b)gcd(c,d)gcd(lcm(a,b),lcm(c,d))$

这样就可以把前后两部分分开。$(A_i,i,B_j,j) \rightarrow (A_iB_jgcd(i,j),lcm(i,j))$。得到新的二元组。

然后问题就在于二元组合并。懒得写公式了：

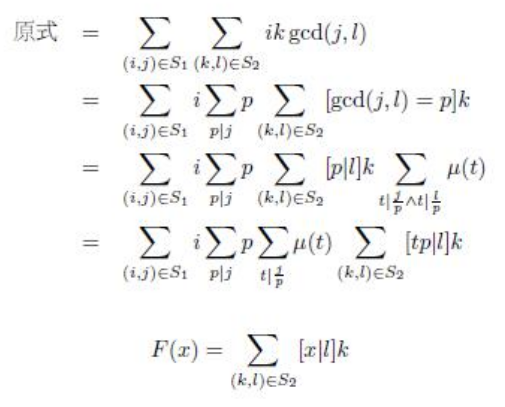
最后面的只与$Q$有关。可以预处理。我们对于每个$pair$把$second$分解质因数这样就能在合法的复杂度内求出$\varphi$和枚举约数。

然后就没了。但是因为没开$O2$所以$STL::map$超慢。手写哈希表是必要的（存$F$用）

#include<bits/stdc++.h>
using namespace std;
#define S 211111
#define mod 998244353
int w[S],al[S],n,ans,A[S],B[S],C[S],D[S],a[S],b[S],c[S],d[S],X,Y,T[S];
vector<int>_dv[S],_t[S];
struct hashmap{
    #define $ 10000007
    int fir[$],l[$],to[$],v[$],ec;
    int&operator[](int x){int r=x%$;
        for(int i=fir[r];i;i=l[i])if(to[i]==x)return v[i];
        l[++ec]=fir[r];fir[r]=ec;to[ec]=x;return v[ec];
    }
}F;
int mo(int x){return x>=mod?x-mod:x;}
int gcd(int a,int b){return b?gcd(b,a%b):a;}
struct s{
    int a; vector<int>b,t;
    void init(int x,int y,int z,int w){
        a=1ll*x*y*gcd(z,w)%mod;
        for(int i=0;i<_dv[z].size();++i)T[_dv[z][i]]=max(T[_dv[z][i]],_t[z][i]);
        for(int i=0;i<_dv[w].size();++i)T[_dv[w][i]]=max(T[_dv[w][i]],_t[w][i]);
        for(int i=0;i<_dv[z].size();++i)b.push_back(_dv[z][i]), t.push_back(T[_dv[z][i]]),T[_dv[z][i]]=0;
        for(int i=0;i<_dv[w].size();++i)if(T[_dv[w][i]])b.push_back(_dv[w][i]), t.push_back(T[_dv[w][i]]),T[_dv[w][i]]=0;
    }
}x[S],y[S];
int read(){
    register int p=0;register char ch=getchar();
    while(!isdigit(ch))ch=getchar();
    while(isdigit(ch))p=(p<<3)+(p<<1)+ch-48,ch=getchar();
    return p;
}
void init(int*M,int*m){
    for(int i=1;i<=n;++i)w[i]=read(),al[i]=0;
    for(int i=1;i<=n;++i)if(!al[i]){
        int p=i,c=1;al[p]=1;
        while(!al[w[p]])p=w[p],al[p]=1,c++;
        M[c]++;
    }for(int i=1;i<=n;++i)if(M[i])m[++m[0]]=i;
}
void ctb(int o,int n,int w){
    if(n==y[o].t.size()){F[w]=mo(F[w]+y[o].a);return;}
    for(int j=0;j<=y[o].t[n];++j)ctb(o,n+1,w),w*=y[o].b[n];
}
int ask(int o,int n,int w,int phi,int ans=0){
    if(n==x[o].t.size())return 1ll*F[w]*phi%mod;
    for(int j=0;j<=x[o].t[n];++j)ans=mo(ans+ask(o,n+1,w,phi)),w*=x[o].b[n],phi=1ll*phi*(x[o].b[n]-(j?0:1));
    return ans;
}
int main(){//freopen("space20.in","r",stdin);
    cin>>n;init(A,a);init(B,b);init(C,c);init(D,d);
    for(int i=2;i<=n;++i)if(_dv[i].empty())for(int j=i;j<=n;j+=i){
        int x=j,c=0;_dv[j].push_back(i);
        while(x%i==0)c++,x/=i; _t[j].push_back(c);
    }
    for(int i=1;i<=a[0];++i)for(int j=1;j<=b[0];++j)x[++X].init(A[a[i]],B[b[j]],a[i],b[j]);
    for(int i=1;i<=c[0];++i)for(int j=1;j<=d[0];++j)y[++Y].init(C[c[i]],D[d[j]],c[i],d[j]);
    for(int i=1;i<=Y;++i)ctb(i,0,1);
    for(int i=1;i<=X;++i)ans=(ans+1ll*x[i].a*ask(i,0,1,1))%mod;
    cout<<(ans+1ll*n*n%mod*n%mod*n)%mod<<endl;
}

 

T2：party

大意：树上有些点上有人，要求移动后形成一个联通块。（每点最多一个人）最小化总移动距离。$n \le 200$

神仙神仙神仙题。

设$dp[i][j]$表示，以$i$为根的子树中，不考虑$i$节点上的人，剩下在子树内形成了一个大小为$j$的联通块的最小代价。

默认剩下的$cnt-j$个人都围在$i$点上，且不考虑从$i$子树外到达$i$所用的步数。

那么在我们枚举一个根节点之后进行$dp$。考虑加入一个子树时会发生什么：

1）最后这个子树里一个人也没有。$dp[i][j]+=dp[son][0]+cnt[son]$。就是所有堆在$son$的人都上涌到$i$。因为不考虑从上面来的代价，所以只有$cnt[son]$有代价。

2）枚举这个子树里最后有多少人。$dp[i][j]=\min\limits_{k=1}^{j} (dp[i][j],dp[i][j-k]+dp[son][k]+ | k-sz[son] | )$

这里的绝对值非常妙。因为让外部走入和从内部走出的代价都是这个差值。

具体实现类似于一个背包。为了本层只更新本层，所以要倒着枚举$j$。

总的时间复杂度是$O(n^3)$的。

 

T3：wang

大意：要求设计值域定义域均为$Z$的函数$F$满足$F(2F(x)-x+1)=F(x)+C$。（$C$为给定常数）。给定$n$对$(X,Y)$要求最小化$\sum\limits_{i=1}^{n} | F(X_i) - Y_i |$

这个函数的奇怪性质肯定有好多要研究的地方。函数嵌套非常不爽，于是我们设$y=2F(x)-x+1$

现在代回去好看一些：$F(y)=x+C$。

两边同时$+C:F(y)+C=x+2C$

然后等式左边就变成了原始式子右边的形式，推回到左边来得到：$F(2F(y)-y+1)=x+2C$

把左边的$2F(y)$再代回$F(y)=F(x)+C$。剩余的$y$代回$y=2F(x)-x+1$

然后惊喜的发现式子就只剩下了$F(x+2C)=F(x)+2C$

这是个好性质。我们可以把括号内外的$2C$丢进来或撇出去。那么最简单的想法就是，在外部加上等量数后，内部可以对$2C$取模。

也就是说，只要确定了$F(x)$的值，那么$F(x+2C),F(x+4C)...$就都确定了。

所以说其实我们可以把$F(x)$表示为$t+nC$的形式。其中$0 \le t < 2C$。至此还有两种表示方法，但是先往下看着。

$F(2F(x)-x+1)=F(x)+C$

可以代换了：$F(2t+2nC-x-1)=t+nC+C$

然后上面已经说明$2C$可以提出，那么左边的$2nC$就可以拿出来了：$F(2t-x-1)+2nC=t+nC+C$

也就是$F(2t-x+1)=t-nC+C$

我们发现这时候在函数自变量里的$x$由正变为了负，我们把正的一项加回来，就能得到$F(x)+F(2t-x+1)=2t+C$

换句话说，对于任意一对奇数偶数，若$a+b=2t+1,F(x)=t+nC$那么就有$F(a)+F(b)=2t+C$

所以说，在$F(x)=t+nC(0 \le t <2C)$的两种表达方式中，其中一种没什么用，而$t,x$奇偶性不同的那一种它有所限制。（当然两种表达形式都是成立的

而我们又限定了$0 \le t <2C$，也就是说，每个奇数一定对应某个特定偶数。某个偶数一定对应特定奇数。

一旦$F(x)=t+nC$确定，那么$F(2t+1-x)$也就同时确定了。这也可见，对应关系是双向的，且每个数的度数均为一。

于是我们就知道，$C$个奇数与$C$个偶数之间，存在完美匹配。这就是二分图匹配问题。

回归原问题，我们要最小化纵坐标的差绝对值。我们所需要决定的只是配对关系，配对关系确定$t$也就确定了，然后$n$只要取该配对关系下的最优值即可。

我们确定其中一个配对关系之后，那么这两个点的$F$值就同时确定了，模$2C$之后横坐标对应这两个点的代价也就确定了。

所以说每种配对的贡献是可以分开计算的。我们现在来考虑某个配对$a,b$的代价。这就是我们配对时这条边的边权。

沿用上面的定义，$a+b=2t+1$

那么对于所有模$2C$后是偶数$a$的点$(X_i,Y_i)$，它贡献的代价是$| \lfloor \frac{X_i}{2C} \rfloor \times 2C + F(a) -Y_i|$

如果$F(a)=t+nC$那么就有$| \lfloor \frac{X_i}{2C} \rfloor \times 2C + t+nC -Y_i|$

同时$F(b)$也就确定了，是$2t+C - F(a) = t -nC + C$

那么对于所有模$2C$后是偶数$a$的点$(X_i,Y_i)$，它贡献的代价是$| \lfloor \frac{X_i}{2C} \rfloor \times 2C + F(b) -Y_i|$

即为$| \lfloor \frac{X_i}{2C} \rfloor \times 2C + t-nC+C -Y_i|$

两种贡献中未知量只有$n$。我们把第二个式子的形式变一下：

绝对值内取相反数结果不变，那么就是$| -  \lfloor \frac{X_i}{2C} \rfloor \times 2C - t + nC  - C +Y_i|$

这样，我们需要的就是一个合适的$n$值使两种贡献加起来尽量小。

考虑另一个经典的问题模型：已知若干$x_i$，求一个$x$,最小化$\sum\limits |x_i -x|$。答案是$x$是$x_i$的中位数

在这里也只需要让$nC$尽量成为上述两种表达式对应的所有值的中位数即可。

然后就只需要一个$MCMF$来进行最大权匹配了。

#include<bits/stdc++.h>
using namespace std;
#define S 66666
int n,C,CC,_x,xa,xb,xp,_y,ya,yb,yp,fir[123],l[S],to[S],v[S],ec=1,q[S],iq[123];
long long w[S],d[S],ans,f[S];
void link(int a,int b,int V,long long W){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;v[ec]=V;w[ec]=W;}
void con(int a,int b,long long W){link(a,b,1,W);link(b,a,0,-W);}
vector<int>X[123],Y[123];
bool bfs(){
    memset(d,0x3f,sizeof d); memset(iq,0,sizeof iq); d[CC]=0; q[1]=CC;
    for(int h=1,t=1;h<=t;iq[q[h++]]=0)for(int i=fir[q[h]];i;i=l[i])if(v[i]&&d[to[i]]>d[q[h]]+w[i]){
        d[to[i]]=d[q[h]]+w[i]; if(!iq[to[i]])iq[q[++t]=to[i]]=1;
    }return d[CC+1]<1e17;
}
int dfs(int p,int f){int r=f;
    if(p==CC+1)return f; iq[p]=1;
    for(int i=fir[p];i&&r;i=l[i])if(v[i]&&d[to[i]]==d[p]+w[i]&&!iq[to[i]]){
        int x=dfs(to[i],1);
        if(!x)d[to[i]]=-1;
        else v[i]--,v[i^1]++,ans+=w[i],r--;
    }return f-r;
}
long long cal(int a,int b){
    int c=0,t=a+b>>1,nC1,nC2;long long f1=0,f2=0;
    for(int i=0;i<X[a].size();++i)f[++c]=-(X[a][i]/CC*CC+t-Y[a][i]);
    for(int i=0;i<X[b].size();++i)f[++c]=X[b][i]/CC*CC+t-Y[b][i]+C;
    sort(f+1,f+1+c);
    nC1=floor(f[c+1>>1]*1./C)*C;nC2=ceil(f[c+1>>1]*1./C)*C;
    for(int i=1;i<=c;++i)f1+=abs(f[i]-nC1),f2+=abs(f[i]-nC2);
    return min(f1,f2);
}
int main(){
    cin>>C>>n>>_x>>xa>>xb>>xp>>_y>>ya>>yb>>yp; CC=C+C;
    for(int i=0;i<n;++i)X[_x%CC].push_back(_x),Y[_x%CC].push_back(_y),_x=(1ll*_x*xa+xb)%xp,_y=(1ll*_y*ya+yb)%yp;
    for(int i=0;i<CC;i+=2)for(int j=1;j<CC;j+=2)con(i,j,cal(i,j));
    for(int i=0;i<CC;++i)if(i&1)con(i,CC+1,0);else con(CC,i,0);
    while(bfs())dfs(CC,C); cout<<ans;
}