[考试反思]0313省选模拟44:习惯
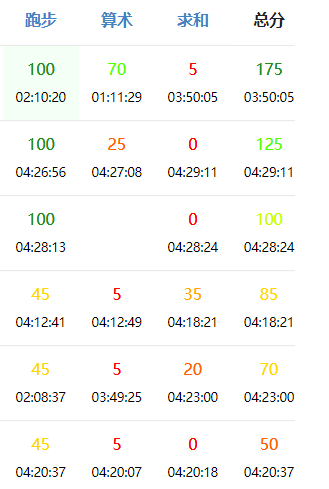

我也不知道我在干什么了。侥幸还是害人啊。
$T1$一个变量名的大小写写错了(Shift没按住)然后就爆零了,丢了$45$分。
然后$OJ$貌似终于支持静态内存了?
不知道反正我就谜之$MLE$了,我根本都没用那东西。然后开小点就有$35$分了。
$85$分的场打成$5$分。哎。。。。。
话说这套题好恶心啊,部分分很少且没有什么用,想不到正解基本就没什么分。
(我就想说:所有最后一档部分分大于50的题的出题人脑子都有问题!)
于是考着就挺难受的,下次还是要多动脑子想正解,仨暴力真的没什么分。。。
T1:跑步
大意:$n \times n$矩阵,$n$次修改。每个点有权值,定义每个点的贡献为它向上或左走到$(1,1)$经过的点权和的最大值。每次修改后,求所有点的贡献和。$n \le 2000$
可以发现每次修改影响的,对于每一行若是$[l_i,r_i]$的话,那么有对于任意$i<j$有$l_i \le l_j,r_i \le r_j$
那么直接差分,树状数组维护,然后单调指针扫,总复杂度是$O((n+q)nlogn)$的。

1 #include<bits/stdc++.h> 2 using namespace std; 3 int a[2222][2222],n,dp[2222][2222],t[2222][2222];char s[5];long long ans; 4 void add(int o,int p,int w){for(;p<=n;p+=p&-p)t[o][p]+=w;} 5 int ask(int o,int p,int w=0){for(;p;p^=p&-p)w+=t[o][p];return w;} 6 int main(){ 7 scanf("%d",&n); 8 for(int i=1;i<=n;++i)for(int j=1;j<=n;++j) 9 scanf("%d",&a[i][j]),dp[i][j]=max(dp[i-1][j],dp[i][j-1])+a[i][j],ans+=dp[i][j],add(i,j,dp[i][j]-dp[i][j-1]); 10 for(int i=1;i<=n;++i)t[i][n+1]=1e9; 11 printf("%lld\n",ans); 12 for(int q=1,x,y,v;q<=n;++q){ 13 scanf("%s%d%d",s,&x,&y); 14 v=s[0]=='U'?1:-1;a[x][y]+=v; 15 int l=y,r=y; 16 for(int i=x;i<=n;++i){ 17 while(ask(i,l)==max(ask(i-1,l),ask(i,l-1))+a[i][l]&&l<=n)l++; 18 add(i,l,v);add(i,r+1,-v);ans+=v*(r-l+1); 19 while(ask(i,r+1)!=max(ask(i-1,r+1),ask(i,r))+a[i][r+1]&&r<n)r++,add(i,r,v),add(i,r+1,-v),ans+=v; 20 }printf("%lld\n",ans); 21 } 22 }
T2:算术
大意:多测,问$\sqrt[k]{n}$是不是整数。$n \le 10^{1000000},k \le 10^7$
其实挺不靠谱的一道题。
数太大于是随机一个质数去取模。开跟的话感觉像$k$次剩余?
我们对于一个质数$p$,有$x^{p-1} \equiv 1 (mod \ p)$
而如果$p$可以表示成$ak+1$那么就是说$x^{ak} \equiv 1(mod \ p)$
那么就有$(n \ mod p)^{a} \equiv 1(mod \ p)$。也就相当于模意义下开跟了。
多枚举几个$a$进行判断就是了,正确率很高。

1 #include<bits/stdc++.h> 2 using namespace std; 3 char n[1000005]; 4 bool prime(int x){for(int i=2;i*i<=x;++i)if(x%i==0)return 0;return 1;} 5 bool chk(int b,int t,int mod,int a=1){for(;t;t>>=1,b=1ll*b*b%mod)if(t&1)a=1ll*a*b%mod;return a>1;} 6 int main(){ 7 int t;cin>>t;while(t--){ 8 int k,p,N,s;scanf("%s%d",n,&k); 9 for(int a=1;a<=20;++a)if(prime(p=a*k+1)){ 10 N=0;for(int i=0;n[i];++i)N=(N*10ll+n[i]-'0')%p; 11 if(chk(N,a,p))goto no; 12 }puts("Y");continue;no:puts("N"); 13 } 14 }
T3:求和
大意:数列,支持单点修改,每次之后查询$\max\limits_{|i-j| \le k} a_i+a_j$。$n,q \le 10^6$
大概意思就是说,答案一定会出现在满足$j\in [i-k,i+k],a_j \le a_i$的$i$上。
所以每次修改的时候,这样的位置的数量只有修改点,修改点左侧$k$以内的最大值,修改点右侧$k$以内的最大值这三个位置。
然后就需要一棵维护区间最值单点修改的线段树,据说此题毒瘤卡常得用$zkw$才能通过。
然后再开一颗线段树,维护每个下标贡献的答案值,单点修改查询全局$max$。
代码先咕着吧。
然而实际上,讲道理来说,如果你真的对于某个特定点去找两侧的最值的话,你应该找离中心最远的。
那么你在权值相同时到底应该维护坐标最大值还是最小值呢?很麻烦。
所以我们稍微改一下,不再要求两边都小于等于当前值就更新答案,而是左边小于等于,右边大于的点就好了。
因为等于号有传递性,所以依旧能考虑到所有情况,这样的话你就只需要维护权值相等时的最大值就好了。

1 #include<bits/stdc++.h> 2 using namespace std; 3 int read(){ 4 register char ch=getchar();register int p=0; 5 while(ch<'0'||ch>'9')ch=getchar(); 6 while(isdigit(ch))p=p*10+ch-48,ch=getchar(); 7 return p; 8 } 9 #define S 3000005 10 int n,a[S],pos[S],v[S],k,q,op,bin=1; 11 int cmp(int x,int y){return a[x]>a[y]?x:(a[x]==a[y]?max(x,y):y);} 12 void chg(int p,int w){for(v[p+=bin]=w;p^1;p>>=1)v[p>>1]=max(v[p],v[p^1]);} 13 void upd(int p){for(p=p+bin;p>>=1;)pos[p]=cmp(pos[p<<1],pos[p<<1|1]);} 14 int ask(int l,int r,int a=0){ 15 for(l+=bin-1,r+=bin+1;l^r^1;l>>=1,r>>=1){ 16 if(l&1^1)a=cmp(a,pos[l^1]); 17 if(r&1)a=cmp(a,pos[r^1]); 18 }return a; 19 } 20 int main(){ 21 cin>>n>>k>>q>>op; a[0]=-1; a[n+1]=0x7fffffff; 22 while(bin<=n)bin<<=1; 23 for(int i=1;i<=n;++i)a[i]=v[i+bin]=read(),pos[i+bin]=i; 24 for(int i=bin-1;i;--i)v[i]=max(v[i<<1],v[i<<1|1]),pos[i]=cmp(pos[i<<1],pos[i<<1|1]); 25 for(int i=1,x,y;i<=n;++i){ 26 x=ask(max(1,i-k),i-1),y=ask(i+1,min(n,i+k)); 27 if(a[x]<=a[i]&&a[y]<a[i])chg(i,a[i]+max(a[x],a[y])); 28 }printf("%d\n",v[1]); 29 while(q--){ 30 int x=read(),y=read(),z,xx,yy; if(op)x^=v[1],y^=v[1]; a[x]=y; upd(x); 31 y=ask(max(1,x-k),x-1);z=ask(x+1,min(x+k,n)); 32 if(a[y]<=a[x]&&a[z]<a[x])chg(x,a[x]+max(a[z],a[y])); 33 else{ 34 if(v[x+bin]>0)chg(x,0); 35 xx=y?ask(max(y-k,1),y-1):n+1; yy=a[xx]<=a[y]?ask(y+1,min(y+k,n)):n+1; 36 if(a[yy]<a[y])chg(y,a[y]+max(a[yy],a[xx])); 37 xx=z?ask(max(z-k,1),z-1):n+1; yy=a[xx]<=a[z]?ask(z+1,min(z+k,n)):n+1; 38 if(a[yy]<a[z])chg(z,a[z]+max(a[yy],a[xx])); 39 }printf("%d\n",v[1]); 40 } 41 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号