[考试反思]0310省选模拟42:清醒
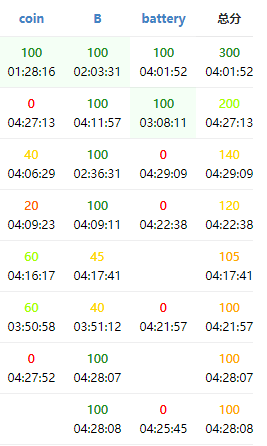

网卡电脑卡鼠标卡,最后一分钟$T2$又没交上去,丢了$35$分。
T1无良出题人卡精。和$std$不一样差不多都会卡。写暴力没$T$反而$WA$了。
然后写$FFT$想优化复杂度结果精炸的更厉害了,暴力卷积反而有$70$分。
难度评估错误,刚$T1$上了。
一眼看出$T3$不是网络流就是$2sat$然后没有继续想下去。
$T2$上来一道原题直接扔掉,后来又换题,还是原题但是没看出来(?)
刷题是挺快,白刷了都?脑子呢?不知道。
也就$T1$会点乱搞,如果不卡精应该能$80,100$那样。
还是不好,差距还是很大。。。
加把劲啊!!!!
T1:coin
大意:$n$个人,$m$个礼物,每个人喜欢其中恰好一种。$i$喜欢礼物$j$的概率是$p_{i,j}$。你可以带$n$件礼物回来。最多期望让多少人得到喜欢的礼物。$n \le 3000,m\le 300$
不难发现,设你带某种礼物$x$件的贡献是$f(x)$那么有$f(x+2)-f(x+1) \le f(x+1)-f(x)$
那么就是说每多一件礼物,收益是递减的。
所以开一个堆,维护$(i,j,w)$表示第$i$种礼物选第$j$份的收益是$w$。贪心的选最大的就好了。
问题在于求出$w$。设$f(k,c,n)$表示对于前$n$个人第$k$种礼物一共有$c$份的贡献。$w=f(i,j,n)-f(i,j-1,n)$
然后$f$可以直接记忆化搜索求解。看起来转移式子递归了两边但是实际上有一边在把$i,j-1,v)$扔进堆里时已经计算出来了。
总复杂度$O(n^2+nm+mlogn)$

1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,m,P[3333][333],al[3333];double p[3333][333],ans; 4 priority_queue<pair<double,int> >q;vector<double>M[303][3003]; 5 double f(int k,int c,int n){ 6 while(!P[n][k]&&n)n--; 7 if(c==0||!n)return 0; 8 if(M[k][c][n])return M[k][c][n]; 9 return M[k][c][n]=(1+f(k,c-1,n-1))*p[n][k]+f(k,c,n-1)*(1-p[n][k]); 10 } 11 int main(){ 12 cin>>n>>m; 13 for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)scanf("%d",&P[i][j]),p[i][j]=P[i][j]/1000.; 14 for(int i=1;i<=m;++i)M[i][0].resize(n+1),M[i][1].resize(n+1),q.push(make_pair(f(i,1,n),i)); 15 for(int i=1;i<=n;++i){ 16 ans+=q.top().first;int k=q.top().second;q.pop(); 17 al[k]++;M[k][al[k]+1].resize(n+1);q.push(make_pair(f(k,al[k]+1,n)-f(k,al[k],n),k)); 18 }printf("%.10lf\n",ans); 19 }
T2:B
大意:树,断开$k$条边再任意连边,最后能形成几种树。$k \le n \le 50$
要求的是有多少边是原树上的边。然后就是原题了。
https://www.cnblogs.com/hzoi-DeepinC/p/12257630.html

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define mod 998244353 4 int al[55][55],n,k,M[55][55],A[55][55],ans; 5 int qp(int b,int t,int a=1){for(;t;t>>=1,b=1ll*b*b%mod)if(t&1)a=1ll*a*b%mod;return a;} 6 void Gauss(){ 7 for(int i=1;i<=n;++i){ 8 int iv=qp(A[i][i],mod-2); 9 for(int j=i;j<=1+n;++j)A[i][j]=1ll*A[i][j]*iv%mod; 10 for(int j=1;j<=n;++j)if(i!=j)for(int k=n+1;k>=i;--k)A[j][k]=(A[j][k]+mod-1ll*A[j][i]*A[i][k]%mod)%mod; 11 } 12 } 13 int MT(int a=1){ 14 for(int i=1;i<n;++i){ 15 int iv=qp(M[i][i],mod-2);a=1ll*a*M[i][i]%mod; 16 for(int j=i;j<n;++j)M[i][j]=1ll*M[i][j]*iv%mod; 17 for(int j=i+1;j<n;++j)for(int k=n-1;k>=i;--k)M[j][k]=(M[j][k]+mod-1ll*M[j][i]*M[i][k]%mod)%mod; 18 }return a; 19 } 20 int main(){ 21 scanf("%d%d",&n,&k); 22 for(int i=2,f;i<=n;++i)cin>>f,al[i][f+1]=al[f+1][i]=1; 23 for(int I=1;I<=n;++I){ 24 for(int i=1;i<=n;++i)for(int j=1;j<=n;++j)M[i][j]=0; 25 for(int i=1;i<=n;++i)for(int j=1;j<i;++j) 26 if(al[i][j])M[i][j]=mod-1,M[j][i]=mod-1,M[i][i]++,M[j][j]++; 27 else M[i][j]=mod-I,M[j][i]=mod-I,M[i][i]+=I,M[j][j]+=I; 28 A[I][1]=1; 29 for(int i=2;i<=n;++i)A[I][i]=1ll*A[I][i-1]*I%mod; 30 A[I][n+1]=MT(); 31 }Gauss(); 32 for(int i=1;i<=k+1;++i)ans=(ans+A[i][n+1])%mod; 33 cout<<ans<<endl; 34 }
T3:battery
大意:网格,每个格子上有炮台向上下或向左右发射激光,有左上右下,左下右上两种反射镜,以及吸收激光的障碍物,以及空格。
求一种炮台射向方案满足任何激光不打到炮台且所有空格都被打到。$n,m \le 50 ,T \le 100$
对于不能打到其它炮台,首先$DFS$求出每个炮台允许的朝向。
然后对于每个空格,它最多只会被两个炮台打到。如果来源方向相同那么两个炮台会互相打到,所以只有左右,上下两个可能方向。
如果这个空格没有炮台能打到,那么无解。
如果只有一个炮台的某个特定朝向能打到,那么将这个炮台定向。
如果是两个,那么$A$炮台不采取对应朝向的话$B$就必须采取,$B$对$A$同理。
经典的$2sat$问题。只有“必须选某个点”和“选A就必须选B”两种限制。
所以直接来就好了。如果没有把地图周围加障碍的话字符串可能需要多测清空。

1 #include<bits/stdc++.h> 2 using namespace std; 3 char s[55][55]; 4 int n,m,cnt,rx[5555],ry[5555],ok,ob[55][55],bc,bl[5555]; 5 const int dx[]={1,-1,0,0},dy[]={0,0,1,-1}; 6 int fir[5555],l[9999],to[9999],ec,dfn[5555],scc,tim,low[5555],sta[5555],ins[5555],top; 7 vector<int>cr,by[2555]; 8 void link(int a,int b){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;} 9 void dfs(int x,int y,int d){ 10 if(s[x][y]=='#'||!ok)return; 11 if(s[x][y]=='.')cr.push_back(ob[x][y]),dfs(x+dx[d],y+dy[d],d); 12 if(s[x][y]=='-')return void(ok=0); 13 if(s[x][y]=='/')dfs(x+dx[3-d],y+dy[3-d],3-d); 14 if(s[x][y]=='\\')dfs(x+dx[3-d^1],y+dy[3-d^1],3-d^1); 15 } 16 void tarjan(int p){ 17 dfn[p]=low[p]=++tim;sta[++top]=p;ins[p]=1; 18 for(int i=fir[p];i;i=l[i])if(!dfn[to[i]])tarjan(to[i]),low[p]=min(low[p],low[to[i]]); 19 else if(ins[to[i]])low[p]=min(low[p],dfn[to[i]]); 20 if(dfn[p]==low[p]){ 21 scc++; 22 while(ins[p])bl[sta[top]]=scc,ins[sta[top]]=0,top--; 23 } 24 } 25 int main(){int T;cin>>T;while(T--){ 26 cin>>n>>m; 27 for(int i=2;i<=cnt;++i)fir[i]=dfn[i]=0; 28 for(int i=1;i<=m;++i)s[n+1][i]=0; 29 cnt=1;bc=tim=ec=scc=0; 30 for(int i=1;i<=n;++i)cin>>s[i]+1; 31 for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)if(s[i][j]=='|')s[i][j]='-'; 32 for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)if(s[i][j]=='.')ob[i][j]=++bc,by[bc].clear(); 33 for(int i=1;i<=n;++i)for(int j=1,r;j<=m;++j)if(s[i][j]=='-'){ 34 ok=1;dfs(i-1,j,1);dfs(i+1,j,0);r=ok;rx[++cnt]=i,ry[cnt]=j; 35 if(ok)for(int x=0;x<cr.size();++x)by[cr[x]].push_back(cnt);cr.clear(); 36 ok=1;dfs(i,j-1,3);dfs(i,j+1,2);++cnt; 37 if(ok)for(int x=0;x<cr.size();++x)by[cr[x]].push_back(cnt);cr.clear(); 38 if(!r&&!ok)goto fail; 39 if(!r)link(cnt-1,cnt); 40 if(!ok)link(cnt,cnt-1); 41 } 42 for(int i=1;i<=bc;++i)if(!by[i].size())goto fail; 43 else if(by[i].size()==1)link(by[i][0]^1,by[i][0]); 44 else link(by[i][1]^1,by[i][0]),link(by[i][0]^1,by[i][1]); 45 for(int i=2;i<=cnt;++i)if(!dfn[i])tarjan(i); 46 for(int i=2;i<=cnt;i+=2)if(bl[i]==bl[i^1])goto fail; 47 for(int i=2;i<=cnt;i+=2)s[rx[i]][ry[i]]=bl[i]>bl[i^1]?'-':'|'; 48 puts("POSSIBLE"); 49 for(int i=1;i<=n;++i,puts(""))for(int j=1;j<=m;++j)putchar(s[i][j]); 50 continue;fail:puts("IMPOSSIBLE"); 51 }}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号