2024.2.6鲜花

推歌

《以恋结缘》

诚、意地の悪い神の所业か？

奇迹？縁？袂触合う不思议

花ひとひら揺れて

不意に宿ってた

うなじ解いてく春风

戯れはそこそこに

恋手ほどきしてくだしゃんせ

汤気にほんのり頬染て

夜风に愿ふ

…いざ！！蝶と舞ひ花となりて

衣を乱して祓いましょう

あやなしココロの秽れ

…故！！刀となり楯となりて

この想ひ护り赐え

君が恋の门を杀めた

恋の罠は密やかに仕挂けなきゃ

次の一手すけすけだから困る

锻錬じゃどうにもなんない

揺れる心模様

どっちが先だ？恋烦ひ

覚悟してとおりゃんせ

夜道と乙女にご用心

汤気の香り漂わせ诱う夜宴

…実に！本日はデェト日和

しどけなく诱いましょ？

凭きませ偲ぶ恋梦…

故！静となり动となりて

我を导き赐え

君の剣がハァトを射抜いた

…いざ！！蝶と舞ひ花となりて

衣を乱して祓いましょう

前世から繋がる运命

…故！刀となり花と生きて

この爱护り赐え

君はもう縁に选ばれた

用来求方程近似解的。前置知识是导数，然后没了。

大致就是先随机一个近似解 \(x_0\)（只要别太离谱就行），然后求 \(f(x)\) 在 \(x=x_0\) 处的切线 \(g(x)\)，再以 \(g(x)\) 和 \(x\) 轴的交点 \(x_1\)作为近似解，直到 \(f(x_{n})\) 接近 0。

画个图，\(f(x)=\frac{1}{15}x^{3}-\frac{1}{5}x^{2}-1\)，就是红色那条线，\(x_0=6\)：

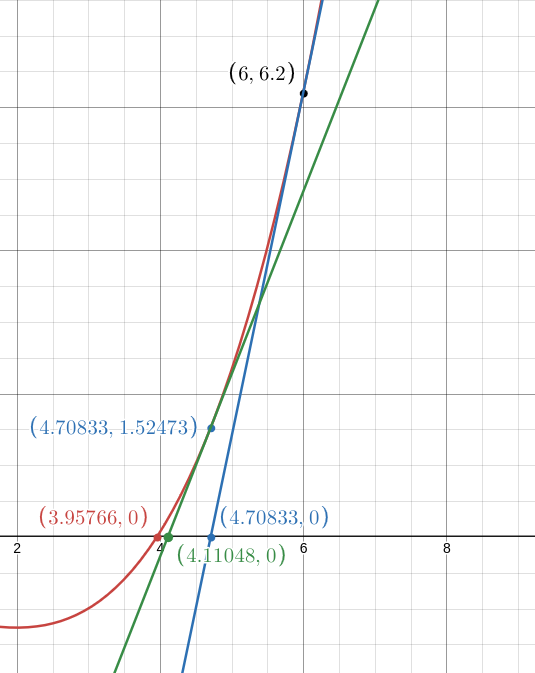
可以看到收敛速度还是很快的（反正比隔壁二分快）。有人证明了这玩意的收敛率是平方级别的，详见citizendium - Newton method Convergence analysis（学校没开网不知道能不能打开，如果链接挂了，那就挂了吧）。

高数上也有讲这玩意的，但不是叫做牛顿迭代了，叫切线法。大概就是说如果 \(f(x)\) 在 \([a,b]\) 上有二阶导数， \(f(a)\cdot f(b)<0\) 且 \(f^\prime(x),f^{\prime\prime}(x)\) 定号，那么就有 \(f(x)=0\) 在 \((a,b)\) 内有唯一根，然后就迭代求解。

不难看出 \(x_{i+1}=x_i-\frac{f(x_i)}{f^\prime(x_i)}\)。用这个东西手写一个 sqrt。

code

db Sqrt(db n){
  db x = 1;
  auto f = [&](db x){return x*x-n;};
  auto fd = [&](db x){return 2*x;};
  while(fabs(f(x)) > 1e-6) x = x-f(x)/fd(x);
  return x;
}

牛顿迭代是有缺陷的，有浮点数无法避免的误差，还有如果两个迭代点相距较远，可能会导致迭代过程发散或者收敛速度变慢。

有个优化叫牛顿爬山法，为了保证每次迭代后 \(|f(x_{i+1})|<|f(x_i)|\)，设一个爬山因子 \(\lambda\)，做加权平均，取 \(0<\lambda\le 1\)，一般 \(\lambda\) 依次取 \(1,\frac{1}{2},\frac{1}{4},\cdots\)。

那显然我们不可能只是用这么高级的东西求一个方程的解吧。还可以把这玩意扔到多项式上，我还没学，先咕着。

一篇关于牛顿迭代初值如何选取的博客

p