FFT+NTT入门
真的只是入门。
可能还会更新 分治FFT 或者 任意模数NTT?
前置知识
复数 也可以参考高中数学课本,这里只会介绍 fft 需要的(默认已经入门复数)。
点值表示法:假设 \(f(x)\) 是一个 \(n-1\) 次多项式,那么将 \(n\) 个 不同的 \(x\) 代入,可以得到 \(n\) 个 \(y\)。这 \(n\) 个点对 \((x,y)\) 唯一确定了该多项式。那么就可以通过多项式求出其点值表示,也可以反过来。
注意:以下 \(n\) 均为 \(2\) 的整数次幂,若不足则补零(显然不会影响结果)
FFT 简介
用来加速多项式乘法的一个东西。而普通多项式乘法是 \(O(n^2)\) 的。但是如果是点值表示法,则是 \(O(n)\) 的(比如 \(c(x) = a(x)\times b(x)\),那么只需要枚举 \(2\times n\) 个不同的 \(x\) 即可求出 \(c\) 的点值表示)。
考虑如何快速将两个多项式 \(a(x),b(x)\) 转成点值表示,再将一个多项式 \(c(x)\) 从点值表示转化回来即可。
这里就用到 FFT 了。
离散傅里叶变换
其实就是朴素版 FFT。
就是上面代入的 \(n\) 个 \(x\) 为 \(n\) 个复数。但这 \(n\) 个复数不是随便找的,而是 \(n\) 次单位根。
简单介绍一下,就是 \(x^n=1\) 在复数意义下所有的根。显然这玩意有 \(n\) 个。将这几个根按幅角从小到大排序,从 \(0\) 开始编号,第 \(i\) 个 \(n\) 次单位根记为 \(w_n^i\)。没有特殊声明时,一般特指第一个单位根,简记为 \(w_n\)。
可以算出 \(w_n^k=\cos(\frac{2k\pi}{n})+i\sin(\frac{2k\pi}{n})\)。
有两个性质:
- \(w_{2n}^{2k}=w_n^k\)。画个图理解一下。
- \(w_{n}^{k+\frac{n}{2}}-w_{n}^{k}\),画图发现它们关于原点对称。
画个图出来,大概这样子。
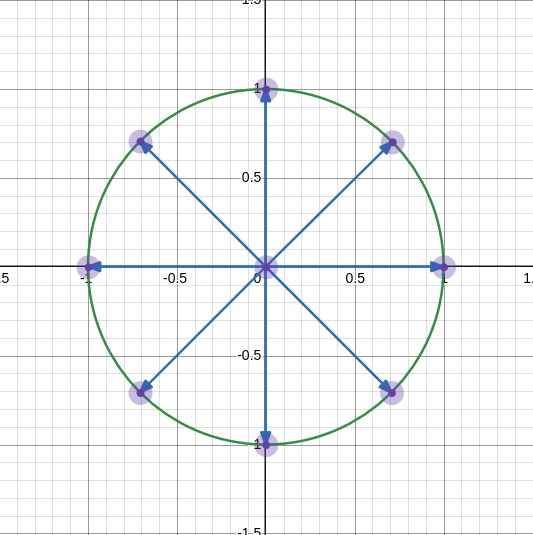
好看是好看, 但是为什么非要选择这 \(n\) 个点呢?
有个结论,将 \(a(x)\) 的离散傅里叶变换的结果作为 \(b(x)\) 的系数,将单位根的倒数 \(w_n^0,w_n^{-1},w_n^{-2},\cdots,w_n^{-n+1}\) 代入以后,得到的每个数再除以 \(n\),就是 \(a(x)\) 的各项系数。
证明
设 \((b_0,b_1,\cdots,b_{n-1})\) 为 \(A(x)=a_0+a_1x+a_2x^2+\cdots+a_nx^{n-1}\) 离散傅里叶变换的结果。
设 \(B(x) = b_0+b_1x+\cdots+b_nx^{n-1}\),然后将那几个单位根的倒数代入得到一个新的离散傅里叶变换结果 \((c_0,c_1,\cdots,c_{n-1})\)。
有
发现当且仅当 \(j=k\) 时,后面式子的值为 \(n\),反之,后面的式子值为 \(0\)。
那么就有了 \(a_i=\frac{c_i}{n}\)。
然后这样就是 \(O(n^2)\) 的了,没啥用啊。
这是因为傅里叶爷爷 (1768年3月21日~1830年5月16日) 没有见过计算机(世界上第一台通用计算机“ENIAC”于1946年2月14日在美国宾夕法尼亚大学诞生),所以他不需要考虑时间复杂度,但是后人就要优化了。
考虑一个多项式 \(A(x)=a_0+a_1x+a_2x^2+\cdots+a^{n-1}x^{n-1}\) 要求离散傅里叶变换,将一个 \(w_n\) 代入。
将 \(A(x)\) 的每一项按照下标奇偶性分组,设 \(A_1(x)=a_0+a_2x+\cdots+a^{n-2}x^{\frac{n}{2}-1},A_2(x) = a_1 + a_3x + \cdots + a_{n - 1}x^{\frac{n}{2} - 1}\)。
显然有 \(A(x) = A_1(x^2)+xA_2(x^2)\)。
将 \(w_n^k(k<\frac{n}{2})\) 代入,有 \(A(w_n^k)=A_1(w_n^{2k})+w_n^kA_2(w_n^{2k})=A_1(w_{\frac{n}{2}}^k)+w_{n}^kA_2(w_{\frac{n}{2}}^k)\)。
那么将 \(w_n^{k+\frac{n}{2}}\) 代入,最后得到一个 \(A_1(w_n^{2k})-w_n^kA_2(w_n^{2k})\)。
发现这两个式子只有一个常数项不同,那么求第一个式子可以顺便将第二个式子求出来,因为第一个式子取遍 \([0,\frac{n}{2}-1]\),第二个式子取遍 \([\frac{n}{2},n]\),所以将原问题缩小了一半,而且缩小后的问题符合原问题性质,然后就这么递归分治下去即可。
时间复杂度 \(O(n\log n)\)。
递归实现,跑的好像不是很慢。
个人感觉递归实现便于理解,可以先打递归实现试试水。
code
#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t;i += p)
#define drep(i,s,t,p) for(int i = s;i >= t;i -= p)
#ifdef LOCAL
auto I = freopen("in.in","r",stdin),O = freopen("out.out","w",stdout);
#else
auto I = stdin,O = stdout;
#endif
using ll = long long;using ull = unsigned long long;
using db = double;using ldb = long double;
using comp = complex<db>;
const db pi = acos(-1);
const int N = 4e6 + 10;
int n,m;comp a[N],b[N];
void fft(comp *a,int n,int inv){
if(n == 1) return;//最后了,直接 return 就好啦。
int m = n>>1;
comp a1[m+5],a2[m+5];
rep(i,0,n,2) a1[i>>1] = a[i],a2[i>>1] = a[i+1];//奇偶分组
fft(a1,m,inv);fft(a2,m,inv);
comp W = comp(cos(2.0*pi/n),inv*sin(2.0*pi/n)),w = comp(1,0);//单位根。
for(int i = 0;i < m;++i,w = w*W){
a[i] = a1[i] + w*a2[i];//求A1。
a[i+m] = a1[i] - w*a2[i];//求A2。
}
}
signed main(){
cin.tie(nullptr)->sync_with_stdio(false);
cin>>n>>m;
rep(i,0,n,1) cin>>a[i];
rep(i,0,m,1) cin>>b[i];
int lim = 1;while(lim <= n+m) lim <<= 1;//凑成 2^n
fft(a,lim,1);fft(b,lim,1);//转成点值表示
rep(i,0,lim,1) a[i] = a[i]*b[i];//点值乘
fft(a,lim,-1);//转成系数表示
rep(i,0,n+m,1) cout<<(int)(a[i].real()/lim+0.5)<<' ';
}
但是相比于常写的迭代写法来说,这种写法还是比较慢。(在洛谷这道题,最后一个数据点,递归跑了 1000ms,迭代跑了 600多ms)
那么如何写成迭代法呢?
考虑最后进行操作的序列,发现其实最后操作的序列就是将下标二进制位翻转排序。
手动模拟一下应该很好理解,就是先以二进制位下第零位奇偶分组,然后每组中以第一位奇偶分组,以此类推。
那么就可以知道每个数最后应该在的位置,这个可以递推出来,假如当前位置为 \(i\),那么它会在 (to[i>>1]>>1)|((i&1)<<(ct-1)),其中 \(to_i\) 表示第 \(i\) 个数应该在的位置,显然有 i=to[to[i]],\(ct\) 是二进制位数,即 \(n=2^{ct}\)。
然后就可以递推出结果了。
code
#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t;i += p)
#define drep(i,s,t,p) for(int i = s;i >= t;i -= p)
#ifdef LOCAL
auto I = freopen("in.in","r",stdin),O = freopen("out.out","w",stdout);
#else
auto I = stdin,O = stdout;
#endif
using ll = long long;using ull = unsigned long long;
using db = double;using ldb = long double;
using comp = complex<db>;
const int N = 4e6 + 10;
const db pi = acos(-1);
int n,m,to[N],ct;
comp a[N],b[N];
void fft(comp *a,int n,int type){
rep(i,0,n-1,1) if(i < to[i]) swap(a[i],a[to[i]]);
for(int mid = 1;mid < n;mid <<= 1){
comp W = comp(cos(pi/mid),type*sin(pi/mid));
for(int Res = mid<<1,j = 0;j < n;j += Res){
comp w = comp(1,0);
for(int k = 0;k < mid; ++k,w = w*W){
comp x = a[j+k],y = w*a[j+mid+k];
a[j+k] = x + y;
a[j+mid+k] = x-y;
}
}
}
}
signed main(){
cin.tie(nullptr)->sync_with_stdio(false);
cin>>n>>m;rep(i,0,n,1) cin>>a[i];rep(i,0,m,1) cin>>b[i];
int lim = 1;while(lim <= (n+m)) lim <<= 1,ct++;
rep(i,0,lim-1,1) to[i] = (to[i>>1]>>1)|((i&1)<<(ct-1));
fft(a,lim,1);fft(b,lim,1);
rep(i,0,lim,1) a[i] = a[i]*b[i];
fft(a,lim,-1);
rep(i,0,n+m,1) cout<<(int)(a[i].real()/lim+0.5)<<' ';
}
实际应用中还可以预处理单位根,但我写丑了,跑的还没不预处理的快(甚至不如递归)
code
#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t;i += p)
#define drep(i,s,t,p) for(int i = s;i >= t;i -= p)
#ifdef LOCAL
auto I = freopen("in.in","r",stdin),O = freopen("out.out","w",stdout);
#else
auto I = stdin,O = stdout;
#endif
using ll = long long;using ull = unsigned long long;
using db = double;using ldb = long double;
using comp = complex<db>;
const int N = 4e6 + 10;
const db pi = acos(-1);
int n,m,to[N],ct;
comp a[N],b[N],urt[N],iurt[N];
void fft(comp *a,comp *urt,int n){
rep(i,0,n-1,1) if(i < to[i]) swap(a[i],a[to[i]]);
for(int mid = 1;mid < n;mid <<= 1){
for(int Res = mid<<1,j = 0;j < n;j += Res){
for(int k = 0;k < mid; ++k){
comp x = a[j+k],y = urt[n/mid*k]*a[j+mid+k];
a[j+k] = x + y;
a[j+mid+k] = x-y;
}
}
}
}
signed main(){
cin.tie(nullptr)->sync_with_stdio(false);
cin>>n>>m;rep(i,0,n,1) cin>>a[i];rep(i,0,m,1) cin>>b[i];
int lim = 1;while(lim <= (n+m)) lim <<= 1,ct++;
comp W = comp(cos(pi/lim),sin(pi/lim));
urt[0] = comp(1,0);rep(i,1,lim,1) urt[i] = urt[i-1]*W;
W = conj(W);iurt[0] = comp(1,0);
rep(i,1,lim,1) iurt[i] = iurt[i-1]*W;
rep(i,0,lim-1,1) to[i] = (to[i>>1]>>1)|((i&1)<<(ct-1));
fft(a,urt,lim);fft(b,urt,lim);
rep(i,0,lim,1) a[i] = a[i]*b[i];
fft(a,iurt,lim);
rep(i,0,n+m,1) cout<<(int)(a[i].real()/lim+0.5)<<' ';
}
奇技淫巧:三次变两次。
考虑 \((a+bi)\times (c+di) = (ac-bd)+(bc+ad)i\)。
假设要求 \(f(x)*g(x)\)。
设 \(h(x) = f(x)+g(x)i\),那么 \(h^2(x)=f^2(x)-g^2(x)+2f(x)g(x)i\)。
所以卷出 \(h^2\) ,其虚部除以二即可。
但是两个多项式值域相差太大,会有精度问题。
稍稍卡了卡常,手写了个复数类,比我写的不卡常 NTT 快一点。
code
#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t;i += p)
#define drep(i,s,t,p) for(int i = s;i >= t;i -= p)
#ifdef LOCAL
auto I = freopen("in.in","r",stdin),O = freopen("out.out","w",stdout);
#else
auto I = stdin,O = stdout;
#endif
using ll = long long;using ull = unsigned long long;
using db = double;using ldb = long double;
const int N = 4e6 + 10;
const db pi = acos(-1);
int n,m,to[N],ct;
struct comp{
db x,y;comp(){}
comp(db X,db Y){x = X,y = Y;}
comp operator + (const comp& a){return comp(x+a.x,y+a.y);}
comp operator - (const comp& a){return comp(x-a.x,y-a.y);}
comp operator * (const comp& a){return comp(x*a.x-y*a.y,y*a.x+x*a.y);}
db real(){return x;}
db imag(){return y;}
}a[N];
void fft(comp *a,int n,int type){
rep(i,0,n-1,1) if(i < to[i]) swap(a[i],a[to[i]]);
for(int mid = 1;mid < n;mid <<= 1){
comp W = comp(cos(pi/mid),type*sin(pi/mid));
for(int Res = mid<<1,j = 0;j < n;j += Res){
comp w = comp(1,0);
for(int k = 0;k < mid; ++k,w = w*W){
comp x = a[j+k],y = w*a[j+mid+k];
a[j+k] = x + y;
a[j+mid+k] = x - y;
}
}
}
}
signed main(){
cin.tie(nullptr)->sync_with_stdio(false);
cin>>n>>m;rep(i,0,n,1) cin>>a[i].x;rep(i,0,m,1) cin>>a[i].y;
int lim = 1;while(lim <= (n+m)) lim <<= 1,ct++;
rep(i,0,lim-1,1) to[i] = (to[i>>1]>>1)|((i&1)<<(ct-1));
fft(a,lim,1);
rep(i,0,lim,1) a[i] = a[i]*a[i];
fft(a,lim,-1);
rep(i,0,n+m,1) cout<<(int)(a[i].imag()/lim/2+0.5)<<' ';
}
例题:【模板】高精度乘法 | A*B Problem 升级版
没有压位,和高精一样写即可,就是乘法由暴力乘换成了 fft。
code
#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t;i += p)
#define drep(i,s,t,p) for(int i = s;i >= t;i -= p)
#ifdef LOCAL
auto I = freopen("in.in","r",stdin),O = freopen("out.out","w",stdout);
#else
auto I = stdin,O = stdout;
#endif
using ll = long long;using ull = unsigned long long;
using db = double;using ldb = long double;
using comp = complex<db>;
const db pi = acos(-1);
const int N = 4e6 + 10;
string s1,s2;
int n,m,ct,to[N],ans[N];comp a[N],b[N];
void fft(comp *a,int type,int n){
rep(i,0,n,1) if(i < to[i]) swap(a[i],a[to[i]]);
for(int mid = 1;mid < n;mid <<= 1){
comp W = comp(cos(pi/mid),type*sin(pi/mid));
for(int Res = mid<<1,j = 0;j < n;j += Res){
comp w = comp(1,0);
for(int k = 0;k < mid; ++k,w = w*W){
auto x = a[j+k],y = w*a[j+mid+k];
a[j+k] = x+y;
a[j+mid+k] = x-y;
}
}
}
}
signed main(){
cin.tie(nullptr)->sync_with_stdio(false);
cin>>s1>>s2;n = s1.size() - 1,m = s2.size() - 1;
reverse(s1.begin(),s1.end());
reverse(s2.begin(),s2.end());
rep(i,0,n,1) a[i] = comp(s1[i]-'0',0);
rep(i,0,m,1) b[i] = comp(s2[i]-'0',0);
int lim = 1;while(lim <= (n+m)) lim <<= 1,ct++;
rep(i,0,lim,1) to[i] = (to[i>>1]>>1)|((i&1)<<(ct-1));
fft(a,1,lim);fft(b,1,lim);
rep(i,0,lim,1) a[i] = a[i]*b[i];
fft(a,-1,lim);
rep(i,0,lim,1) ans[i] = (int)(a[i].real()/lim+0.5);
rep(i,0,lim,1) ans[i+1] += ans[i]/10,ans[i] %= 10;
int now = lim;
while(!ans[now]) now--;
drep(i,now,0,1) cout<<ans[i];cout<<'\n';
}
NTT
其实和 FFT 没啥区别,但是建议学明白 FFT 后再看。
考虑 FFT 的弊端,复数为 double 类型,常数大,而且有精度误差。
那么什么时候可以用整数代替 double,当有模数的时候就行了。
为什么用单位根当 FFT 代入的那几个数,因为单位根有许多优秀的性质,而在模意义下,原根同样有类似的性质。
以下记模数为 \(Mod\),\(g\) 为 \(Mod\) 的原根(假设下文所说的东西在模 \(Mod\) 的意义下一定都存在)。
其实就是将 \(w_n\) 替换为 \(g^{\frac{Mod-1}{n}}\),然后那几个性质一样证明就好了。
但是我们要保证 \(n|(Mod-1)\),而又因为 \(n\) 一直为 \(2\) 的整数次幂,所以就要保证 \(Mod-1\) 为 \(p2^k\),其中 \(2^k\ge n\)
就比如常用模数 \(998244353=7\times17\times2^{23}+1\),所以它最多可以做 \(n=8388608=2^{23}\) 的 NTT。
代码实现和 FFT 没什么两样,还是以 【模板】多项式乘法(FFT) 为例。
确实比 FFT 快一点,但是我的 FFT 因为懒所以没有手写 complex 类,不知道手写以后会不会和 NTT 差不多。
code
#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t;i += p)
#define drep(i,s,t,p) for(int i = s;i >= t;i -= p)
#ifdef LOCAL
auto I = freopen("in.in","r",stdin),O = freopen("out.out","w",stdout);
#else
auto I = stdin,O = stdout;
#endif
using ll = long long;using ull = unsigned long long;
using db = double;using ldb = long double;
const int N = 4e6 + 10,Mod = 998244353,G = 3,Gi = 332748118;
int n,m,a[N],b[N],to[N],ct;
int qpow(int a,int b,int Mod = Mod){
int res = 1;
for(;b;b >>= 1,a = 1ll*a*a%Mod)
if(b&1) res = 1ll*res*a%Mod;
return res;
}
void ntt(int *a,int n,bool type){
rep(i,0,n-1,1) if(i < to[i]) swap(a[i],a[to[i]]);
for(int mid = 1;mid < n;mid <<= 1){
int W = qpow(type?G:Gi,(Mod-1)/(mid<<1));
for(int Res = mid<<1,j = 0;j < n;j += Res){
int w = 1;
for(int k = 0;k < mid; ++k,w = 1ll*w*W%Mod){
int x = a[j+k],y = 1ll*w*a[j+k+mid]%Mod;
a[j+k] = (x+y)%Mod;
a[j+k+mid] = (x-y+Mod)%Mod;
}
}
}
}
signed main(){
cin.tie(nullptr)->sync_with_stdio(false);
cin>>n>>m;rep(i,0,n,1) cin>>a[i];rep(i,0,m,1) cin>>b[i];
int lim = 1;while(lim <= (n+m)) lim <<= 1,ct++;
rep(i,0,lim,1) to[i] = (to[i>>1]>>1)|((i&1)<<(ct-1));
ntt(a,lim,true);ntt(b,lim,true);
rep(i,0,lim,1) a[i] = 1ll*a[i]*b[i]%Mod;
ntt(a,lim,false);
int Inv = qpow(lim,Mod-2,Mod);
rep(i,0,n+m,1) cout<<1ll*a[i]*Inv%Mod<<' ';cout<<'\n';
}
UPD
附赠一个比较快的多项式半家桶。link
本文来自博客园,作者:CuFeO4,转载请注明原文链接:https://www.cnblogs.com/hzoi-Cu/p/18697705




 浙公网安备 33010602011771号
浙公网安备 33010602011771号