[BZOJ2111]Perm排列计数
数论的坑深似海，组合数学就是个大海沟据教练所说这道题已经算简单的组合数学的题，然而我依旧是个废物
Perm 排列计数
内存限制：512 MiB 时间限制：1000 ms 标准输入输出
题目描述
输入格式
输出格式
样例
数据范围与提示
其实吧这道题仔细想想还真不太难，要求是$P_i>P_{\frac{i}{2}}$，他不仅包含偶数，还包含了奇数向下取整，那根据这个关系，我们其实可以构造出一个二叉树或者说是小根堆，如下图(WPS手工制作，有点丑)
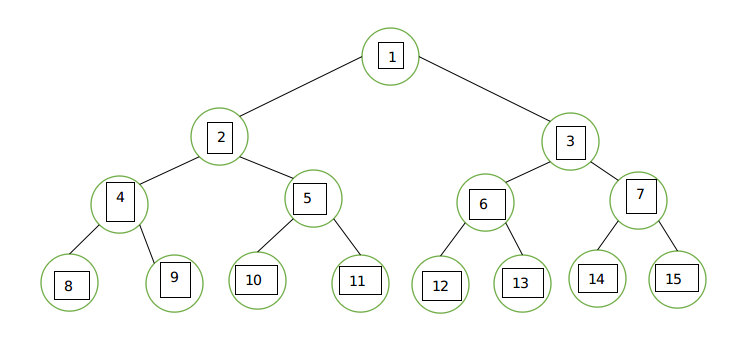
这样的话设以点i为根的符合条件的树有f[i]个，那么
$f[i]=f[i{\times}2]{\times}f[i{\times}2+1]$
可是我们会发现树中的部分子树交换位置不会影响小根堆的成立，那么不影响的有多少种呢？
设以i为根的子树大小为size[i]
则共有$C_{size[i]+1}^{size[2{\times}i]}$种
到此我们就可以知道
$f[i]=f[i{\times}2]{\times}f[i{\times}2+1]{\times}C_{size[i]+1}^{size[2{\times}2]}$
关于c的求解，由于n达到了$10^6$，所以需要用到Lucas定理，不会的可自行百度，不太难，Lucas+预处理逆元和阶乘就可以搞定c的求解
我求逆元的方法选择的是快速幂倒推，就会出现n>p时要特殊处理的情况，不然直接逆推所有的逆元都会变成0
还有就是注意一下long long我反正是死了
1 #include<iostream> 2 #include<cstdio> 3 #define maxn 10001000 4 #define ll long long 5 using namespace std; 6 ll ny[maxn],jc[maxn],size[maxn],f[maxn]; 7 ll n,p; 8 ll ksm(ll a,ll b,ll c) 9 { 10 ll ans=1; 11 a=a%c; 12 while(b>0) 13 { 14 if(b&1) ans=(ans*a)%c; 15 b=b>>1; 16 a=(a*a)%c; 17 } 18 return ans%c; 19 } 20 ll c(ll x,ll y)//Lucas定理求c 21 { 22 if(x<y) return 0; 23 if(x<p&&y<p) return ((jc[x]*ny[x-y])%p*ny[y])%p; 24 return (c(x/p,y/p)*c(x%p,y%p))%p; 25 } 26 int main() 27 { 28 //freopen("shuju.in","r",stdin); 29 //freopen("WA.out","w",stdout); 30 scanf("%lld%lld",&n,&p); 31 jc[0]=1; jc[1]=1; 32 for(int i=2;i<=n;++i) jc[i]=(jc[i-1]*i)%p;//求阶乘 33 if(p<=n)//关于n>=p的特殊处理 34 { 35 //cout<<ksm(jc[p-1],p-2,p)<<endl; 36 ny[p-1]=ksm(jc[p-1],p-2,p); 37 for(int i=p-1;i>=1;--i) ny[i-1]=(ny[i]*i)%p; 38 } 39 else 40 { 41 ny[n]=ksm(jc[n],p-2,p); 42 for(int i=n;i>=1;--i) ny[i-1]=(ny[i]*i)%p; 43 } 44 /*for(int i=1;i<=n;++i) 45 cout<<i<<" "<<jc[i]<<" "<<ny[i]<<endl;*/ 46 for(int i=n+1;i<=2*n+1;++i) f[i]=1;//预处理出等于一的部分f 47 for(int i=n;i>=1;--i) 48 { 49 size[i]=size[i*2]+size[i*2+1]+1; 50 f[i]=((f[i*2]*f[i*2+1])%p*c(size[i]-1,size[i*2]))%p; 51 //cout<<"c="<<c(size[i]-1,size[i*2])<<endl; 52 } 53 printf("%lld\n",f[1]); 54 /*cout<<"f="<<endl; 55 for(int i=1;i<=n;++i) cout<<f[i]<<" "; 56 cout<<endl;*/ 57 return 0; 58 }
随手附赠我调代码时搞出来的随机数据生成，质数虽然不全，但是调出来基本够用了
1 #include<bits/stdc++.h> 2 using namespace std; 3 int zs[45]={2,3,5,7,11,13,17,19,23,29,31,37,12281,16381,21841,29123,38833,51787,69061,92083,122777,163729,218357,291143,388211,517619,690163, 4 999983,1226959,1635947,2181271,2908361,3877817,5170427,6893911,9191891,2255871,16341163,21788233,29050993,38734667,51646229,68861641,91815541}; 5 int random(int x) 6 { 7 return rand()*rand()%x; 8 } 9 int main() 10 { 11 freopen("shuju.in","w",stdout); 12 srand(time(0)); 13 int n=random(100)+1,p=random(45); 14 if(n<0) n=-n; 15 if(p<0) p=-p; 16 cout<<n<<" "<<zs[p]<<endl; 17 return 0; 18 }
