浅谈计数排序

计数排序是一种非基于比较的排序算法，本文主要介绍计数排序的思想及代码实现

Ⅱ、分析问题

对于数组\(a_1\sim a_n\)，将其从小至大排序
步骤：
1、处理出数据中每个数出现的频率，放入数组\(b\)中
2、处理处数据频率表的前缀形式，此时第\(i\)个位置的数据表示\(a\)数组的全部数据中，小于等于\(a_i\)的数量（包括a_i本身）
3、依照前缀表处理出排好序的数组
例如，现在有数组\(a=\begin{Bmatrix}7,3,2,2,6,3,7,9,8,9\end{Bmatrix}\)，用计数排序将其排序

处理出\(a\)数组的频次表

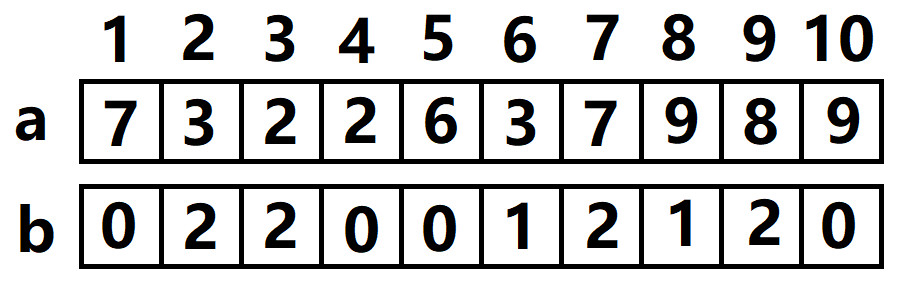
处理出b数组的前缀和

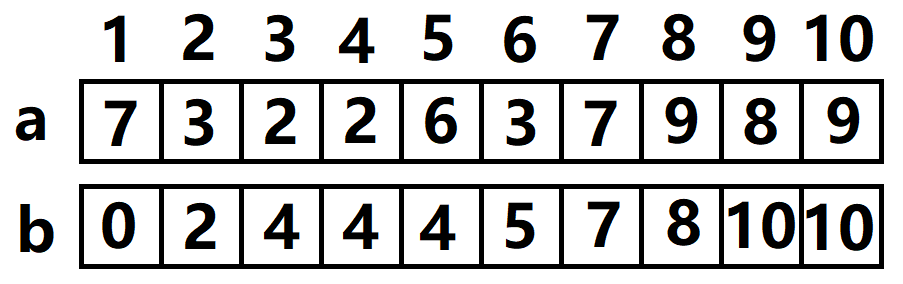
此时处理出前缀和之后，可以发现，\(i\)对应的\(a_i\)，恰好为\(i\)对应在排好序中的序列的最后一位的编号（或者没有）
于是代码就可以这么写：

#include<bits/stdc++.h>
#define F(i,j,n) for(register int i=j;i<=n;i++)
#define INF 0x3f3f3f3f
#define ll long long
#define mem(i,j) memset(i,j,sizeof(i))
using namespace std;
int n,m,a[100010],b[100010],c[100010];
inline int read(){
    int datta=0;char chchc=getchar();bool okoko=0;
    while(chchc<'0'||chchc>'9'){if(chchc=='-')okoko=1;chchc=getchar();}
    while(chchc>='0'&&chchc<='9'){datta=datta*10+chchc-'0';chchc=getchar();}
    return okoko?-datta:datta;
}
int main(){
	n=read();m=read();
	F(i,1,n)
		a[i]=read(),b[a[i]]++;//b数组用来处理频率
	F(i,1,m)
		b[i]+=b[i-1];//处理前缀和
	F(i,1,n)
		c[b[a[i]]--]=a[i];//将a[i]放入对应c数组的位置中，并将频率减一，可以手动模拟下
	F(i,1,n)
		printf("%d ",c[i]);
    return 0;
}