浅谈BST中的Splay
Ⅰ、预备知识
\(Splay\),二叉查找树(BST,Binary Search Tree)的一种。
其性质满足中序遍历是严格上升的,即左子树中所有数的键值<根节点的键值<右子树中所有数的键值,这一特点,一般支持一下几种操作:
1、插入一个权值为v的数
2、删除一个权值为v的数
3、查询v数的排名
4、查询排名为x的数
5、求v的前驱
6、求v的后继
类似能实现这些操作的BST还有比如非旋treap、fhq_treap、SBT等,均有各自数据结构的特点(蒟蒻全都不会)
不过,写旋转treap的都是sb
Ⅱ、分析问题
先让我们丢一道题出来
题目描述
您需要写一种数据结构,来维护一些数,其中需要提供以下操作:
1、插入\(x\)数
2、删除\(x\)数(若有多个相同的数,应只删除一个)
3、查询\(x\)数的排名(排名定义为比当前数小的数的个数\(+1\)。若有多个相同的数,应输出最小的排名)
4、查询排名为\(x\)的数
5、求\(x\)的前驱(前驱定义为小于\(x\),且最大的数)
6、求\(x\)的后继(后继定义为大于\(x\),且最小的数)
输入输出格式
输入格式:
第一行为\(n\),表示操作的个数,下面\(n\)行每行有两个数\(opt\)和\(x\),\(opt\)表示操作的序号\((1\leq opt\leq6)\)
输出格式:
对于操作\(3,4,5,6\)每行输出一个数,表示对应答案
输入输出样例
输入样例#1:
10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598
输出样例#1:
106465
84185
492737
说明:
时空限制:\(1000ms\),\(128M\)
的数据范围:\(n\leq100000\)
每个数的数据范围:\([-10^7,10^7]\)
先来随手扯一颗\(Splay\)树
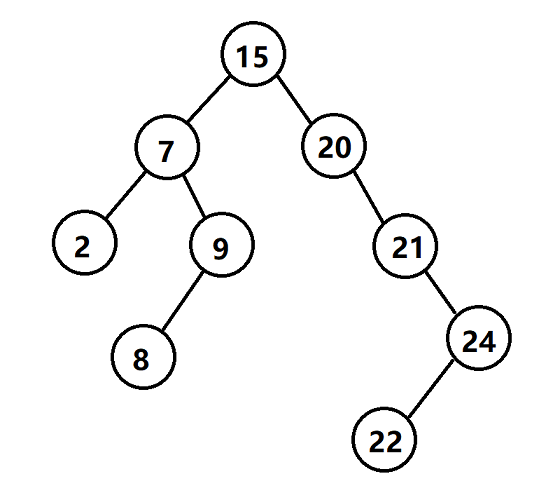
它是长这样的↑,符合前面说的\(Splay\)的性质
但是,在某些情况下,它可能会被卡成这样
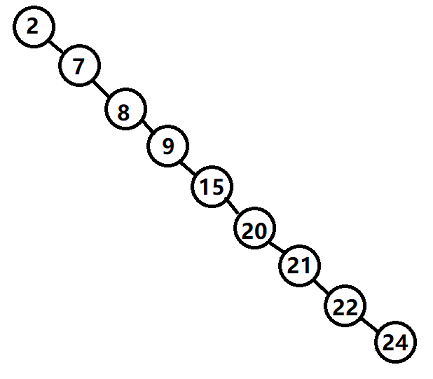
很明显可以看出,树的深度越大,时间复杂度越高
为了应对友(wu)好(liang)出题人把你的树卡成链,\(Splay\)最具代表性的操作\(rotate\)(划重点)出现了,它可以将一个节点旋转到其父节点位置而不破坏平衡树性质
如图
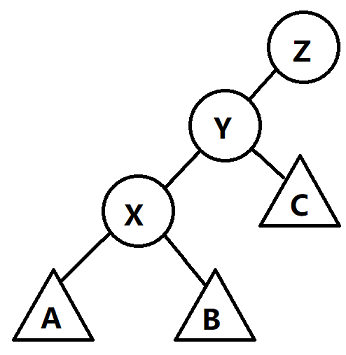
这是一颗\(Splay\)树,我们暂且觉得它很丑\(rotate\)操作将\(X\)结点旋转至\(Y\)结点后,它是这样的
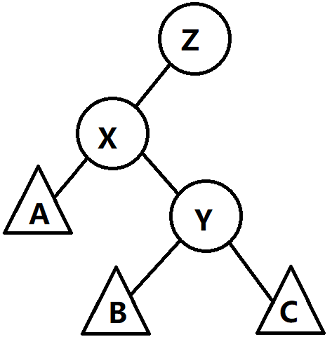
旋转后\(X\)的深度上升了,并且我们会发现\(Splay\)的性质仍未改变,这就非常的\(Nice\)和玄妙。通过\(rotate\)操作,我们可以维护一颗\(Splay\)树的性质,将任何一个节点旋转到根;同时,我们将由左图到右图\(Y\)变为\(X\)的右儿子的操作称为右旋(zig)操作;由右图到左图\(X\)变为\(Y\)的左儿子的操作称为左旋(zag)操作

\(rotate\)操作代码(以下注释以右旋操作为例说明):
inline void rot(int u){
bool kd=son[fa[u]][0]==u;//1右旋,0左旋
int gf=fa[fa[u]],f=fa[u],sn=son[u][kd];
son[f][!kd]=sn;
if(sn)
fa[sn]=f;
son[u][kd]=f;
fa[f]=u;
if(gf)
son[gf][f==son[gf][1]]=u;
fa[u]=gf;
updata(u);
updata(f);
}
inline void splay(int u,int target){
while(fa[u]!=target)
rot(u);
if(!target)
rt=u;
}
class Splay{
private:
int tot,rt,cnt[100010],val[100010],son[100010][2],fa[100010],sz[100010];
public:
inline void destroy(int u){
val[u]=cnt[u]=son[u][0]=son[u][1]=sz[u]=fa[u]=0;
}
inline void updata(int u){
sz[u]=sz[son[u][0]]+sz[son[u][1]]+cnt[u];
}
inline void rot(int u){
bool kd=son[fa[u]][0]==u;//1右旋,0左旋
int gf=fa[fa[u]],f=fa[u],sn=son[u][kd];
son[f][!kd]=sn;
if(sn)
fa[sn]=f;
son[u][kd]=f;
fa[f]=u;
if(gf)
son[gf][f==son[gf][1]]=u;
fa[u]=gf;
updata(u);
updata(f);
}
inline void splay(int u,int target){
while(fa[u]!=target)
rot(u);
if(!target)
rt=u;
}
inline int search(int u,int v){
while(val[u]!=v){
if(val[u]>v)
if(!son[u][0])
break;
else
u=son[u][0];
else
if(!son[u][1])
break;
else
u=son[u][1];
}
return u;
}
inline void ins(int v){
if(!tot){
val[++tot]=v;
rt=cnt[1]=sz[1]=1;
return ;
}
int u=search(rt,v);
if(val[u]==v){
cnt[u]++;
sz[u]++;
splay(u,0);
return ;
}
val[++tot]=v;
cnt[tot]=sz[tot]=1;
fa[tot]=u;
son[u][v>val[u]]=tot;
splay(tot,0);
}
inline int get_most(int u,bool kd){
if(!kd)
return search(u,-2147483647);
else
return search(u,2147483647);
}
inline int get_pre(int v){
int u=search(rt,v);
splay(u,0);
if(val[u]<v)
return u;
return get_most(son[u][0],1);
}
inline int get_nxt(int v){
int u=search(rt,v);
splay(u,0);
if(val[u]>v)
return u;
return get_most(son[u][1],0);
}
inline int kth_most(int u,int k,bool kd){
while(u){
if(k>sz[son[u][kd]]+cnt[u]){
k=k-(sz[son[u][kd]]+cnt[u]);
u=son[u][!kd];
}else{
if(k<=sz[son[u][kd]]){
u=son[u][kd];
}else{
splay(u,0);
break;
}
}
}
return u;
}
inline int get_rank(int v){
int u=search(rt,v);
splay(u,0);
if(val[u]>=v)
return sz[son[u][0]]+1;
else
return sz[son[u][0]]+cnt[u]+1;
}
inline void del(int v){
int u=search(rt,v);
if(val[u]!=v)
return;
if(--cnt[u]){
splay(u,0);
return;
}else{
splay(u,0);
if(!son[u][0]){
fa[son[u][1]]=0;
rt=son[u][1];
destroy(u);
return ;
}
if(!son[u][1]){
fa[son[u][0]]=0;
rt=son[u][0];
destroy(u);
return ;
}
fa[son[u][0]]=0;
splay(get_most(son[u][0],1),0);
son[rt][1]=son[u][1];sz[rt]+=sz[son[u][1]];
if(son[rt][1])
fa[son[rt][1]]=rt;
destroy(u);
}
}
inline int kth(int k,bool kd){
return val[kth_most(rt,k,kd)];
}
inline int pre(int v){
return val[get_pre(v)];
}
inline int nxt(int v){
return val[get_nxt(v)];
}
}S;


 浙公网安备 33010602011771号
浙公网安备 33010602011771号