实验三

实验任务一

运行截图：

回答问题：
1.函数score_to_grade的功能是作为一个新函数，对输入的分数进行ABCDE的打分
形参类型：int类型
返回值类型：char类型
2.类型不匹配：ans是char类型，修改后是const char类型，与char类型不匹配
缺少break语句：导致如果score/10是10或9时，也会继续执行后续case分支的赋值操作

实验任务二

运行截图：

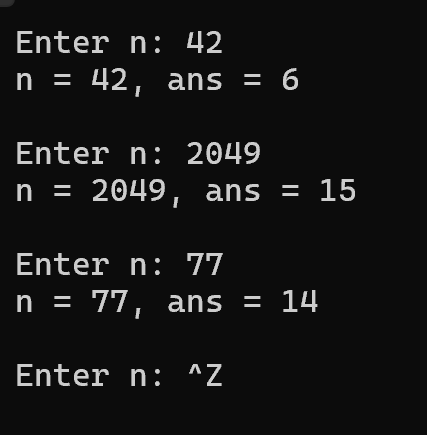
回答问题：
1.功能是计算一个整数的各位数字之和
2。能实现同样效果，迭代方式通过循环控制逐步计算，而递归方式通过函数自身调用和分解问题来实现相同的计算目标

实验任务三

运行解图：

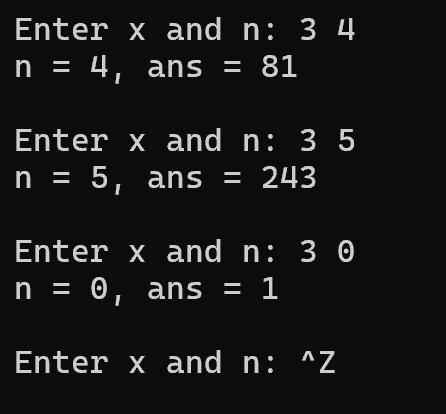
回答问题：
1.函数 power 的功能是计算 x 的 n 次幂并返回结果
2.是递归函数，

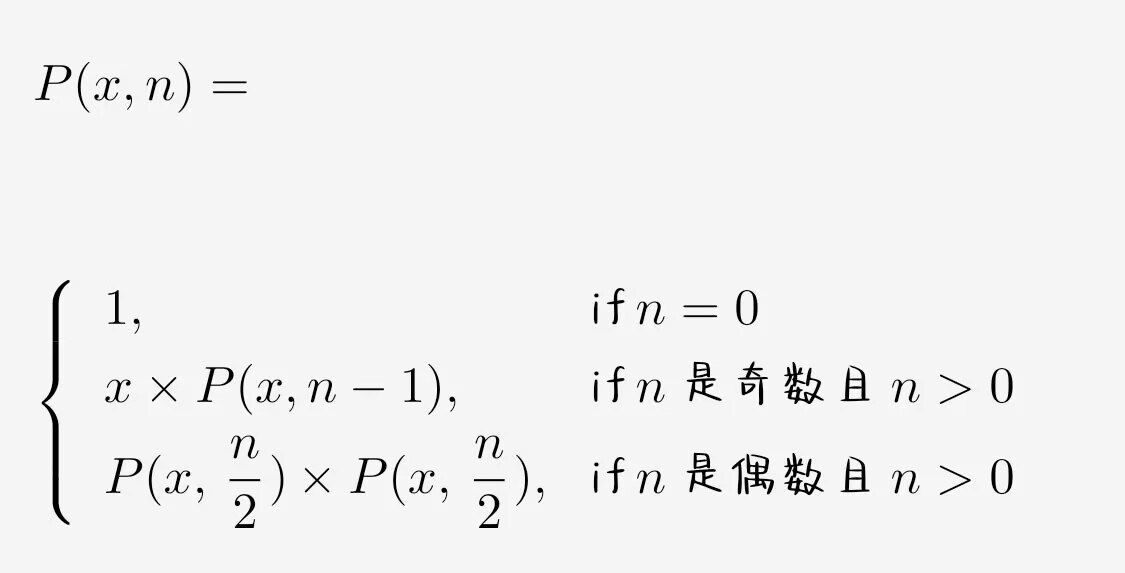
实验任务四

源代码：

点击查看代码

#include <stdio.h>
#include <math.h>

int is_prime(int n);  // 函数声明

int main() {
    int count;
    count = 0;

    printf("100以内的孪生素数:\n");
    for (int i = 3; i + 2 <= 100; i++) {
        if (is_prime(i) && is_prime(i + 2)) {
            printf("%d %d\n", i, i + 2);
            count++;
        }
    }
    printf("100以内的孪生素数共有%d个",count);

    return 0;
}

// 函数定义
    int is_prime(int n) {
    if (n <= 1)return 0;
    for (int i = 2; i <= sqrt(n); i++)
    {
        if (n % i == 0) {
            return 0;
        }
    }
    return 1;
}

实验任务五

源代码：

点击查看代码

#include <stdio.h>

int hanoi(unsigned int n, char from, char temp, char to);
void moveplate(unsigned int n, char from, char to);

int main()
{
    unsigned int n;
    while (scanf_s("%u", &n) != EOF)
    {
        int count = hanoi(n, 'A', 'B', 'C');
        printf("一共移动了%d次\n", count);
    }
    return 0;
}

int hanoi(unsigned int n, char from, char temp, char to)
{
    int count = 0;

    if (n == 1)
    {
        moveplate(n, from, to);
        count++;
    }
    else
    {
        count += hanoi(n - 1, from, to, temp);
        moveplate(n, from, to);
        count++;
        count += hanoi(n - 1, temp, from, to);
    }
    return count;
}

void moveplate(unsigned int n, char from, char to)
{
    printf("%u: %c --> %c\n", n, from, to);
}

运行解图：

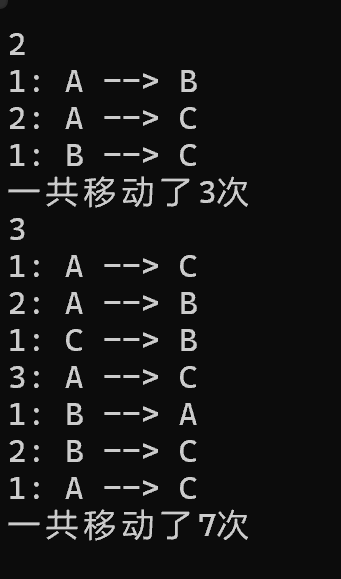
实验任务六

源代码：
递归：

点击查看代码

#include <stdio.h>


int func(int n, int m);

int main() {
    int n, m;
    int ans;

    while (scanf("%d%d", &n, &m) != EOF) {
        ans = func(n, m);
        printf("n = %d, m = %d, ans = %d\n", n, m, ans);
    }

    return 0;
}


int func(int n, int m) {

    if (m == 0 || m == n) {
        return 1;
    }

    return func(n - 1, m) + func(n - 1, m - 1);
}

迭代：

点击查看代码

#include <stdio.h>


int func(int n, int m);

int main() {
    int n, m;
    int ans;

    while (scanf_s("%d%d", &n, &m) != EOF) {
        ans = func(n, m);
        printf("n = %d, m = %d, ans = %d\n", n, m, ans);
    }

    return 0;
}


int func(int n, int m) {
    if (m > n) return 0;
    if (m == 0 || m == n) return 1;

    int result = 1;
    for (int i = 1; i <= m; i++) {
        result *= (n - i + 1) / i;
    }

    return result;
}

运行解图：

实验任务七：
源代码：

点击查看代码

#include <stdio.h>


int gcd(int a, int b);

int main() {
    int a, b, c;
    int ans;

    while (scanf_s("%d%d%d", &a, &b, &c) != EOF) {
        ans = gcd(gcd(a, b), c); // 先计算 a 和 b 的最大公约数，再计算结果与 c 的最大公约数
        printf("最大公约数：%d\n", ans);
    }

    return 0;
}

// 计算两个数的最大公约数
int gcd(int x, int y) {
    while (y != 0) {
        int temp = y;
        y = x % y;
        x = temp;
    }
    return x;
}

运行截图：