距离为K的节点 All Nodes Distance K in Binary Tree

2018-07-26 17:38:37

问题描述：

给定一个二叉树（具有根结点 root）， 一个目标结点 target ，和一个整数值 K 。

返回到目标结点 target 距离为 K 的所有结点的值的列表。 答案可以以任何顺序返回。

示例 1：

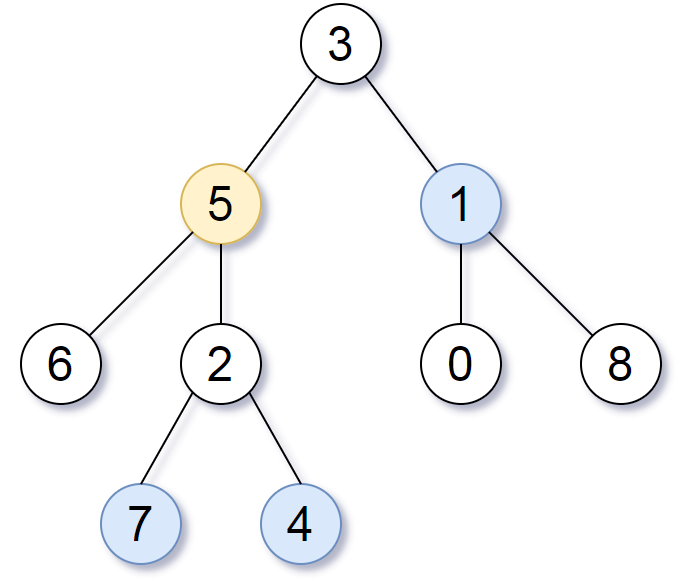
输入：root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2

输出：[7,4,1]

解释：
所求结点为与目标结点（值为 5）距离为 2 的结点，
值分别为 7，4，以及 1

注意，输入的 "root" 和 "target" 实际上是树上的结点。
上面的输入仅仅是对这些对象进行了序列化描述。

提示：

给定的树是非空的，且最多有 K 个结点。
树上的每个结点都具有唯一的值 0 <= node.val <= 500 。
目标结点 target 是树上的结点。
0 <= K <= 1000.

问题求解：

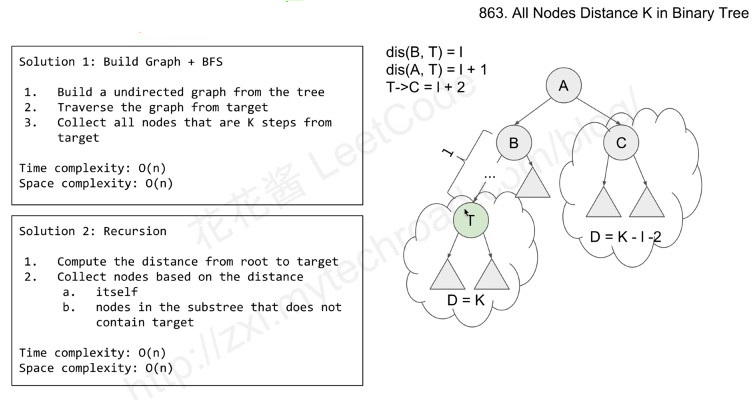
解法一、

第一种解法是使用Graph + BFS。换言之，就是将二叉树转化为无向图，然后在无向图中使用BFS进行层次遍历即可。

这种解法是比较直观的解法，是必须要进行掌握的，时间复杂度为O(n)。

    Map<TreeNode, Set<TreeNode>> graph = new HashMap<>();
    public List<Integer> distanceK(TreeNode root, TreeNode target, int K) {
        List<Integer> res = new ArrayList<>();
        dfs(root, null);
        Queue<TreeNode> q = new LinkedList<>();
        Set<TreeNode> used = new HashSet<>();
        q.add(target);
        used.add(target);
        int step = 0;
        while (!q.isEmpty() && step <= K) {
            int size = q.size();
            for (int i = 0; i < size; i++) {
                TreeNode curr = q.poll();
                if (step == K) res.add(curr.val);
                for (TreeNode next : graph.get(curr)) {
                    if (used.contains(next)) continue;
                    q.add(next);
                    used.add(next);
                }
            }
            step += 1;
        }
        return res;
    }
    
    private void dfs(TreeNode root, TreeNode parent) {
        if (root == null) return;
        if (!graph.containsKey(root)) graph.put(root, new HashSet<>());
        if (parent != null) {
            graph.get(root).add(parent);
            graph.get(parent).add(root);
        }
        dfs(root.left, root);
        dfs(root.right, root);
    }

 

解法二、

第二种解法自然就是递归解法了，本题的递归解法还是有点难度的，首先需要计算的是root 到 target的距离，如果距离值正好等于 K，那么就将当前的节点加入res，否则在另一个子树中进行collection。其次如果遍历到target，那么直接对target进行collection。

    public List<Integer> distanceK(TreeNode root, TreeNode target, int K) {
        List<Integer> res = new ArrayList<>();
        distance(root, target, K, res);
        return res;
    }

    private int distance(TreeNode root, TreeNode target, int K, List<Integer> res) {
        if (root == null) return -1;
        if (root == target) {
            collection(target, K, res);
            return 0;
        }

        int l = distance(root.left, target, K, res);
        int r = distance(root.right, target, K, res);

        if (l >= 0) {
            if (l == K - 1) res.add(root.val);
            collection(root.right,K - l - 2, res);
            return l + 1;
        }
        if (r >= 0) {
            if (r == K - 1) res.add(root.val);
            collection(root.left, K - r - 2, res);
            return r + 1;
        }
        return -1;
    }

    private void collection(TreeNode root, int K, List<Integer> res) {
        if (root == null || K < 0) return;
        if (K == 0) {
            res.add(root.val);
            return;
        }
        collection(root.left, K - 1, res);
        collection(root.right, K - 1, res);
    }