拓扑排序 Topological Sort
2018-05-02 16:26:07
一、拓扑排序
有向无环图(Directed acyclic graph,DAG)必定存在拓扑排序;非DAG没有拓扑排序一说。
二、拓扑排序算法
通常拓扑排序算法可以在O(n)的时间复杂度完成,具体来说是O(V + E)。
下面以leetcode207为例来介绍拓扑排序算法。
问题描述:

问题求解:
方法一、BFS
使用BFS求解拓扑排序是非常直观和简单的。
维护每个节点的indegree数目,对于入度为0的进队列,将所有入度为0的出队,并更新它们的邻接节点的indegree,若indegree == 0,入队。
循环以上操作直到队列为空。
public boolean canFinish(int numCourses, int[][] prerequisites) {
List<Integer>[] graph = new List[numCourses];
int[] indegree = new int[numCourses];
for (int i = 0; i < numCourses; i++) graph[i] = new ArrayList<>();
for (int[] edge : prerequisites) {
int from = edge[1];
int to = edge[0];
graph[from].add(to);
indegree[to] += 1;
}
int cnt = 0;
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < numCourses; i++) {
if (indegree[i] == 0) q.add(i);
}
while (!q.isEmpty()) {
int curr = q.poll();
cnt += 1;
for (int next : graph[curr]) {
indegree[next] -= 1;
if (indegree[next] == 0) q.add(next);
}
}
return cnt == numCourses;
}
方法二、DFS
使用DFS代码更为简洁。
实际就是给每个节点打上状态标签,如果访问到了正在访问的节点,那么必定存在环。
另外,我们需要一个访问完成的标签,避免重复访问已经访问过的节点。
public boolean canFinish(int n, int[][] edges) {
List<Integer>[] graph = new List[n];
for (int i = 0; i < n; i++) graph[i] = new ArrayList<>();
for (int[] e : edges) {
int from = e[1];
int to = e[0];
graph[from].add(to);
}
int[] state = new int[n];
for (int i = 0; i < n; i++) {
if (state[i] == 0 && !dfs(graph, i, state)) return false;
}
return true;
}
private boolean dfs(List<Integer>[] graph, int node, int[] state) {
state[node] = 1;
for (int next : graph[node]) {
if (state[next] == 2) continue;
if (state[next] == 1) return false;
if (!dfs(graph, next, state)) return false;
}
state[node] = 2;
return true;
}
三、拓扑排序应用
-
210. Course Schedule II
问题描述:

问题求解:
也是一条裸的拓扑排序题,相较于上一题,本题可以说是更纯粹的拓扑排序,因为不仅需要判环,还需要输出一个合法的解。当然,算法实现上也是两种思路,一是DFS,而是kahn算法。
DFS:
public int[] findOrder(int numCourses, int[][] prerequisites) {
int[] res = new int[numCourses];
List<Integer>[] graph = new List[numCourses];
for (int i = 0; i < numCourses; i++) graph[i] = new ArrayList<>();
for (int[] pair : prerequisites) {
graph[pair[1]].add(pair[0]);
}
int[] state = new int[numCourses];
Stack<Integer> s = new Stack<>();
for (int i = 0; i < numCourses; i++) {
if (state[i] == 0)
if (!dfs(graph, state, s, i)) return new int[0];
}
for (int i = 0; i < numCourses; i++) res[i] = s.pop();
return res;
}
private boolean dfs(List<Integer>[] g, int[] state, Stack<Integer> s, int i) {
if (state[i] == 2) return true;
if (state[i] == 1) return false;
state[i] = 1;
for (int node : g[i]) {
if (!dfs(g, state, s, node)) return false;
}
state[i] = 2;
s.push(i);
return true;
}
Kahn:
public int[] findOrder(int numCourses, int[][] prerequisites) {
int[] res = new int[numCourses];
int[] indegree = new int[numCourses];
List<Integer>[] graph = new List[numCourses];
for (int i = 0; i < numCourses; i++) graph[i] = new ArrayList<>();
for (int[] pair : prerequisites) {
graph[pair[1]].add(pair[0]);
indegree[pair[0]]++;
}
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < numCourses; i++) {
if (indegree[i] == 0)
q.add(i);
}
int cnt = 0;
while (!q.isEmpty()) {
int p = q.poll();
res[cnt++] = p;
for (int node : graph[p]) {
if (--indegree[node] == 0) q.add(node);
}
}
if (cnt == numCourses) return res;
else return new int[0];
}
- 1203. Sort Items by Groups Respecting Dependencies
问题描述:

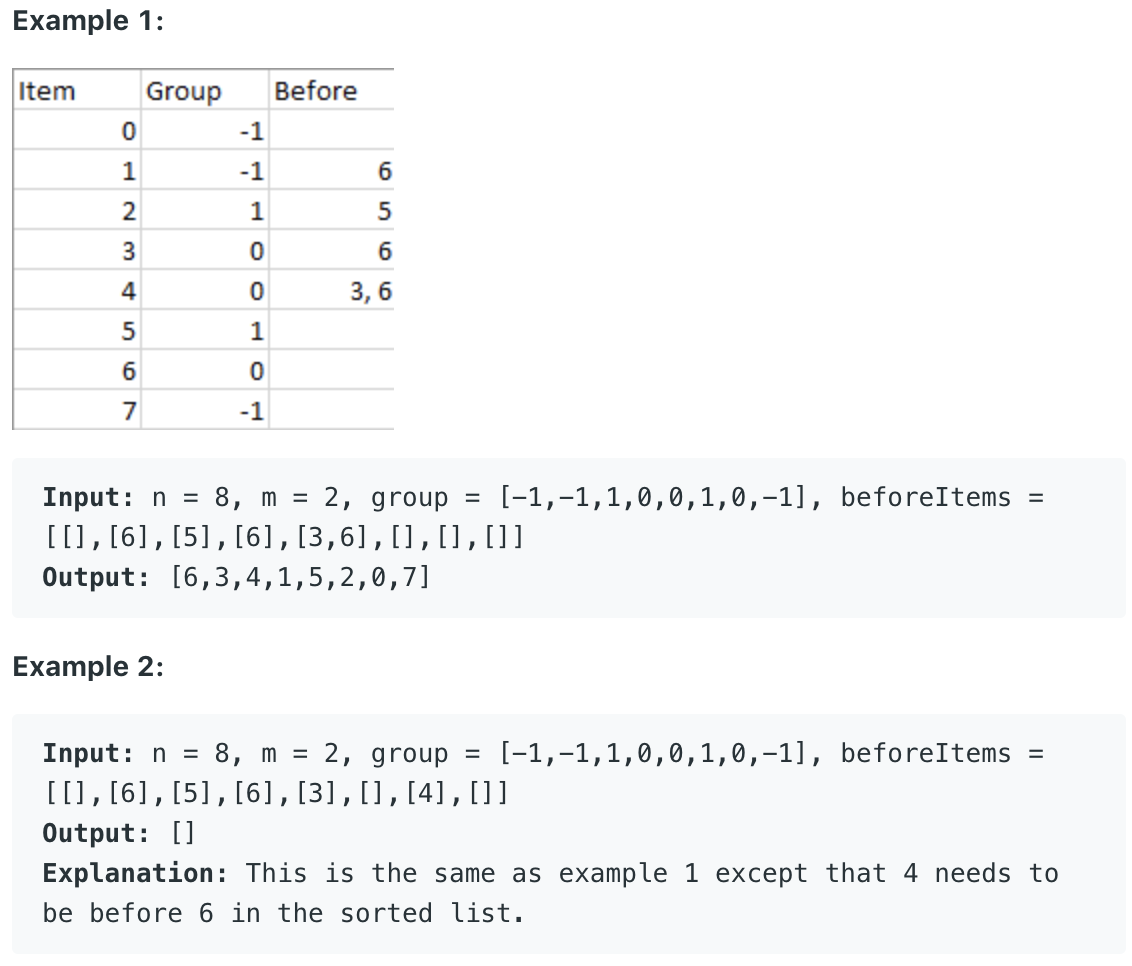

问题求解:
public int[] sortItems(int n, int m, int[] group, List<List<Integer>> beforeItems) {
Map<Integer, Set<Integer>> group2items = new HashMap<>();
Map<Integer, Set<Integer>> group_g = new HashMap<>();
Map<Integer, Integer> g_indegree = new HashMap<>();
Map<Integer, Set<Integer>> item_g = new HashMap<>();
Map<Integer, Integer> i_indegree = new HashMap<>();
int num_of_groups = m;
for (int i = 0; i < group.length; i++) {
if (group[i] == -1) group[i] = num_of_groups++;
}
for (int i = 0; i < num_of_groups; i++) {
group2items.put(i, new HashSet<>());
group_g.put(i, new HashSet<>());
g_indegree.put(i, 0);
}
for (int i = 0; i < n; i++) {
item_g.put(i, new HashSet<>());
i_indegree.put(i, 0);
group2items.get(group[i]).add(i);
}
for (int to = 0; to < beforeItems.size(); to++) {
int to_group = group[to];
for (int from : beforeItems.get(to)) {
int from_group = group[from];
if (to_group == from_group) {
item_g.get(from).add(to);
i_indegree.put(to, i_indegree.get(to) + 1);
}
else {
if (!group_g.get(from_group).contains(to_group)) {
group_g.get(from_group).add(to_group);
g_indegree.put(to_group, g_indegree.get(to_group) + 1);
}
}
}
}
// check groups
List<Integer> groups = new ArrayList<>();
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < num_of_groups; i++) {
if (g_indegree.get(i) == 0) {
q.add(i);
groups.add(i);
}
}
while (!q.isEmpty()) {
int cur = q.poll();
for (int to : group_g.get(cur)) {
g_indegree.put(to, g_indegree.get(to) - 1);
if (g_indegree.get(to) == 0) {
q.add(to);
groups.add(to);
}
}
}
if (groups.size() != num_of_groups) return new int[0];
// check items
List<Integer> res = new ArrayList<>();
for (int g : groups) {
int num = 0;
q = new LinkedList<>();
for (int item : group2items.get(g)) {
if (i_indegree.get(item) == 0) {
q.add(item);
res.add(item);
num += 1;
}
}
while (!q.isEmpty()) {
int cur = q.poll();
for (int to : item_g.get(cur)) {
i_indegree.put(to, i_indegree.get(to) - 1);
if (i_indegree.get(to) == 0) {
q.add(to);
res.add(to);
num += 1;
}
}
}
if (num != group2items.get(g).size()) return new int[0];
}
int[] ret = new int[res.size()];
for (int i = 0; i < res.size(); i++) ret[i] = res.get(i);
return ret;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号