数据结构-树状数组-区间修改单点求和-哈希-2251. 花期内花的数目

2022-04-30 20:06:01

问题描述：

给你一个下标从 0 开始的二维整数数组 flowers ，其中 flowers[i] = [starti, endi] 表示第 i 朵花的 花期 从 starti 到 endi （都 包含）。同时给你一个下标从 0 开始大小为 n 的整数数组 persons ，persons[i] 是第 i 个人来看花的时间。

请你返回一个大小为 n 的整数数组 answer ，其中 answer[i]是第 i 个人到达时在花期内花的 数目 。

 

示例 1：

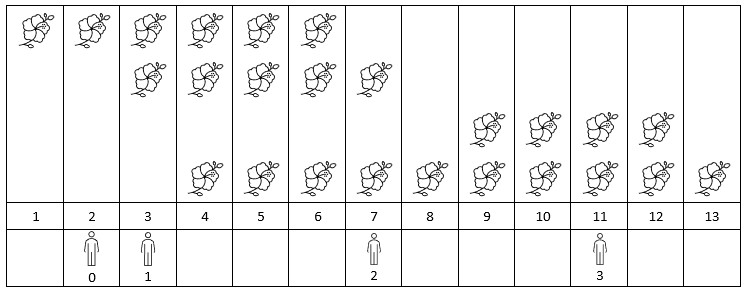
输入：flowers = [[1,6],[3,7],[9,12],[4,13]], persons = [2,3,7,11]
输出：[1,2,2,2]
解释：上图展示了每朵花的花期时间，和每个人的到达时间。
对每个人，我们返回他们到达时在花期内花的数目。

示例 2：

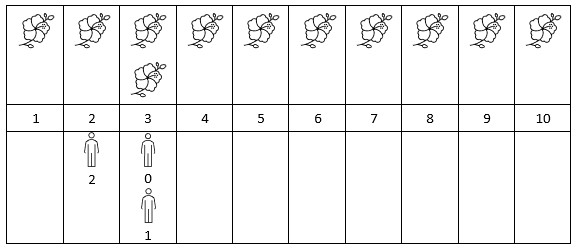
输入：flowers = [[1,10],[3,3]], persons = [3,3,2]
输出：[2,2,1]
解释：上图展示了每朵花的花期时间，和每个人的到达时间。
对每个人，我们返回他们到达时在花期内花的数目。

 

提示：

• 1 <= flowers.length <= 5 * 104
• flowers[i].length == 2
• 1 <= starti <= endi <= 109
• 1 <= persons.length <= 5 * 104
• 1 <= persons[i] <= 109

问题求解：

典型的区间修改，单点求和的问题，可以用树状数组高效求解。需要注意的是由于数据量过大，因此无法直接开数组，需要用哈希表对数据进行存储。

class Solution:
    def fullBloomFlowers(self, flowers: List[List[int]], persons: List[int]) -> List[int]:
        res = []
        n = int(1e9 + 7)

        def update(bit, idx, delta):
            i = idx
            while i < n:
                bit[i] += delta
                i += (i & -i)
        
        def query(bit, idx):
            res = 0
            i = idx
            while i > 0:
                res += bit[i]
                i -= (i & -i)
            return res
        
        bit = defaultdict(int)
        for l, r in flowers:
            update(bit, l, 1)
            update(bit, r + 1, -1)
        for p in persons:
            res.append(query(bit, p))
        return res