动态规划-区间dp-Palindrome Removal
2019-11-09 10:31:09
问题描述:
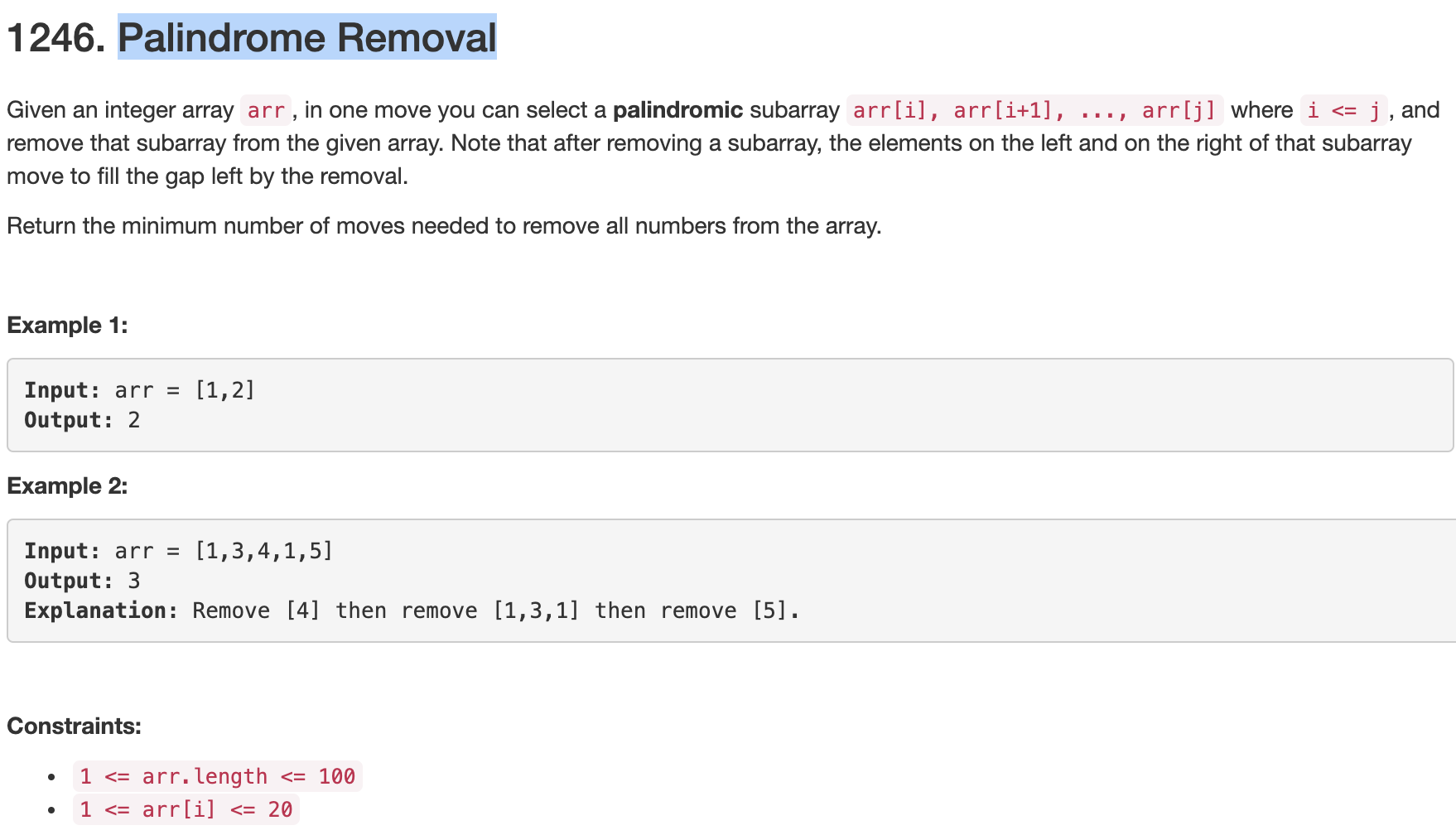
问题求解:
n = 100,典型的O(n ^ 3)的动规问题。一般来说这种O(n ^ 3)的问题可以考虑使用区间dp来解决。
区间dp是典型的三层结构,最外围枚举区间长度,中间层枚举起点,最里层枚举截断点,因此区间dp的时间复杂度往往为O(n ^ 3)。
public int minimumMoves(int[] arr) {
int n = arr.length;
int[][] dp = new int[n + 1][n + 1];
for (int i = 0; i < n; i++) dp[i][i] = 1;
for (int len = 2; len <= n; len++) {
for (int i = 0; i <= n - len; i++) {
int j = i + len - 1;
dp[i][j] = 1 + dp[i + 1][j];
if (arr[i] == arr[i + 1]) dp[i][j] = Math.min(dp[i][j], 1 + dp[i + 2][j]);
for (int k = i + 2; k <= j; k++) {
if (arr[k] == arr[i]) {
dp[i][j] = Math.min(dp[i][j], dp[i + 1][k - 1] + dp[k + 1][j]);
}
}
}
}
return dp[0][n - 1];
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号