【题解】P4250 [SCOI2015]小凸想跑步

题目链接

稍微讲点细节。

题意：给出一个凸多边形，点按 \(0\) ~ \(n-1\) 逆时针编号，现在有一个多边形内的随机点 \(P\) ，对于任意的 \(\triangle PP_iP_{i-1}\) 均满足

\[S_{\triangle PP_0P_1}< S_{\triangle PP_{i}P_{i-1} } \]

求满足条件的概率。按照几何概型实际上就是求满足条件的区域占总面积的比。

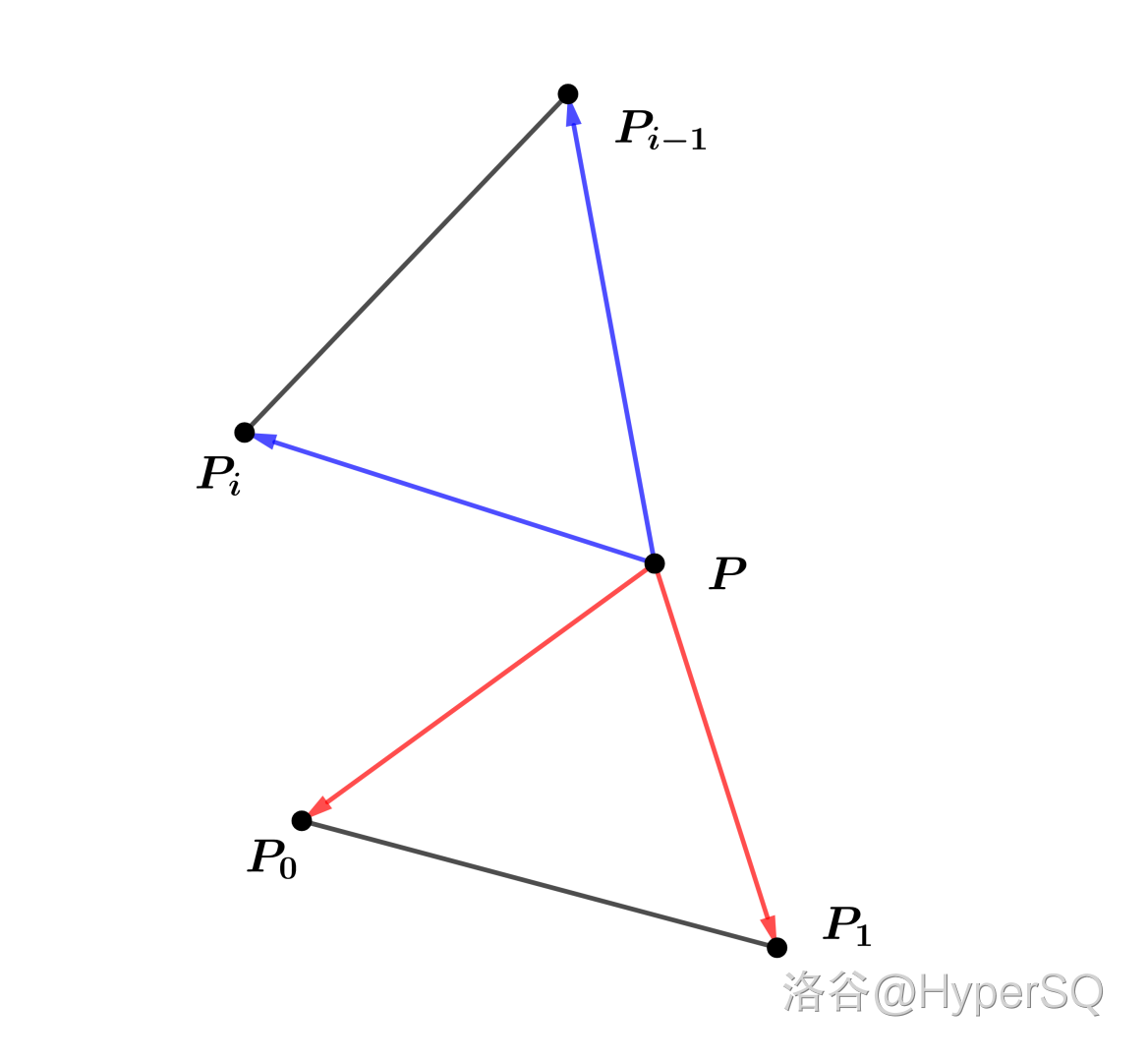
所以可知

\[\begin{aligned} \overrightarrow{PP_{0}}\times\overrightarrow{PP_{1}}&< \overrightarrow{PP_{i-1}}\times \overrightarrow{PP_{i}}\\ (x_{0}-x,y_0-y)\times(x_{1}-x,y_1-y)&< (x_{i-1}-x,y_{i-1}-y)\times(x_{i}-x,y_{i}-y)\\ \end{aligned} \]

容易整理得（就嗯算没啥技巧，所以过程不写了QwQ）

\[(y_0+y_i-y_1-y_{i-1})x+(x_1+x_{i-1}-x_0-x_i)y+x_0y_1+x_iy_{i-1}-x_1y_0-x_{i-1}y_i< 0 \]

是直线半平面的一般形式，这个式子我们简单记为 \(Ax+By+C<0 \Rightarrow By<-Ax-C\)。

所以对所有半平面求半平面交即可。

为了避免精度差，我们用点与向量来记录一条直线，向量左侧的空间就是这个直线对应的的半平面，所以向量方向不同会影响答案正确性。因此细节在于实现解析式转 \(l=\{P,\mathbf v\}\)。先对 \(B\) 的情况分类讨论。

1、\(B\) 不为 \(0\) 。

于是直线不与 \(y\) 轴平行，可知 \((0,-\frac{C}{B})\) 与 \((-B,-\frac{C}{B}+A)\) 为直线上两点。

讨论向量的方向。记向量角为 \(\theta\) 。原式 \(By<-Ax-C\) ，

当 \(B>0\) 对应下平面，应满足 \(\theta \in (\frac{\pi}{2},\frac{3\pi}{2})\) ； \(B<0\) 时为直线上平面，因此 \(\theta \in (-\frac{\pi}{2},\frac{\pi}{2})\)。

因此这个直线要满足：\(B\cos\theta<0\)。根据这个调整向量的方向。

2、\(B\) 为 \(0\)（一定要讨论这种情况，不然会错）

直线与 \(y\) 轴平行，此时经过点 \((-\frac{C}{A},0)\)。原式 \(Ax<-C\)。

当 \(A>0\) 时对应直线左平面，因此向量指向 \(\frac{\pi}{2}\) 角；

当 \(A<0\) 时对应直线右平面，因此向量指向 \(\frac{3\pi}{2}\) 。

因此要满足 \(A\sin\theta>0\)。

接下来就是板子了。

#include <bits/stdc++.h>
using namespace std;

const int maxn=4e5+5;
const double eps=1e-20;
#define Point complex<double>
#define Vector Point
#define Polygon vector<Point>
#define pb push_back
#define X real()
#define Y imag()

double cross(Vector u,Vector v){
    return u.X*v.Y-u.Y*v.X;
}
int sgn(double x){
    return x<-eps?-1:x>eps;
}

struct Line{
    Point p;Vector v;double a;
    Line(Point p=0,Vector v=0):v(v),p(p){
        a=arg(v);
    }
};

bool cmp(Line a,Line b){
    if(fabs(a.a-b.a)>eps) return a.a<b.a;
    return cross(b.p-a.p,a.v)>0;
}

Line l[maxn];int cnt;

bool on_left(Point p,Line l){
    return sgn(cross(l.v,p-l.p))>0;
}

void line_inter(Line a,Line b,Point &p){
    double c=cross(a.v,b.v);
    if(sgn(c)==0) return;
    p=a.p+a.v*cross(b.v,a.p-b.p)/c;
}

void halfplane_inter(Polygon &g){
    vector<Point> q(cnt);
    sort(l,l+cnt,cmp);
    int head=0,tail=0;
    for(int i=1;i<cnt;i++){
        if(!sgn(l[i].a-l[i-1].a)) continue;
        while(head<tail&&!on_left(q[tail-1],l[i])) tail--;
        while(head<tail&&!on_left(q[head],l[i])) head++;
        l[++tail]=l[i];
        if(head<tail) line_inter(l[tail-1],l[tail],q[tail-1]);
    }
    while(head<tail&&!on_left(q[tail-1],l[head])) tail--;
    if(head<tail) line_inter(l[tail],l[head],q[tail]);
    g.assign(q.begin()+head,q.begin()+tail+1);
}

double polygon_area(Polygon &g){
    double ret=0;
    for(int i=0;i<g.size()-1;i++){
        ret+=cross(g[i]-g[0],g[i+1]-g[0]);
    }
    ret/=2;return ret;
}

int n;
Polygon p,g;

int main(){
#ifdef LOCAL
    freopen("in.in","r",stdin);
    freopen("out.out","w",stdout);
#endif
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        double x,y;
        scanf("%lf%lf",&x,&y);
        p.pb(Point(x,y));
    }
    p.pb(p[0]);
    for(int i=2;i<=n;i++){
        double A=p[0].Y+p[i].Y-p[1].Y-p[i-1].Y;
        double B=-(p[0].X+p[i].X-p[1].X-p[i-1].X);
        double C=p[0].X*p[1].Y+p[i].X*p[i-1].Y-p[1].X*p[0].Y-p[i-1].X*p[i].Y;
        if(!sgn(B)){
            Point p1(-C/A,0);
            Vector v(0,A);
            if(sgn(A*sin(arg(v)))<0) v=-v;
            l[cnt++]=Line(p1,v);
        }else{
            Point p1(0,-C/B);
            Vector v(-B,A);
            if(sgn(cos(arg(v))*B)>0) v=-v;
            l[cnt++]=Line(p1,v);
        }
    }
    for(int i=0;i<n;i++){
        l[cnt++]=Line(p[i],p[i+1]-p[i]);
    }
    p.pop_back();
    halfplane_inter(g);
    double S=polygon_area(p);double s=polygon_area(g);
    if(s<0.0) puts("0.0000");
    else printf("%.4lf",s/S);
}