李航统计学习方法-第十章-习题代码学习-前向后向维特比

本文为李航《统计学习方法》第十章课后习题10.1-10.3答案

---

# -*-coding:utf-8-*-
import numpy as np
def sum(L):
    sumValue = 0.0
    for i in range(0, len(L)):
        sumValue += L[i]
    return sumValue
def max(L):
    target = 0
    maxValue = L[target]
    for i in range(1, len(L)):
        if (L[i] > maxValue):
            target = i
            maxValue = L[i]
    return maxValue, target + 1

def printTable(table, type="float"):
    if (type == "float"):
        for i in range(0, len(table)):
            for j in range(0, len(table[i])):
                print ("%-16f" % (table[i][j]),)
            print ("\n")
    elif (type == "int"):
        for i in range(0, len(table)):
            for j in range(0, len(table[i])):
                print ("%-2d" % (table[i][j]),)
            print ("\n")


def initTable(x, y, type="float"):
    table = []
    if (type == "float"):
        initValue = 0.0
    elif (type == "int"):
        initValue = 0
    for i in range(0, x):
        temp = []
        for j in range(0, y):
            temp.append(initValue)
        table.append(temp)
    return np.array(table)

def forwardV(A, B, pi, Object, mod="forward"):
    T = len(Object)
    NumState = len(A)
    NodeTable = initTable(NumState, T)
    if (mod == "viterbi"):
        NodePath = initTable(NumState, T, type="int")
    for i in range(0, NumState):
        NodeTable[i][0] = pi[i] * B[i][Object[0]]
    for t in range(1, T):
        for j in range(0, NumState):
            temp = []
            for i in range(0, NumState):
                temp.append(NodeTable[i][t - 1] * A[i][j] * B[j][Object[t]])
            if (mod == "forward"):
                NodeTable[j][t] = sum(temp)
            elif (mod == "viterbi"):
                NodeTable[j][t], NodePath[j][t] = max(temp)

    if (mod == "forward"):
        print (u"前向算法alpha值记录表：")
        printTable(NodeTable)
        p = 0.0
        for i in range(0, NumState):
            p += NodeTable[i][T - 1]
        return NodeTable, p

    elif (mod == "viterbi"):
        print (u"viterbi算法结点值记录表：")
        printTable(NodeTable)
        print (u"viterbi算法路径记录表：")
        printTable(NodePath, type="int")
        target = 0
        maxValue = NodeTable[target][T - 1]
        for i in range(1, NumState):
            if NodeTable[i][T - 1] > maxValue:
                target = i
                maxValue = NodeTable[i][T - 1]
        print (u"viterbi算法最终状态：", target + 1, "\n")
        StateSequeues = [0] * T
        StateSequeues[T - 1] = target + 1
        for i in range(1, T):
            StateSequeues[T - i - 1] = NodePath[StateSequeues[T - i] - 1][T - i]
        return StateSequeues

def backward(A, B, pi, Object):
    T = len(Object)
    NumState = len(A)
    NodeTable = initTable(NumState, T)
    for i in range(0, NumState):
        NodeTable[i][T - 1] = 1
    for t in range(1, T):
        for i in range(0, NumState):
            temp = []
            for j in range(0, NumState):
                temp.append(NodeTable[j][T - t] * A[i][j] * B[j][Object[T - t]])
            NodeTable[i][T - t - 1] = sum(temp)
    print (u"后向算法beta值记录表：")
    printTable(NodeTable)
    p = 0.0
    for i in range(0, NumState):
        p += pi[i] * B[i][Object[0]] * NodeTable[i][0]
    return NodeTable, p

# ---------------------------------------------------------------------#
# forwardV函数实现前向算法和viterbi算法
# backward函数实现后向算法的计算
# 前向后向结合计算特殊点概率，只需取两个记录表中相应的alpha和beta值即可
# ---------------------------------------------------------------------#
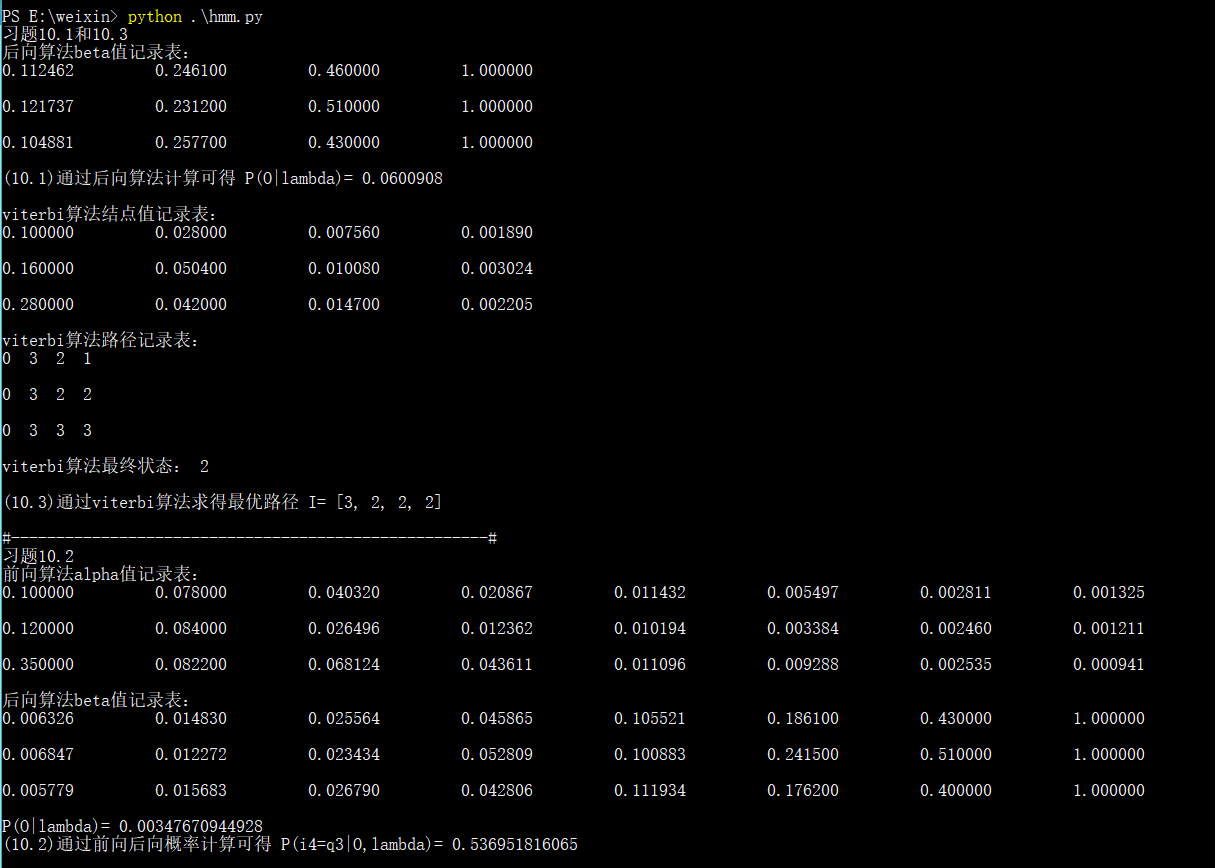
print (u"习题10.1和10.3")
A1 = [[0.5, 0.2, 0.3], [0.3, 0.5, 0.2], [0.2, 0.3, 0.5]]
B1 = [[0.5, 0.5], [0.4, 0.6], [0.7, 0.3]]
pi1 = [0.2, 0.4, 0.4]
Object1 = [0, 1, 0, 1]

# 习题10.1
table, P = backward(A1, B1, pi1, Object1)
print (u"(10.1)通过后向算法计算可得 P(O|lambda)=", P, "\n")

# 习题10.3
I = forwardV(A1, B1, pi1, Object1, mod="viterbi")
print (u"(10.3)通过viterbi算法求得最优路径 I=", I, "\n")

print (u"#-----------------------------------------------------#")
# ---------------------------------------------------------------------#
print (u"习题10.2")
A2 = [[0.5, 0.1, 0.4], [0.3, 0.5, 0.2], [0.2, 0.2, 0.6]]
B2 = [[0.5, 0.5], [0.4, 0.6], [0.7, 0.3]]
pi2 = [0.2, 0.3, 0.5]
Object2 = [0, 1, 0, 0, 1, 0, 1, 1]
F, pf = forwardV(A2, B2, pi2, Object2, mod="forward")
B, pb = backward(A2, B2, pi2, Object2)
# 习题10.2
# P(i4=q3|O,lambda)=P(i4=q3,O|lambda)/P(O|lambda)=alpha4(3)*beta4(3)/P(O|lamda)
# pf=pb,任选一个
# 1-based索引转换为0-based索引
print (u"P(O|lambda)=", pf)
P2 = F[3 - 1][4 - 1] * B[3 - 1][4 - 1] / pf
print (u"(10.2)通过前向后向概率计算可得 P(i4=q3|O,lambda)=", P2, "\n")