【优化】对偶上升法(Dual Ascent)超简说明
【优化】对偶上升法(Dual Ascent)超简说明
本文从便于理解的角度介绍对偶上升法,略去大部分数学推导,目的是帮助大家看懂论文中的相关部分。
阅读本文前,请先参看这篇博客《共轭函数超简说明》。
1</sup>
也称为拉格朗日对偶函数(Lagrange dual function)。
拉格朗日量
考虑定义域
D
D
D上的最小化问题:<br>
m
i
n
i
m
i
z
e
f
0
(
x
)
,
x
∈
D
minimize\ f_0(x), x\in D
minimize f0(x),x∈D
有
m
m
m个不等式约束,以及
p
p
p个等式约束:<br>
f
i
(
x
)
≤
0
,
i
=
1
,
2...
m
f_i(x)\leq0, i=1,2...m
fi(x)≤0,i=1,2...m
h
i
(
x
)
=
0
,
i
=
1
,
2...
p
h_i(x)=0, i=1,2...p
hi(x)=0,i=1,2...p
这个最优化问题的拉格朗日量(Lagrangian)为:
L
(
x
,
λ
,
ν
)
=
f
0
(
x
)
+
∑
i
=
1
m
λ
i
f
i
(
x
)
+
∑
i
=
1
p
ν
i
h
i
(
x
)
L(x,\lambda,\nu)=f_0(x)+\sum_{i=1}^m\lambda_if_i(x) + \sum_{i=1}^p\nu_ih_i(x)
L(x,λ,ν)=f0(x)+i=1∑mλifi(x)+i=1∑pνihi(x)
其物理意义参见这篇博客《拉格朗日乘子法超简说明》。
其中
λ
,
ν
\lambda, \nu
λ,ν称为拉格朗日乘子(Lagrange multiplier)或者对偶变量(dual variable),
x
x
x称为原变量(primal variable)。
拉格朗日量是关于
x
,
λ
,
ν
x,\lambda, \nu
x,λ,ν的函数。</p>
拉格朗日对偶函数
对于定义域
D
D
D上
x
x
x的所有取值,拉格朗日量的最小值即为拉格朗日对偶函数(dual function):<br>
g
(
λ
,
ν
)
=
inf
x
∈
D
L
(
x
,
λ
,
ν
)
g(\lambda, \nu)=\inf_{x\in D}L(x,\lambda, \nu)
g(λ,ν)=x∈DinfL(x,λ,ν)
拉格朗日对偶函数是关于对偶变量
λ
,
ν
\lambda, \nu
λ,ν的函数</p>
拉格朗日对偶函数可以看做是
x
x
x取不同值时一族曲线的下界(绿线)。<br> <img src="https://img-blog.csdnimg.cn/img_convert/86704d14fdf9b349d386151a669f4d1a.png" alt="这里写图片描述">
当
λ
≥
0
\lambda\geq0
λ≥0时,对于最优化问题的解
x
ˉ
\bar x
xˉ,两个约束条件都非正:<br>
λ
i
f
i
(
x
ˉ
)
<
=
0
,
ν
i
h
i
(
x
ˉ
)
=
0
\lambda_i f_i(\bar x)<=0, \ \nu_i h_i(\bar x)=0
λifi(xˉ)<=0, νihi(xˉ)=0
L
(
x
ˉ
,
λ
,
ν
)
≤
f
0
(
x
ˉ
)
L(\bar x,\lambda,\nu)\leq f_0(\bar x)
L(xˉ,λ,ν)≤f0(xˉ)
g
(
λ
,
ν
)
≤
f
0
(
x
ˉ
)
g(\lambda, \nu)\leq f_0(\bar x)
g(λ,ν)≤f0(xˉ)
换言之
λ
>
0
\lambda>0
λ>0时,拉格朗日对偶函数是最优化值的下界</strong>。</p>
对偶函数与共轭函数
考虑线性约束下的最优化问题
m
i
n
i
m
i
z
e
f
0
(
x
)
,
x
∈
D
minimize\ f_0(x), x\in D
minimize f0(x),x∈D
A
x
≤
b
,
C
x
=
d
Ax\leq b,Cx=d
Ax≤b,Cx=d
其对偶函数:
g
(
λ
,
ν
)
=
inf
x
(
f
0
(
x
)
+
λ
T
(
A
x
−
b
)
+
ν
T
(
C
x
−
d
)
)
g(\lambda, \nu)=\inf_x \left( f_0(x)+\lambda^T(Ax-b) + \nu^T(Cx-d)\right)
g(λ,ν)=xinf(f0(x)+λT(Ax−b)+νT(Cx−d))
提取和
x
x
x无关的项,凑出共轭函数形式:<br>
g
(
λ
,
ν
)
=
−
λ
T
b
−
ν
T
d
+
inf
x
(
f
0
(
x
)
+
λ
T
A
x
+
ν
T
C
x
)
g(\lambda, \nu)=-\lambda^Tb - \nu^Td + \inf_x \left( f_0(x)+\lambda^TAx + \nu^TCx\right)
g(λ,ν)=−λTb−νTd+xinf(f0(x)+λTAx+νTCx)
=
−
λ
T
b
−
ν
T
d
−
sup
x
(
(
−
A
T
λ
−
C
T
ν
)
T
x
−
f
0
(
x
)
)
=-\lambda^Tb - \nu^Td - \sup_x \left( (-A^T\lambda-C^T\nu)^Tx - f_0(x)\right)
=−λTb−νTd−xsup((−ATλ−CTν)Tx−f0(x))
=
−
λ
T
b
−
ν
T
d
−
f
∗
(
−
A
T
λ
−
C
T
ν
)
=-\lambda^Tb - \nu^Td - f^*(-A^T\lambda-C^T\nu)
=−λTb−νTd−f∗(−ATλ−CTν)
线性约束下的对偶函数可以用共轭函数表示。
其自变量为拉格朗日乘子的线性组合。
2</sup>
上图绿线上的最高点,是对于最优化值下界的最好估计:
m
a
x
i
m
i
z
e
g
(
λ
,
ν
)
maximize\ g(\lambda,\nu)
maximize g(λ,ν)
s
u
b
j
e
c
t
t
o
λ
≥
0
subject\ to\ \lambda \geq0
subject to λ≥0<br> 这个问题称为原优化问题的拉格朗日对偶问题(dual problem)。
如果
- 强对偶条件成立[3](#fn3)
- 对偶问题存在最优解
λ
ˉ
,
ν
ˉ
\bar \lambda,\bar \nu
λˉ,νˉ</li>
则:原问题
f
0
(
x
)
f_0(x)
f0(x)的最优解
x
ˉ
\bar x
xˉ也是
L
(
x
,
λ
ˉ
,
ν
ˉ
)
L(x,\bar \lambda,\bar \nu)
L(x,λˉ,νˉ)的最优解<sup class="footnote-ref">[3](#fn3)</sup>
L
(
x
,
λ
ˉ
,
ν
ˉ
)
L(x,\bar \lambda,\bar \nu)
L(x,λˉ,νˉ)是关于
x
x
x的函数,相当于在图中
[
λ
,
ν
]
=
[
λ
ˉ
,
ν
ˉ
]
[\lambda,\nu] = [\bar \lambda,\bar \nu]
[λ,ν]=[λˉ,νˉ]对应的竖线上,查找值最小曲线对应的
x
x
x。
换言之:
原问题和对偶问题通过拉格朗日量联系了起来。
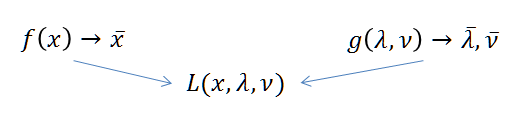
如果
f
(
x
)
f(x)
f(x)复杂,而
g
(
λ
,
ν
)
g(\lambda, \nu)
g(λ,ν)简单, 可以通过如下方式求解原问题:
x k + 1 = arg min x L ( x , λ k , ν k ) x^{k+1}=\arg \min_xL(x,\lambda^k,\nu^k) xk+1=argxminL(x,λk,νk)
λ k + 1 = λ k + α ⋅ ∂ L ( x , λ , ν ) ∂ λ ∣ x = x k + 1 , λ = λ k , ν = ν k \lambda^{k+1}=\lambda^k + \alpha \cdot \frac{\partial L(x,\lambda,\nu)}{\partial \lambda} |_{x=x^{k+1},\lambda=\lambda^{k}, \nu=\nu^{k}} λk+1=λk+α⋅∂λ∂L(x,λ,ν)∣x=xk+1,λ=λk,ν=νk
ν
k
+
1
=
λ
k
+
α
⋅
∂
L
(
x
,
λ
,
ν
)
∂
ν
∣
x
=
x
k
+
1
,
λ
=
λ
k
,
ν
=
ν
k
\nu^{k+1}=\lambda^k + \alpha \cdot \frac{\partial L(x,\lambda,\nu)}{\partial \nu} |_{x=x^{k+1},\lambda=\lambda^{k}, \nu=\nu^{k}}
νk+1=λk+α⋅∂ν∂L(x,λ,ν)∣x=xk+1,λ=λk,ν=νk
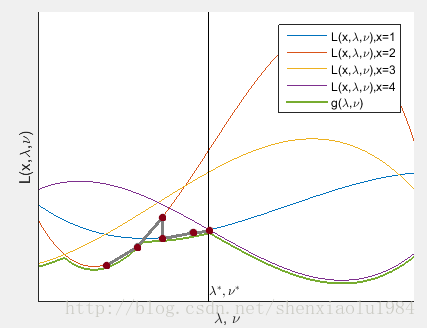
这一方法称为对偶上升法。下图的灰线示出解的变化:
- S. Boyd and L. Vandenberghe, Convex Optimization. Cambridge University Press, 2004. KaTeX parse error: Undefined control sequence: \S at position 1: \̲S̲ 5.1 ↩︎ 1. S. Boyd and L. Vandenberghe, Convex Optimization. Cambridge University Press, 2004. KaTeX parse error: Undefined control sequence: \S at position 1: \̲S̲ 5.2 ↩︎ 1. S. Boyd and L. Vandenberghe, Convex Optimization. Cambridge University Press, 2004. KaTeX parse error: Undefined control sequence: \S at position 1: \̲S̲ 5.5.5 ↩︎ ↩︎ 1. S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine Learning, 2011. KaTeX parse error: Undefined control sequence: \S at position 1: \̲S̲ 2.1 ↩︎
转载于网络 侵权联系作者立即删除QAQ


 浙公网安备 33010602011771号
浙公网安备 33010602011771号