数据分析第二次作业

import numpy as np
import pandas as pd

inputfile="D:\数据分析\data.csv"
data=pd.read_csv(inputfile)

description=[data.min(),data.max(),data.mean(),data.std()]
description=pd.DataFrame(description,index=['Min','Max','Mean','STD']).T
print('描述性统计结果:\n',np.round(description,2))

 

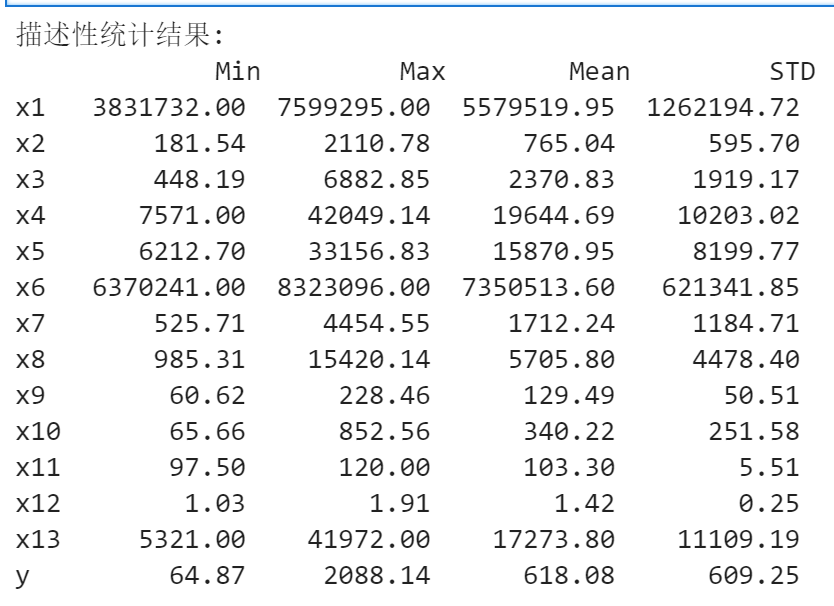
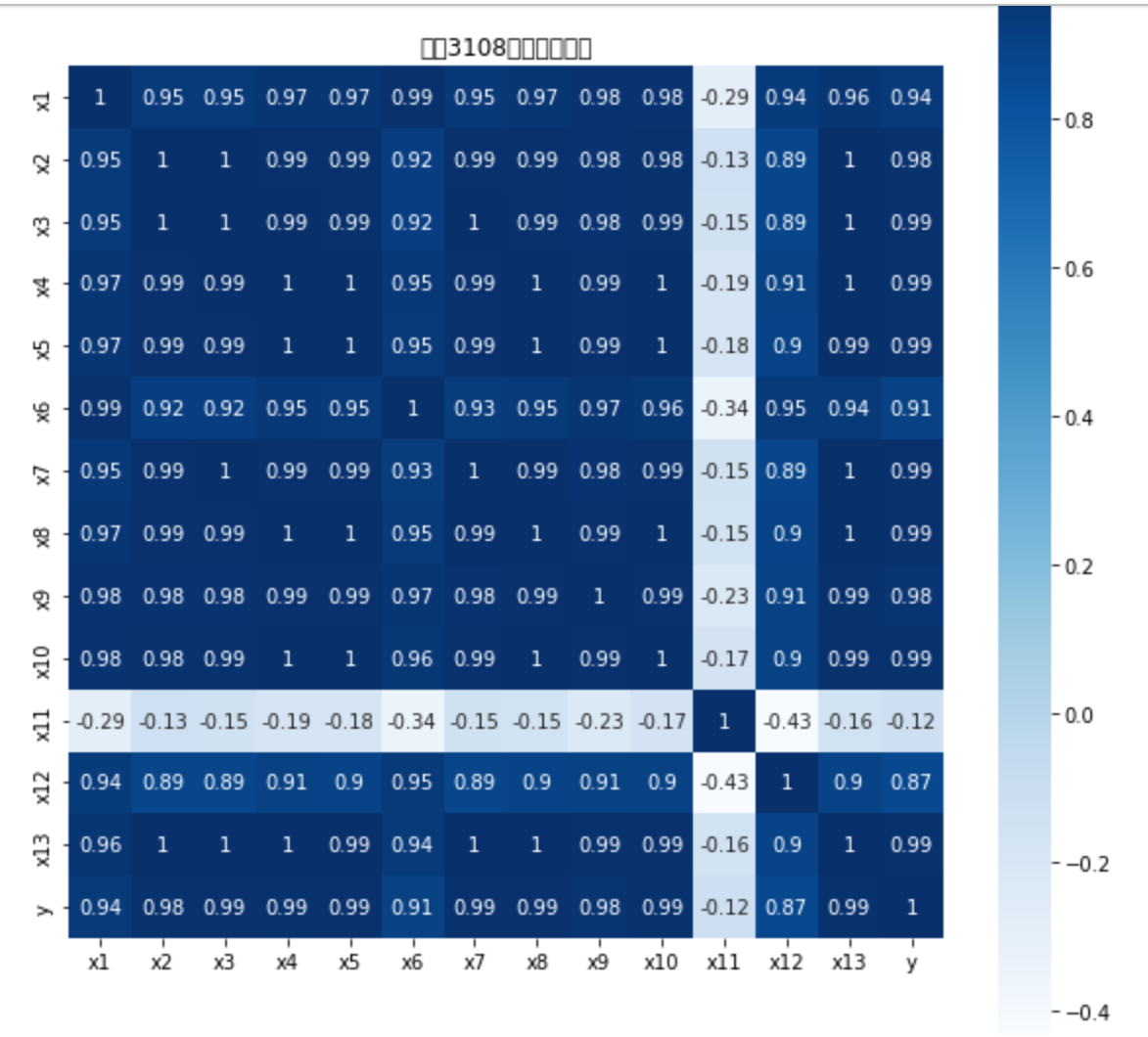
# 代码6-2

# 相关性分析
corr = data.corr(method = 'pearson')  # 计算相关系数矩阵
print('相关系数矩阵为：\n',np.round(corr, 2))  # 保留两位小数



# 代码6-3

# 绘制热力图
import matplotlib.pyplot as plt
import seaborn as sns
plt.subplots(figsize=(10, 10)) # 设置画面大小 
sns.heatmap(corr, annot=True, vmax=1, square=True, cmap="Blues") 
plt.title('学号3108相关性热力图')
plt.show()
plt.close

 

 

 

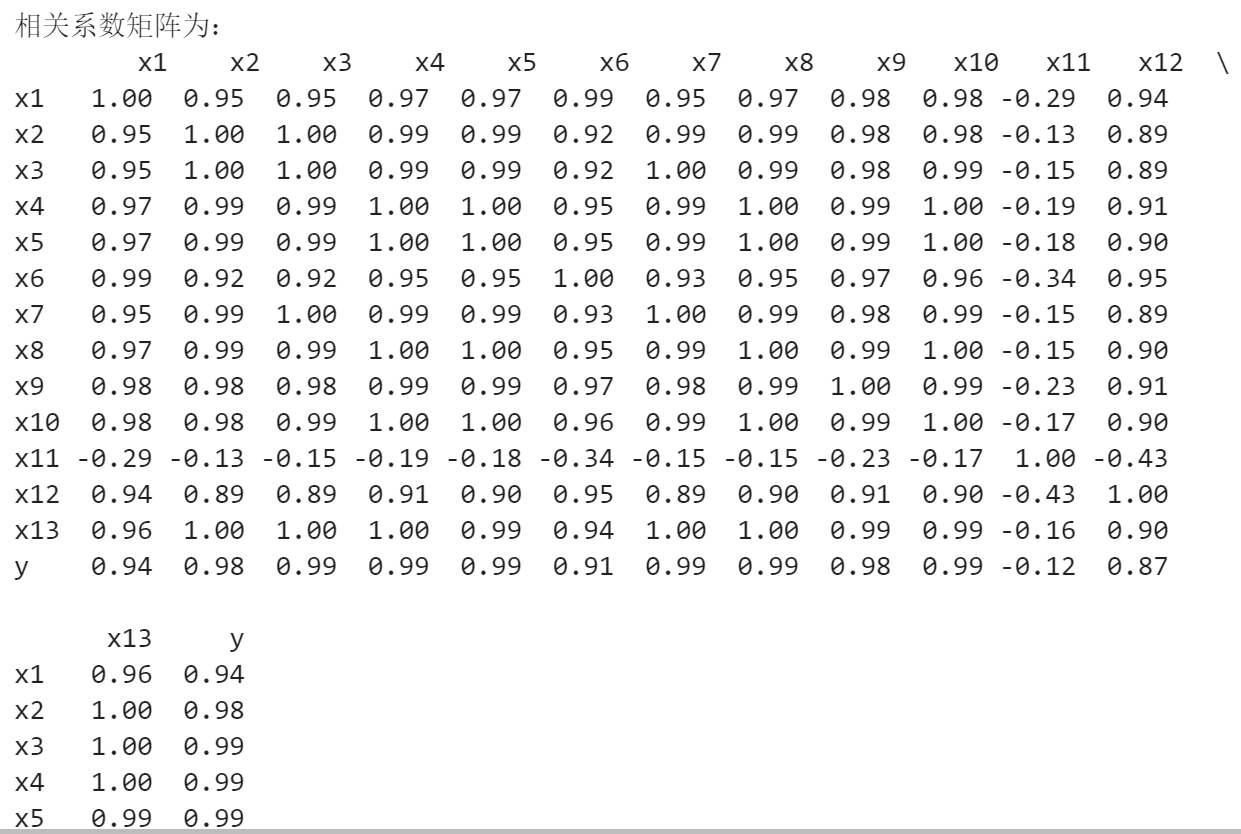
import numpy as np
import pandas as pd
from sklearn.linear_model import Lasso

inputfile="D:\数据分析\data.csv"
data=pd.read_csv(inputfile)
lasso=Lasso(1000)
lasso.fit(data.iloc[:,0:13],data['y'])
print('相关系数为:',np.round(lasso.coef_,5))

print('相关系数非零个数为：',np.sum(lasso.coef_ !=0))
mask=lasso.coef_ !=0
print('相关系数是否为零:',mask)

outputfile="D:/数据分析/new_reg_data.csv"
mask=np.append(mask,True)
new_reg_data=data.iloc[:,mask]
new_reg_data.to_csv(outputfile)
print('输出数据的维度为:',new_reg_data.shape)

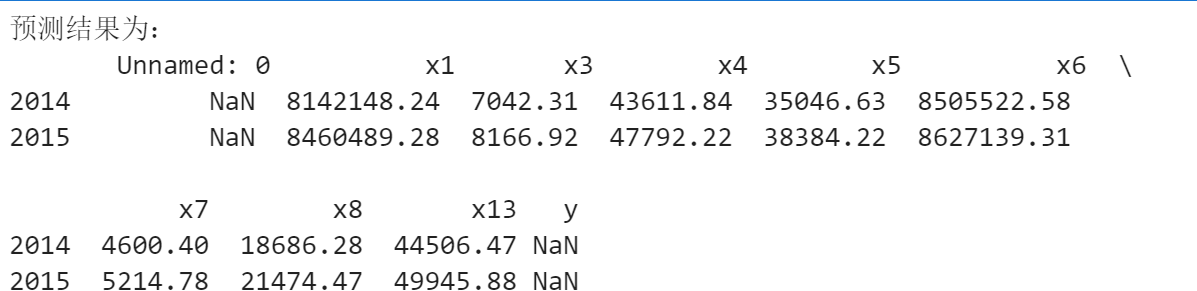
import sys
sys.path.append("D:\数据分析\demo\code")
import numpy as np
import pandas as pd
from GM11 import GM11

inputfile1="D:/数据分析/new_reg_data.csv"
inputfile2="D:/数据分析/data.csv"
new_reg_data=pd.read_csv(inputfile1)
data=pd.read_csv(inputfile2)
new_reg_data.index=range(1994,2014)
new_reg_data.loc[2014]=None
new_reg_data.loc[2015]=None
cols=['x1','x3','x4','x5','x6','x7','x8','x13']
for i in cols:
    f=GM11(new_reg_data.loc[range(1994,2014),i].to_numpy())[0]
    new_reg_data.loc[2014,i]=f(len(new_reg_data)-1)
    new_reg_data.loc[2015,i]=f(len(new_reg_data))
    new_reg_data[i]=new_reg_data[i].round(2)
outputfile="D:/数据分析/new_reg_data_GM11.xls"
y=list(data['y'].values)
y.extend([np.nan,np.nan])
new_reg_data['y']=y
new_reg_data.to_excel(outputfile)
print('预测结果为：\n',new_reg_data.loc[2014:2015:])

 

 

from sklearn.decomposition import PCA
D=np.random.rand(10,4)
pca=PCA()
pca.fit(D)
pca.components_
pca.explained_variance_ratio_

 

 

import numpy as np
import random 
import matplotlib.pyplot as plt 

def distance(point1, point2):  # 计算距离（欧几里得距离）
    return np.sqrt(np.sum((point1 - point2) ** 2))

def k_means(data, k, max_iter=10000):
    centers = {}  # 初始聚类中心
    # 初始化，随机选k个样本作为初始聚类中心。 random.sample(): 随机不重复抽取k个值
    n_data = data.shape[0]   # 样本个数
    for idx, i in enumerate(random.sample(range(n_data), k)):
        # idx取值范围[0, k-1]，代表第几个聚类中心;  data[i]为随机选取的样本作为聚类中心
        centers[idx] = data[i] 
    # 开始迭代
    for i in range(max_iter):  # 迭代次数
        print("开始第{}次迭代".format(i+1))
        clusters = {}    # 聚类结果，聚类中心的索引idx -> [样本集合]
        for j in range(k):  # 初始化为空列表
            clusters[j] = []
            
        for sample in data:  # 遍历每个样本
            distances = []  # 计算该样本到每个聚类中心的距离 (只会有k个元素)
            for c in centers:  # 遍历每个聚类中心
                # 添加该样本点到聚类中心的距离
                distances.append(distance(sample, centers[c])) 
            idx = np.argmin(distances)  # 最小距离的索引
            clusters[idx].append(sample)   # 将该样本添加到第idx个聚类中心
            
        pre_centers = centers.copy()  # 记录之前的聚类中心点

        for c in clusters.keys():
            # 重新计算中心点（计算该聚类中心的所有样本的均值）
            centers[c] = np.mean(clusters[c], axis=0)
        is_convergent = True
        for c in centers:
            if distance(pre_centers[c], centers[c]) > 1e-8:  # 中心点是否变化
                is_convergent = False
                break
        if is_convergent == True:  
            # 如果新旧聚类中心不变，则迭代停止
            break
    return centers, clusters

def predict(p_data, centers):  # 预测新样本点所在的类
    # 计算p_data 到每个聚类中心的距离，然后返回距离最小所在的聚类。
    distances = [distance(p_data, centers[c]) for c in centers]  
    return np.argmin(distances)

x=np.random.randint(0,high=10,size=(200,2))
centers,clusters=k_means(x,3)

 

 

print(centers)
clusters

 

 

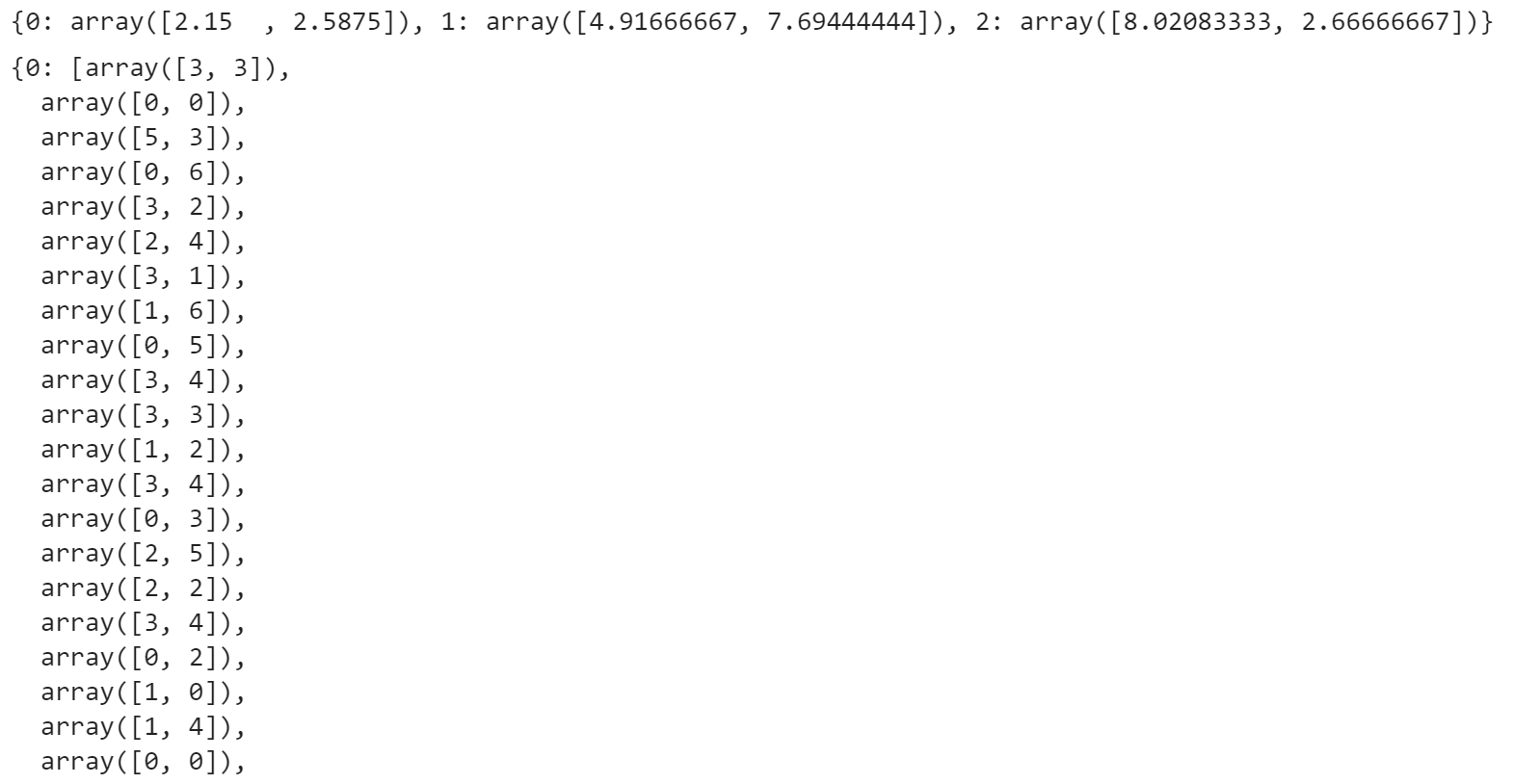
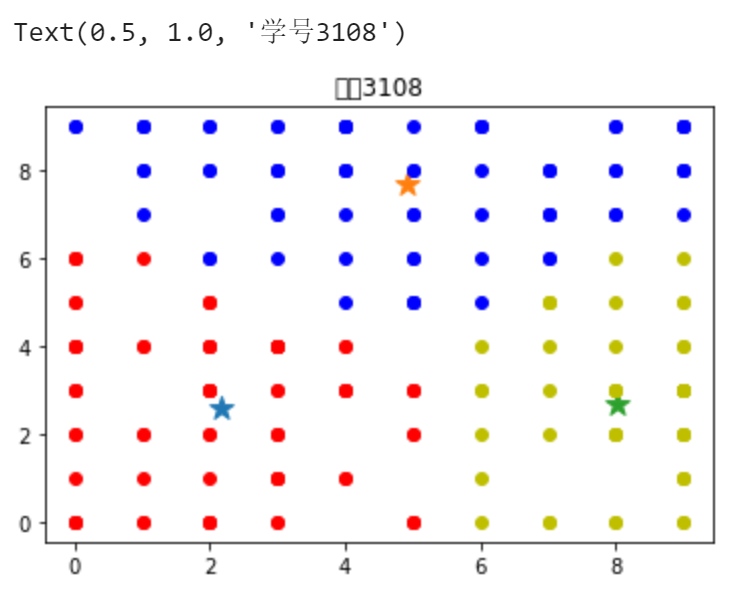
for center in centers:
    plt.scatter(centers[center][0],centers[center][1],marker='*',s=150)
colors=['r','b','y','m','c','q']
for c in clusters:
    for point in clusters[c]:
        plt.scatter(point[0],point[1],c=colors[c])
plt.title('学号3108')

 

 

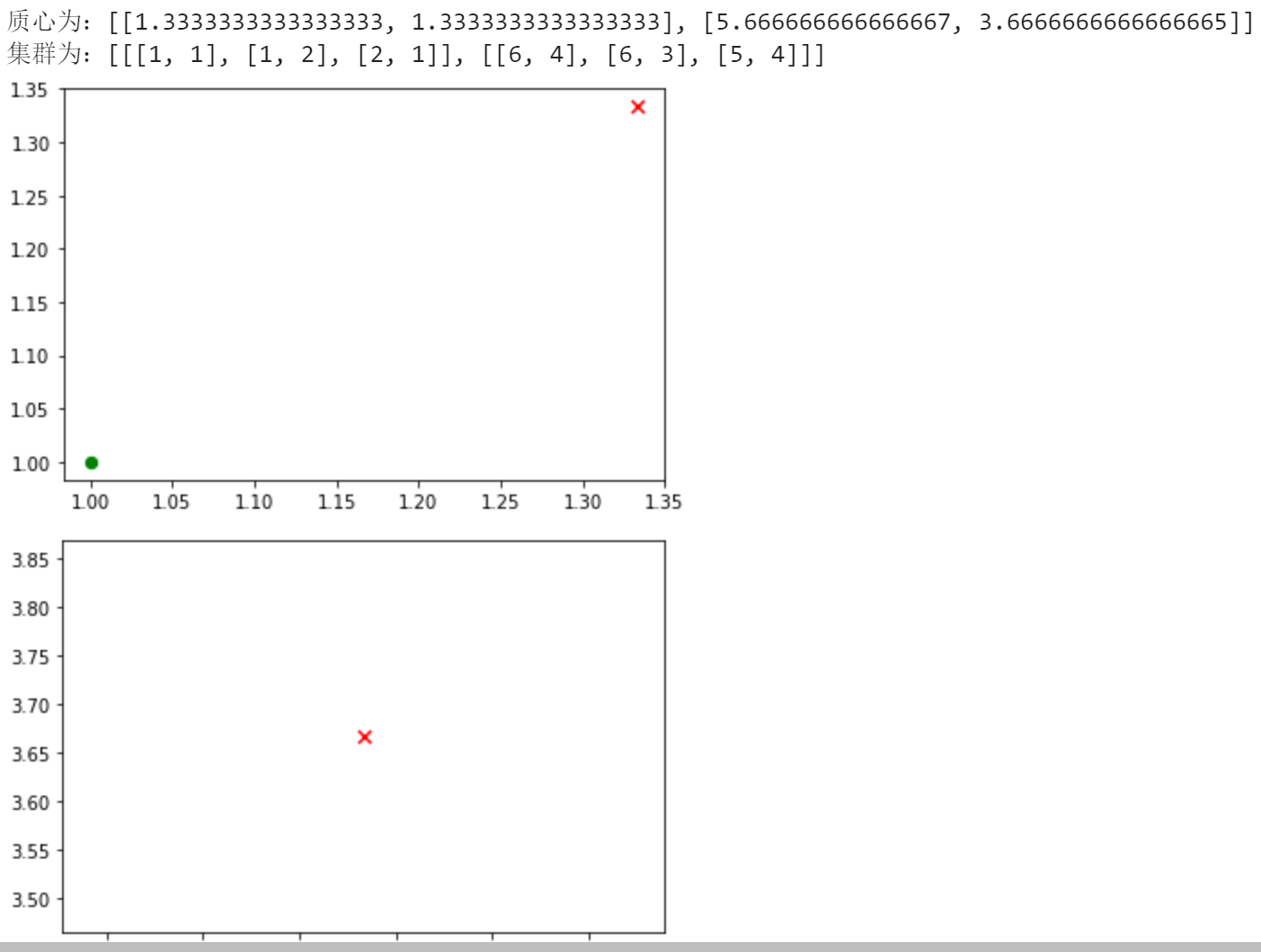
import random
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# 计算欧拉距离
def calcDis(dataSet, centroids, k):
    clalist=[]
    for data in dataSet:
        diff = np.tile(data, (k, 1)) - centroids  #相减   (np.tile(a,(2,1))就是把a先沿x轴复制1倍，即没有复制，仍然是 [0,1,2]。 再把结果沿y方向复制2倍得到array([[0,1,2],[0,1,2]]))
        squaredDiff = diff ** 2     #平方
        squaredDist = np.sum(squaredDiff, axis=1)   #和  (axis=1表示行)
        distance = squaredDist ** 0.5  #开根号
        clalist.append(distance) 
    clalist = np.array(clalist)  #返回一个每个点到质点的距离len(dateSet)*k的数组
    return clalist

# 计算质心
def classify(dataSet, centroids, k):
    # 计算样本到质心的距离
    clalist = calcDis(dataSet, centroids, k)
    # 分组并计算新的质心
    minDistIndices = np.argmin(clalist, axis=1)    #axis=1 表示求出每行的最小值的下标
    newCentroids = pd.DataFrame(dataSet).groupby(minDistIndices).mean() #DataFramte(dataSet)对DataSet分组，groupby(min)按照min进行统计分类，mean()对分类结果求均值
    newCentroids = newCentroids.values
 
    # 计算变化量
    changed = newCentroids - centroids
 
    return changed, newCentroids

# 使用k-means分类
def kmeans(dataSet, k):
    # 随机取质心
    centroids = random.sample(dataSet, k)
    
    # 更新质心 直到变化量全为0
    changed, newCentroids = classify(dataSet, centroids, k)
    while np.any(changed != 0):
        changed, newCentroids = classify(dataSet, newCentroids, k)
 
    centroids = sorted(newCentroids.tolist())   #tolist()将矩阵转换成列表 sorted()排序
 
    # 根据质心计算每个集群
    cluster = []
    clalist = calcDis(dataSet, centroids, k) #调用欧拉距离
    minDistIndices = np.argmin(clalist, axis=1)  
    for i in range(k):
        cluster.append([])
    for i, j in enumerate(minDistIndices):   #enymerate()可同时遍历索引和遍历元素
        cluster[j].append(dataSet[i])
        
    return centroids, cluster
 
# 创建数据集
def createDataSet():
    return [[1, 1], [1, 2], [2, 1], [6, 4], [6, 3], [5, 4]]

if __name__=='__main__': 
    dataset = createDataSet()
    centroids, cluster = kmeans(dataset, 2)
    print('质心为：%s' % centroids)
    print('集群为：%s' % cluster)
    for i in range(len(dataset)):
        plt.scatter(dataset[i][0],dataset[i][1], marker = 'o',color = 'green', s = 40 ,label = '原始点')
                                                    #  记号形状       颜色      点的大小      设置标签
        for j in range(len(centroids)):
        plt.scatter(centroids[j][0],centroids[j][1],marker='x',color='red',s=50,label='质心')
        plt.show()
        plt.title('xuehao3108')

 

 

 

 

2016年：

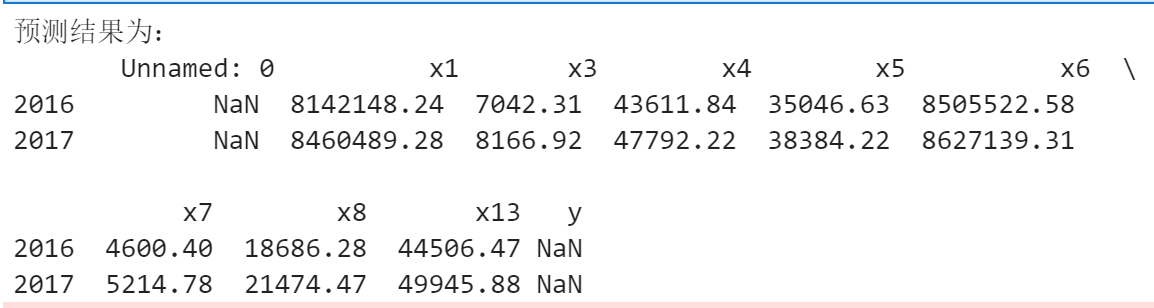
import sys
sys.path.append("D:\数据分析\demo\code")
import numpy as np
import pandas as pd
from GM11 import GM11

inputfile1="D:/数据分析/new_reg_data.csv"
inputfile2="D:/数据分析/data.csv"
new_reg_data=pd.read_csv(inputfile1)
data=pd.read_csv(inputfile2)
new_reg_data.index=range(1996,2016)
new_reg_data.loc[2016]=None
new_reg_data.loc[2017]=None
cols=['x1','x3','x4','x5','x6','x7','x8','x13']
for i in cols:
    f=GM11(new_reg_data.loc[range(1996,2016),i].to_numpy())[0]
    new_reg_data.loc[2016,i]=f(len(new_reg_data)-1)
    new_reg_data.loc[2017,i]=f(len(new_reg_data))
    new_reg_data[i]=new_reg_data[i].round(2)
outputfile="D:/数据分析/new_reg_data_GM110.xls"
y=list(data['y'].values)
y.extend([np.nan,np.nan])
new_reg_data['y']=y
new_reg_data.to_excel(outputfile)
print('预测结果为：\n',new_reg_data.loc[2016:2017:])

 

 

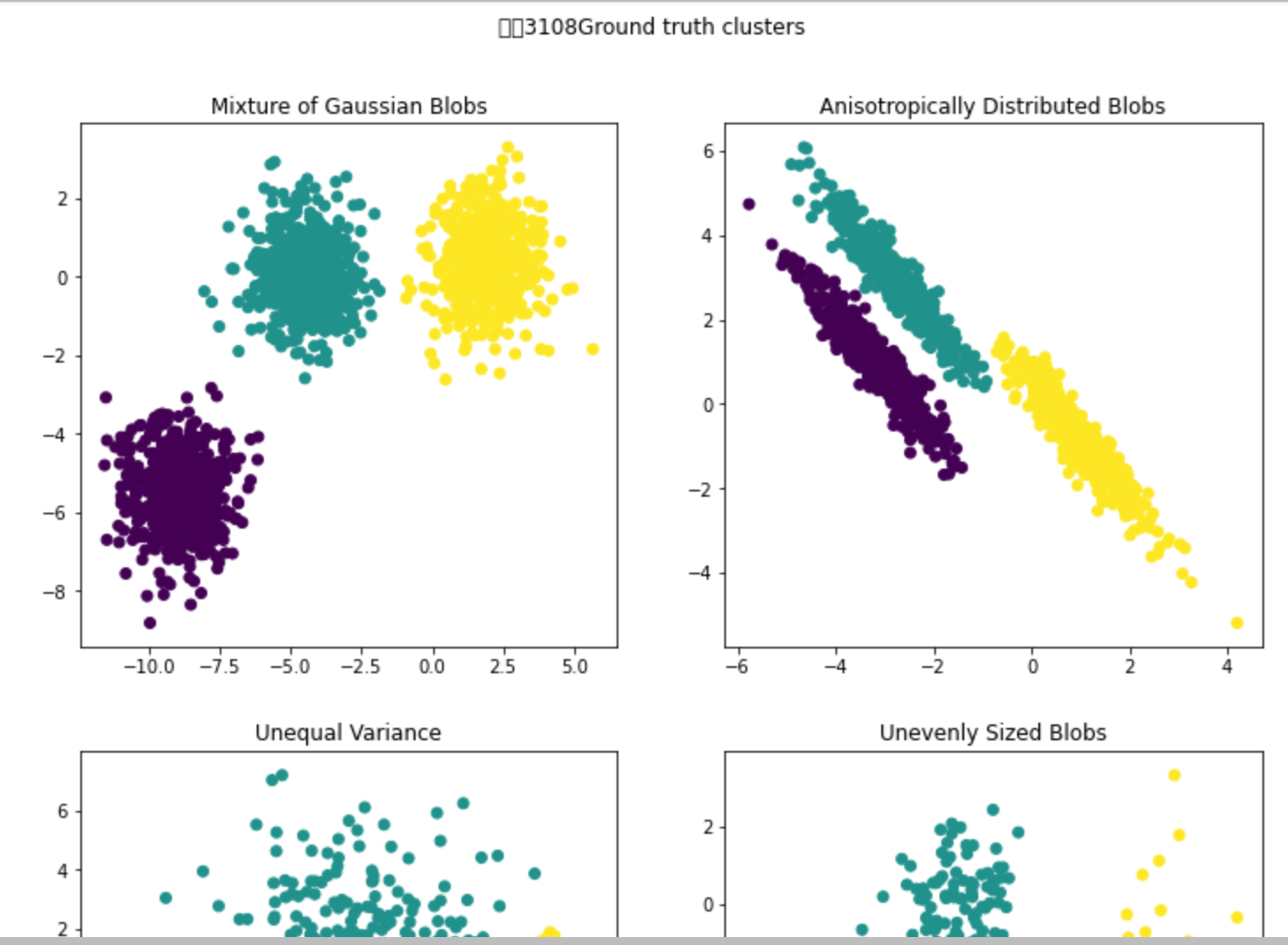
import numpy as np
from sklearn.datasets import make_blobs

n_samples = 1500
random_state = 170
transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]

X, y = make_blobs(n_samples=n_samples, random_state=random_state)
X_aniso = np.dot(X, transformation)  # Anisotropic blobs
X_varied, y_varied = make_blobs(
    n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5], random_state=random_state
)  # Unequal variance
X_filtered = np.vstack(
    (X[y == 0][:500], X[y == 1][:100], X[y == 2][:10])
)  # Unevenly sized blobs
y_filtered = [0] * 500 + [1] * 100 + [2] * 10

import matplotlib.pyplot as plt

fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(12, 12))

axs[0, 0].scatter(X[:, 0], X[:, 1], c=y)
axs[0, 0].set_title("Mixture of Gaussian Blobs")

axs[0, 1].scatter(X_aniso[:, 0], X_aniso[:, 1], c=y)
axs[0, 1].set_title("Anisotropically Distributed Blobs")

axs[1, 0].scatter(X_varied[:, 0], X_varied[:, 1], c=y_varied)
axs[1, 0].set_title("Unequal Variance")

axs[1, 1].scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_filtered)
axs[1, 1].set_title("Unevenly Sized Blobs")

plt.suptitle("学号3108Ground truth clusters").set_y(0.95)
plt.show()