131. 分割回文串(dp+回溯)

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

回文串 是正着读和反着读都一样的字符串。

 

示例 1：

输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]
示例 2：

输入：s = "a"
输出：[["a"]]

回溯的题，至于判断是不是回文串，我主要是有两种方式

1.在遍历的时候搜(用双指针只要O(N)即可)

/* 每次要判断 不太好， 不如一次预处理了 放表格里
    bool check(int start, int end, string & str){
        while(start < end){
            if(str[start] != str[end]){
                return false; 
            }
            start++;
            end--;
        }
        return true;
    }
    */

 

2.用动态规划预处理(O(N²))

这里把所有处理完的数据存在二维数组中，这样后续在用的时候就可以用f[x][y]来表示一个string是不是回文串了，可以节省O(N)的时间

 写出动态方程：

设 f(i, j)f(i,j) 表示 s[i..j]s[i..j] 是否为回文串，那么有状态转移方程：

 

 

f[i][j] = (f[i + 1][j - 1] && s[i] == s[j])

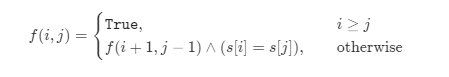
​其中^表示逻辑与运算，即 s[i..j]s[i..j] 为回文串，当且仅当其为空串（i > j），其长度为 1(i=j)，或者首尾字符相同且 s[i+1..j−1] 为回文串。

预处理完成之后，我们只需要O(1) 的时间就可以判断任意 s[i..j] 是否为回文串了。

 动态规划又称表格法,从动态方程看我们是从i + 1 -> i, j - 1 -> j

同时有i < j,所以在循环的时候i应该是从n - 1 -> 0,j应该是从i + 1 -> n

所以预处理主要如下：

    int num = s.size();
    f.assign(num + 1 ,vector<bool>(num + 1,true));
    // f[i][j] = (f[i + 1][j - 1] && s[i] == s[j])
    for(int i = num - 1; i >= 0; i--){
         for(int j = i + 1; j < num; j++){
             f[i][j] = (f[i + 1][j - 1] && s[i] == s[j]);
         }
    }
            

是否是回文串的问题解决了，现在要解决回溯的问题了。

本题的递归树如下所示：

 

 

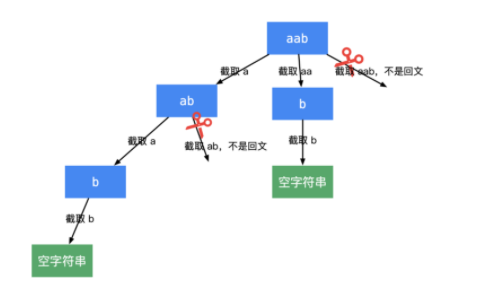
class Solution {
public:
    vector<vector<string>> res;
    vector<vector<bool>> f;
    vector<vector<string>> partition(string s) {
        int num = s.size();
        f.assign(num + 1 ,vector<bool>(num + 1,true));
        // f[i][j] = (f[i + 1][j - 1] && s[i] == s[j])
        for(int i = num - 1; i >= 0; i--){
            for(int j = i + 1; j < num; j++){
                f[i][j] = (f[i + 1][j - 1] && s[i] == s[j]);
            }
        }
        vector<string> temp;
        dfs(0,s,temp);
        return res;
    }
    void dfs(int start, string &str,vector<string> &temp){
        int n = str.size();
        if(start == n){
            res.push_back(temp);
            return;
        }
        for(int i = start; i < n; i++){
            if(f[start][i]){
                temp.push_back(str.substr(start,i - start + 1));
                dfs(i + 1,str,temp);
                temp.pop_back();
            }
        }
    }

 

回溯主要是要注意以下几个点：

1.传入参数应该是什么？

这题首先要记住开始的start，然后对从i从start到length(字符串长度)进行回文串的判断，如果不是回文串，就进行i + 1的操作，如果是回文串，就进行start = i + 1的递归。

所以传入参数必要的有index，和string，由于在访问到最后我们还需要保存一个vector<string> 类型的数组，所以还需要传入一个vector<string>类型的数组。

2.结束的条件(这里不是递归结束的条件，而且回溯的条件）

每当访问到start == n的时候，说明满足了符合条件的分割，用一个字符串数组temp存储下来，然后进行回溯的操作。

回溯的时候记得进行temp.pop_back()的操作(因为之前已经保存了一个有用的回文串到temp中，而回溯后不再需要了)