B树

前言：在前面介绍的二叉排序树和平衡树中，每个结点最多只有两棵子树，每个结点只有一个索引。而在下面我们介绍的B树中，每个结点可以有多棵子树，每个结点可以有多个索引。

B树，又称多路平衡查找树，B树种所有结点的孩子结点数的最大值称为B树的阶。

注意：B树也是查找树，树中的元素是排列顺序的。

　　一棵m阶B树或为空树，或为满足如下特性的m叉树：

　　1.数中每个结点至多有m棵子树（至多含有m-1个关键字）

　　2.若根结点不是终端结点，则至少有两棵子树

　　3.除根结点外的所有非叶结点至少有棵子树（即个关键字）

　　4.非叶结点的结构：

n

P0

K1

P1

K2

P2

...

Kn

Pn

　　Ki(i=1, 2, ..., n)为结点的关键字， K1 < K2 < ... < Kn，即满足递增顺序。

　　Pi(i=0, 1, 2, ..., n)为子树根结点的指针。Pi-1所指子树的关键字均小于Ki，Pi所指子树的关键字均大于Ki。

　　5.所有的叶结点都出现在同一层次上，并不带任何信息。

 

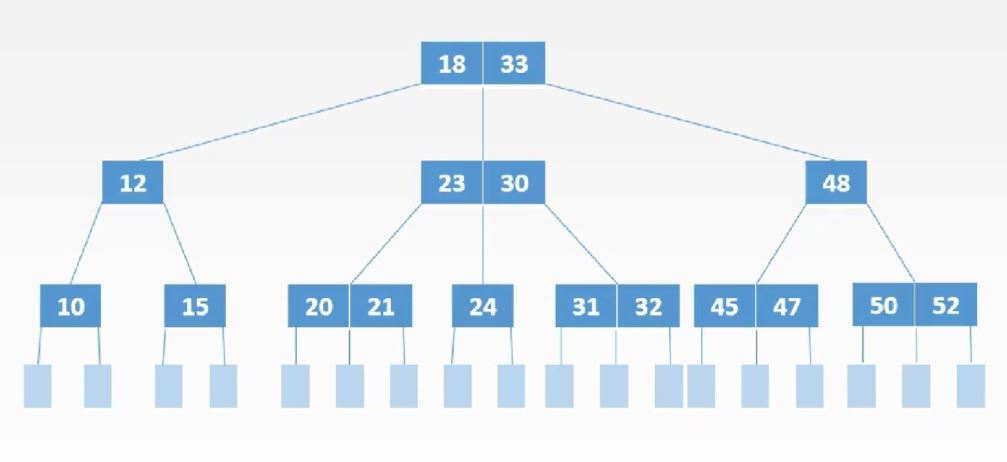
n个关键字，阶数为m，高度为h的B树

　

 

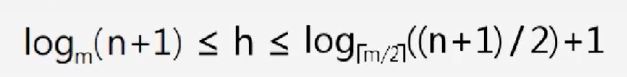
查找

1.在B树中查找存放该关键字的结点。

2.在该结点中查找关键字（结点中的关键字是按照顺序排列的，可以很方便的查找）。

 

插入

1.定位：定位到我们需要插入的结点

　　查找插入该关键字的位置，即最底层中的某个非叶子结点（规定一定是插入在最底层的某个非叶子结点内）

2.插入：

　　若插入后，不会破坏m阶二叉树的定义，即插入后结点的关键字个数在区间，则直接插入。

 

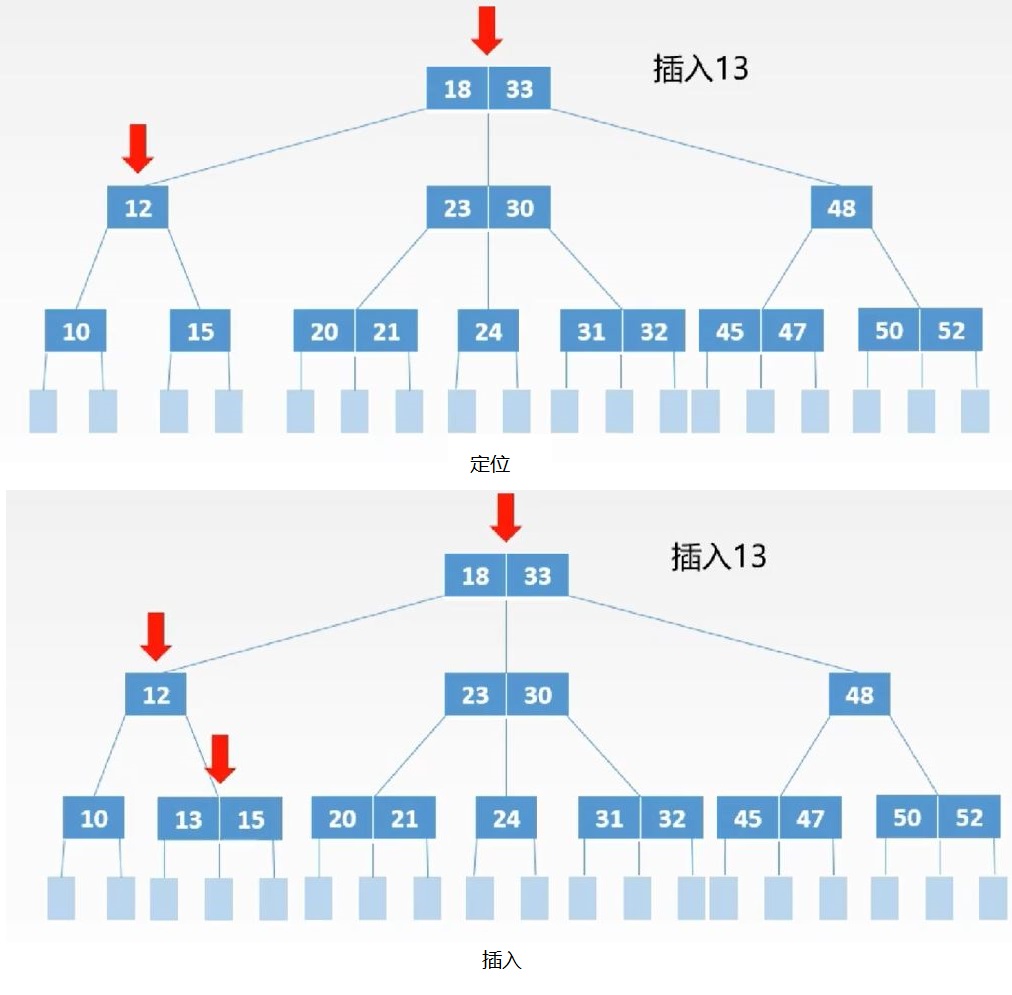
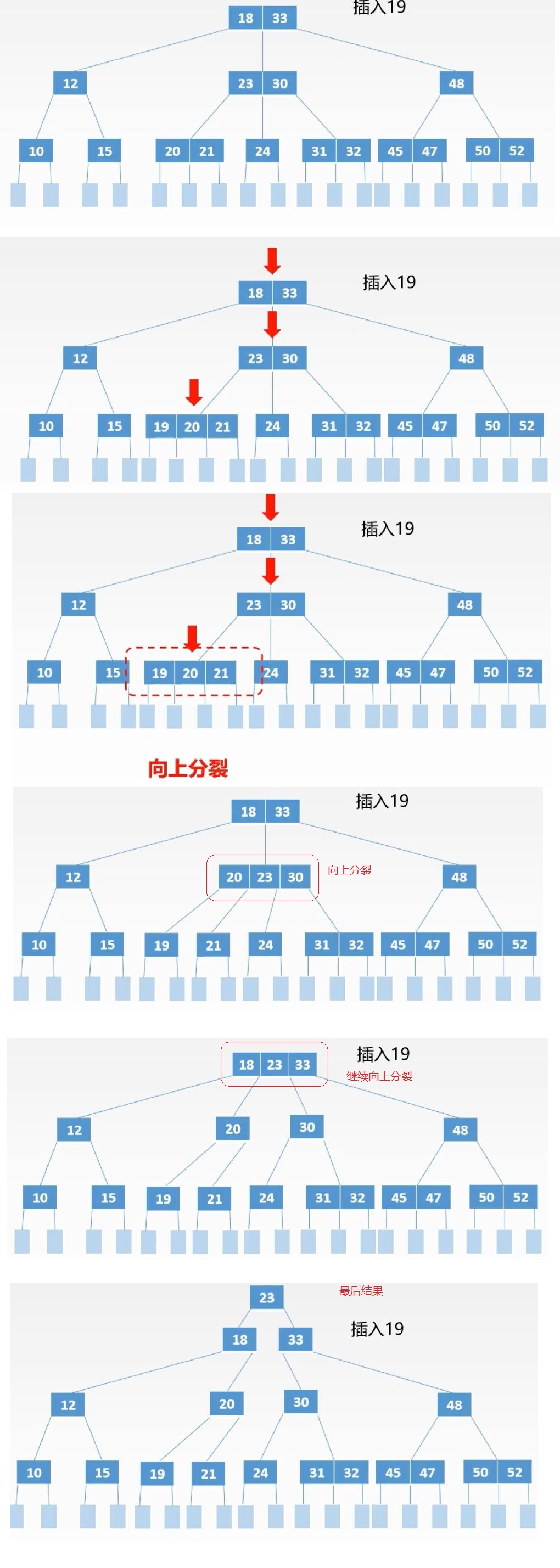
　　若插入后，关键字数量大于m-1,则对插入后的结点进行分裂操作。

　　分裂：1.插入后的结点中间位置（）关键字并入父结点中；2.中间节点左侧结点留在原先的位置中，右侧结点放入新的结点中；3.若并入父结点后，父结点关键字数量超出范围，继续向上分裂，直至符合要求为止。

　　若分裂到根结点之后，仍然超出关键字数量范围，那么则继续向上分裂，使整棵B树的高度加1。

 

 删除操作

删除操作分为终端结点和非终端结点两种情况进行。

对终端结点的删除操作

1.直接删除

　　若被删除关键字所在结点关键字个数大于，表明删除后仍满足B树定义，直接删除。

2.兄弟够借

　　若被删除关键字所在结点关键字总数等于，且与此结点邻近的兄弟结点的关键字个数不小于，则需要从兄弟结点借一个关键字，此过程需要调整该节点、双亲结点和兄弟结点的关键字。

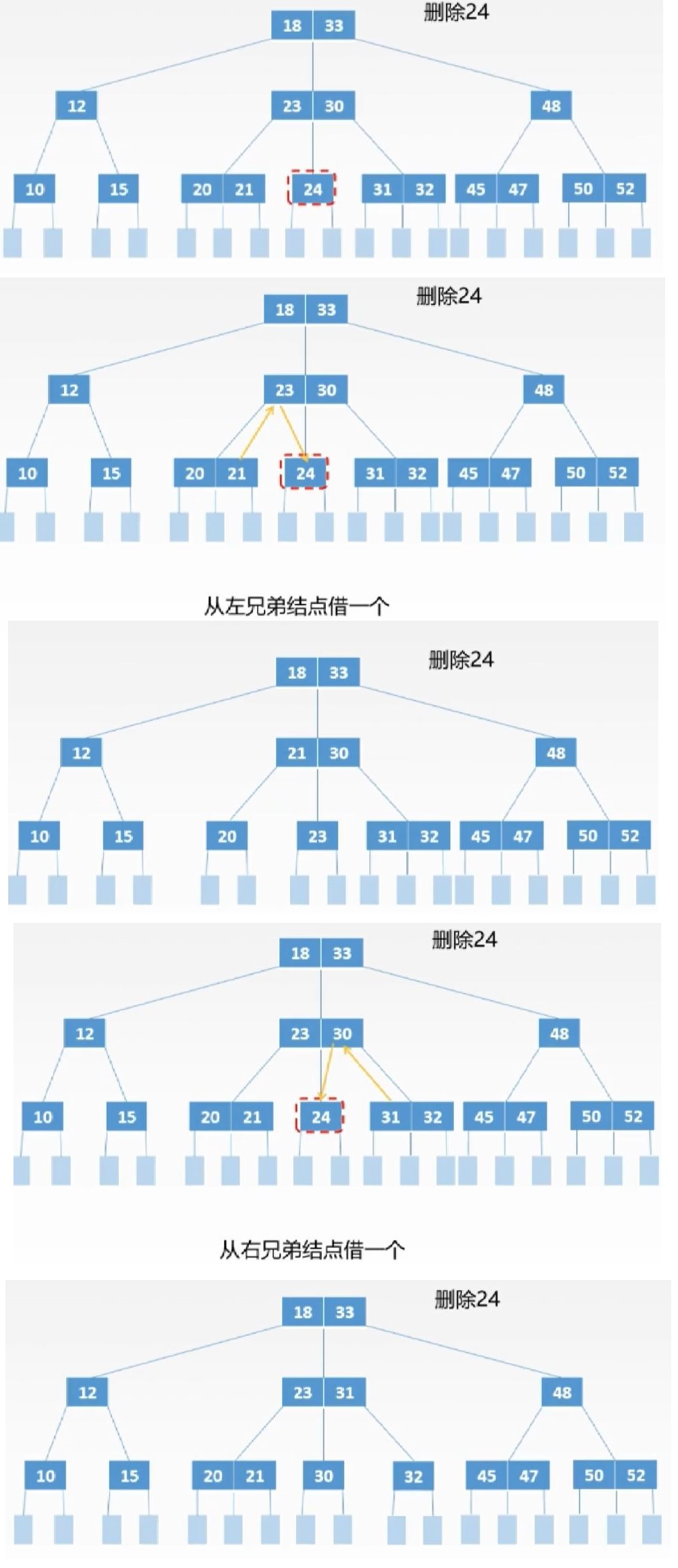
3.兄弟不够借

若被删除关键字所在结点关键字总数为，且与此结点邻近的兄弟结点的关键字个数为，则删除关键字，并将一个不够借的兄弟结点和双亲结点中两兄弟子树中间的关键字合并。

若合并后双亲结点因减少一个结点导致不符合定义，则继续执行2、3步骤。

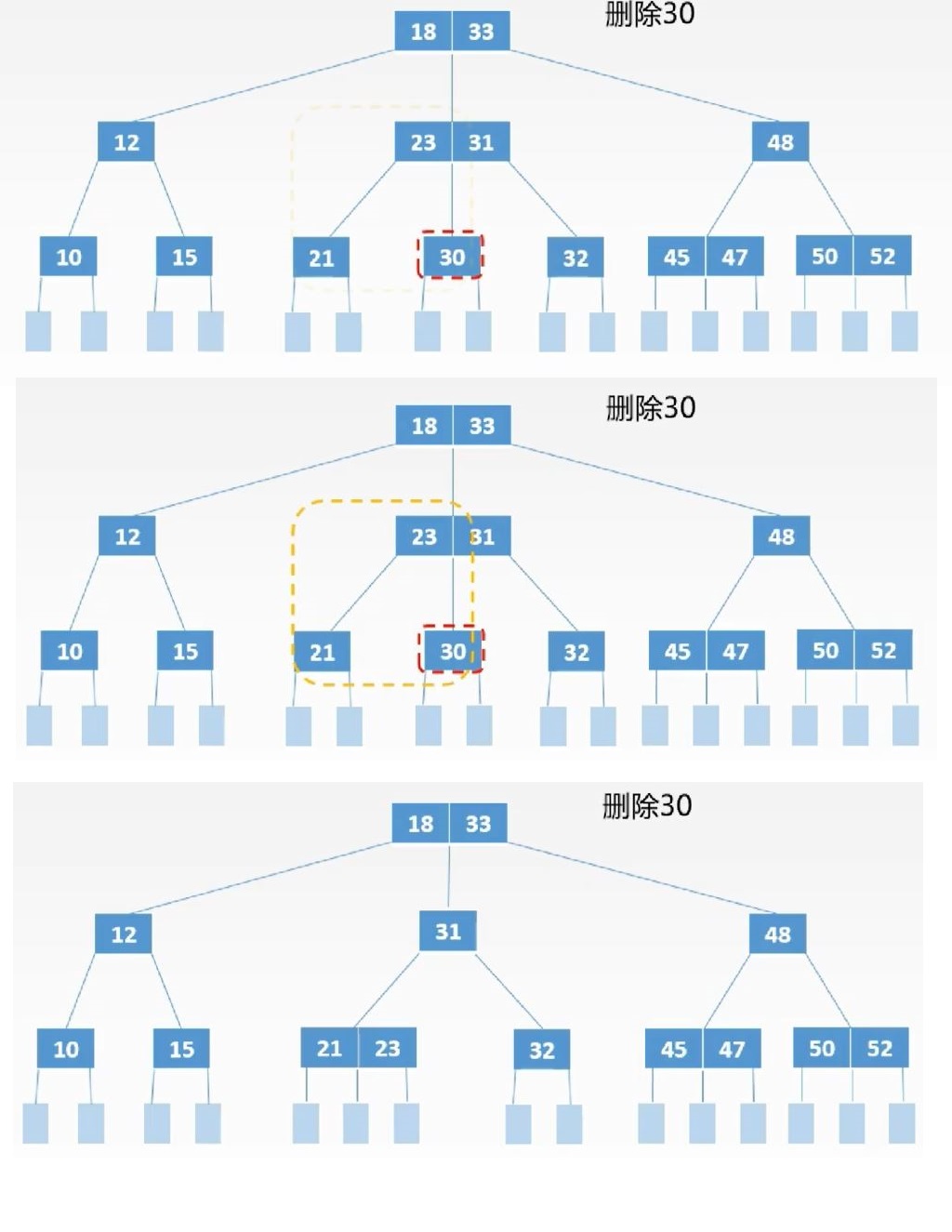
 删除非终端结点

　　1.若小于k的子树中关键字个数>,则找出k的前驱值k'，并用k'来代替k，再递归删除k'即可

　　前驱值：所有数按照从小达到顺序排列之后，在比k小的数中最大的那个数，在树中就是k左边的子树当中最右侧的那个值。

 

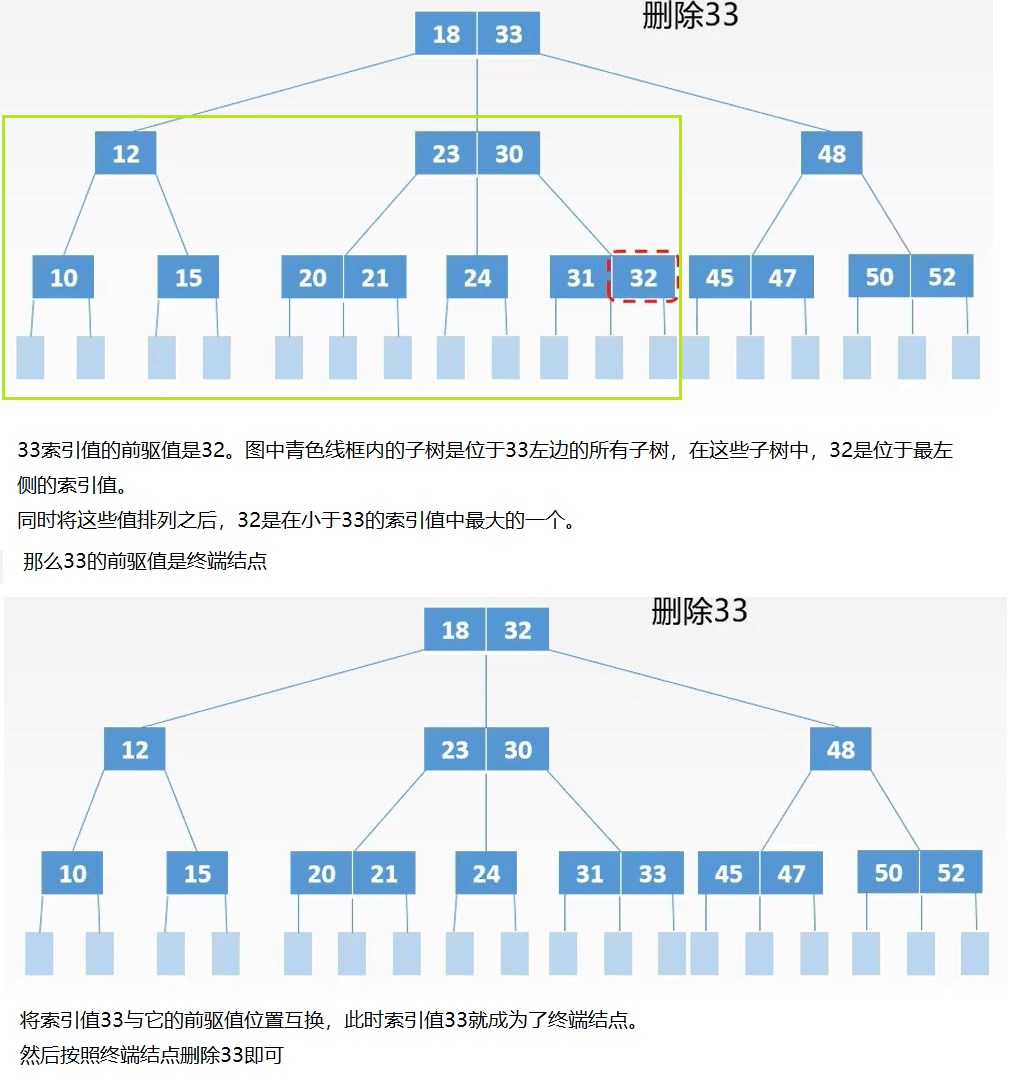
　　2.若大于k的子树中关键字个数>,则找出k的后继值k'，并用k'来代替k，再递归删除k'即可

　　过程如上图所示，只不过结点33的后继结点是45。

　　3.若前后两子树关键字个数均为,则直接将两个子节点合并，然后删除k即可

 

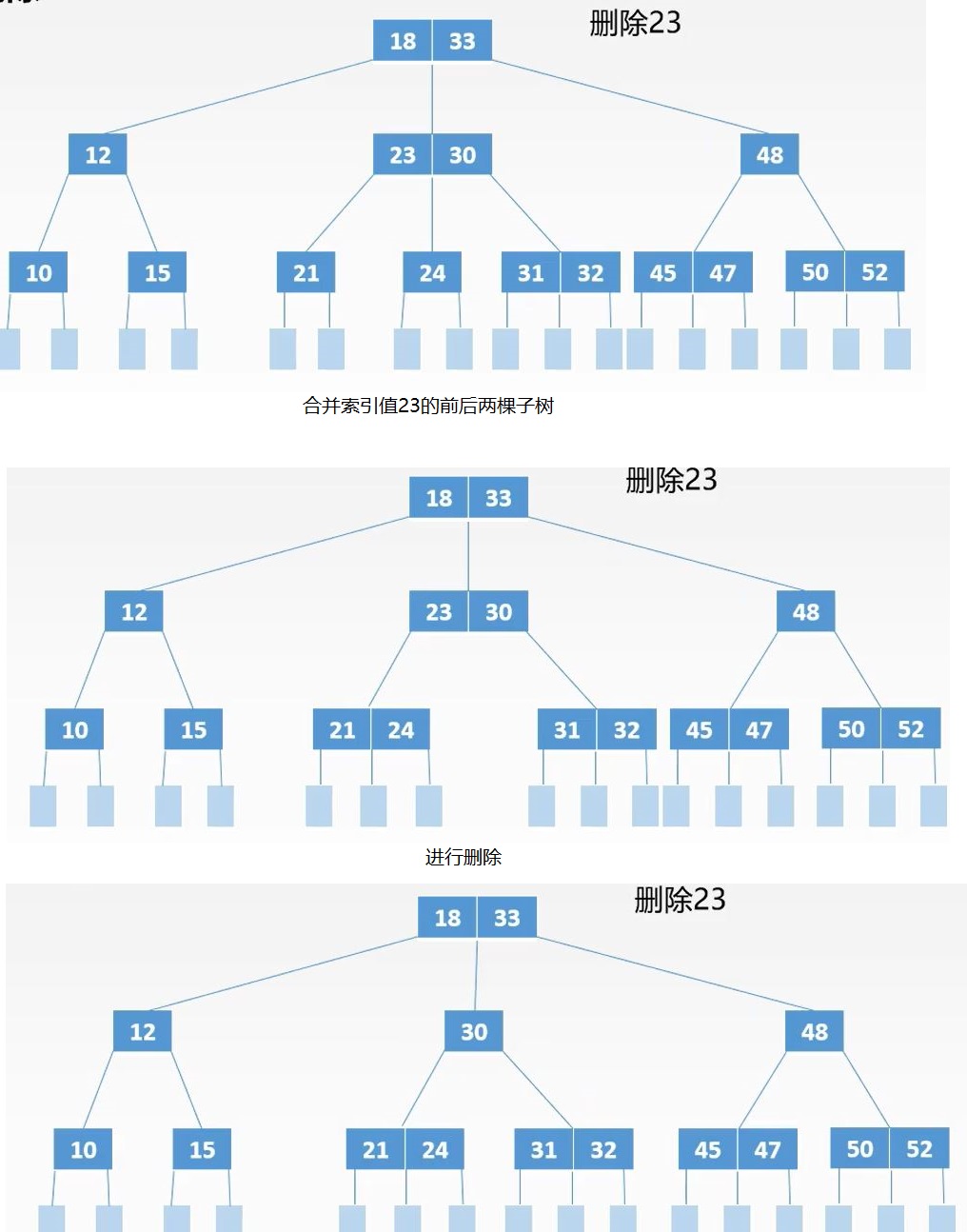
B+树

一棵m阶B+树满足如下特性：

　　1.数中每个结点至多有m棵子树（至多含有m-1个关键字）

　　2.若根结点不是终端结点，则至少有两棵子树

　　3.除根结点外的所有非叶结点至少有棵子树，子树和关键字个数相等

　　4.所有叶结点包含全部关键字及指向相应记录的指针，叶结点中将关键字按照哦从小到大顺序排列，并且相邻结点按照大小顺序连接起来。

　　5.所有分支结点（可视为索引的索引）中仅包含它的各个子结点（下一级索引块）中关键字的最大值及指向其子结点的指针。

 

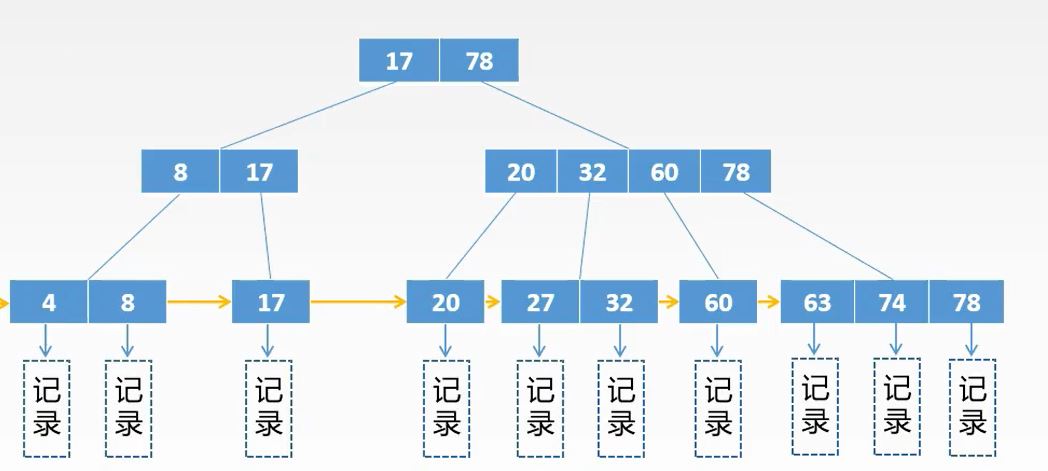
由B+树的性质可知，B+树不仅可以从终端结点按照多路查找，也可以从叶结点逐一顺序查找。

在B+树中查找时，无论成功还是失败一定是查找到叶结点当中的值为止。