CRT && exCRT模板
CRT从各种方面上都吊打exCRT啊......
短,好理解...
考虑构造bi使得bi % pi = ai,bi % pj = 0。然后全加起来就行了。
显然bi的构造就是ai * (P/pi) * inv(P/pi)。
LL a = 0, p = MO - 1; for(int i = 1; i <= 4; i++) { a = (a + ans[i] * (p / mod[i]) % p * qpow(p / mod[i], mod[i] - 2, mod[i]) % p) % p; }
exCRT:
是这样的,重新手推了一个短一点的模板。题是洛谷P3868 猜数字
1 inline int exCRT(int n, int *a, int *b) { 2 int t = a[1], p = b[1], x, y; 3 for(int i = 2; i <= n; i++) { 4 int g = exgcd(p, b[i], x, y); 5 p = lcm(p, b[i]); 6 t = (t - a[i]) % p; 7 y = y * (t / g) % p; 8 t = (a[i] + y * b[i]) % p; 9 } 10 return t; 11 }
具体操作的时候开long long,龟速乘,记得全程避免负数。
先背为敬。

1 #include <cstdio> 2 #include <algorithm> 3 4 typedef long long LL; 5 const int N = 100010; 6 7 LL p[N], a[N]; 8 9 inline LL mod(LL a, LL c) { 10 if(c < 0) { 11 c = (~c) + 1; 12 } 13 while(a >= c) { 14 a -= c; 15 } 16 while(a < 0) { 17 a += c; 18 } 19 return a; 20 } 21 inline LL mul(LL a, LL b, LL c) { 22 LL ans = 0; 23 while(b) { 24 if(b & 1) { 25 ans = mod(ans + a, c); 26 } 27 a = mod(a << 1, c); 28 b = b >> 1; 29 } 30 return ans; 31 } 32 LL exgcd(LL a, LL b, LL &x, LL &y) { 33 if(!b) { 34 x = 1; 35 y = 0; 36 return a; 37 } 38 LL g = exgcd(b, a % b, x, y); 39 std::swap(x, y); 40 y -= (a / b) * x; 41 return g; 42 } 43 44 int main() { 45 int n; 46 scanf("%d", &n); 47 for(int i = 1; i <= n; i++) { 48 scanf("%lld%lld", &p[i], &a[i]); 49 } 50 51 LL A = a[1], P = p[1]; 52 for(int i = 2; i <= n; i++) { 53 LL x, y; 54 LL C = (a[i] - A), g = exgcd(P, p[i], x, y); 55 C = (C % p[i] + p[i]) % p[i]; 56 if(C % g) { 57 puts("-1"); 58 return 0; 59 } 60 61 x = mul(x, C / g, P / g * p[i]); 62 A += mul(x, P, P / g * p[i]); 63 P *= p[i] / g; 64 A = mod(A, P); 65 } 66 67 // x === A mod P 68 LL x, y; 69 exgcd(P, 1, y, x); 70 x *= A; 71 x = (x % P + P) % P; 72 printf("%lld\n", x); 73 return 0; 74 }
尝试合并两个同余方程:
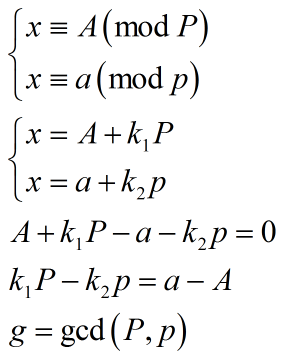
判断有解后可用exgcd解方程。
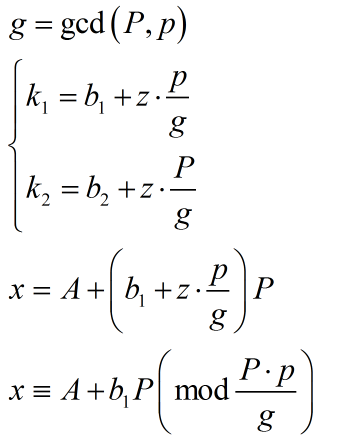
至此合并完成。
所有方程逐一合并即可。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号










