带状对角矩阵压缩算法

首先，要明白的是带状对角矩阵的含义。即所有的非零元素集中在以主对角线为中心的带状区域中，即除了主对角线和主对角线相邻两侧的若干条对角线上的元素之外，其余元素皆为零的矩阵为对角矩阵。

带状矩阵所有非0元素都集中在以主对角线为中心的带状区域，半带宽为d时， 对左上角和右下角进行补“0”，如下图，则非0元素有（2d+1）*n-（1+d）*d个

当|i-j|>1时，元素a[i][j]=0。

 

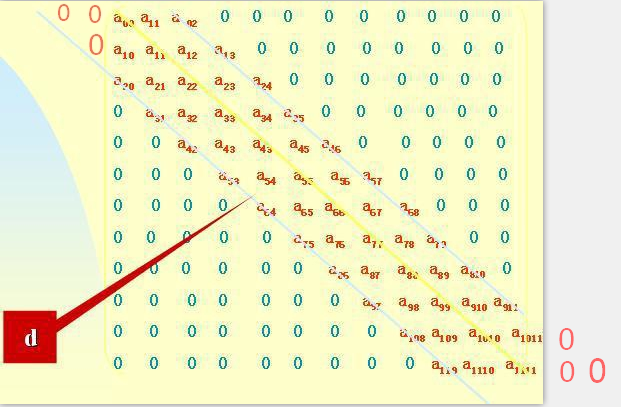
为了节省空间（压缩），用一维数组A[]来存储

k=i*（2d+1）+d+（j-i）（k从0开始）

（i*（2d+1）表示前i行一共有几个元素，而d+（j-i）这一项是用来确定第i行中，第j列前有几个元素，如以i=j为例时，这时j-i=0）

反推公式为

i=k/5

j=k%5