西安电子科技大学week01-状态空间表示及其问题解决

1，盲目搜索

1.1 宽度优先搜索

        基本思想：

• • •  扩展初始节点
    • 扩展初始节点的所有后继节点
    • 扩展后继节点的后继节点
    • 第n层结束，不可能到n+1层

要点:

• • • 新扩展节点放于OPEN表末端
    • 问题有解时，一定可以找到
    • 方法具有通用性
    • 数据规模大时，搜索效率低

1.2 深度优先搜素

基本思想：

• • • 总是扩展当前节点的最深节点
    • 一直扩展直到到达最深层，直至没有下一层
    • 回退到上一个还有未扩展后继节点的上层继续扩展

深度的定义：起始节点深度为0；

                      任何其他节点的深度为d=d(父)+1

要点:

• • • 不能保证最优解
    • 存在无穷分支时可能不能找到解(此时可以借助深度界限解决，一些问题上极为重要)

1.3 等代价搜索

基本思想：属于宽度优先的拓展，此时不沿着等长度路径断层扩展，沿着等代价路径断层扩展

等代价的定义：

• • • g(n)表示从初始节点到当前节点n的代价
    • c(n1，n2)表示从父节点n1到其子节点n2的代价
    • g(n2) = g(n1) + c(n1，n2)

要点：每次扩展代价最低的节点，依据代价对OPEN表中元素进行排序。只有当目标节点位于表中第一个节点时搜索结束。

2，启发式搜索

启发信息：见上图中解释

评估函数：作为启发信息，对当前搜索状态评估，根据函数值对OPEN重排，直接扩展最有希望节点。

              f(n) = g(n) + h(n)

              g(n)表示从起始节点到当前节点的代价

              h(n)表示从当前节点到目标节点的代价

2.1 A算法

局部择优算法(瞎子爬山算法)

•  要点：用f(n)算出每个子节点的估价，根据该估价对OPEN表进行重排，只对扩展节点这一部分重排，估价越小排在越前面。

全局择优算法(全局择优算法)

•  要点：用f(n)算出每个子节点的估价，根据该估价对OPEN表进行重排，对OPEN中所有节点进行重排，估价越小排在越前面。

2.2 A*算法

• 背景：A算法不确定能保证找到最优估价函数，A*算法在A算法的基础上添加一点小改动，使得估价函数能够使最佳，从而找到最佳路径、
• f(n) = g(n) + h(n)

          在A算法的基础上，g(n)>0 , h(n) 是 h*(n) 的下界，即对于任意n , h(n) < =h*(n) , 在满足h(n) < =h*(n)的条件下，h(n) 越大越好。

          h(n) = 0时，则等价为等代价算法。

3，例题理解

宽度优先

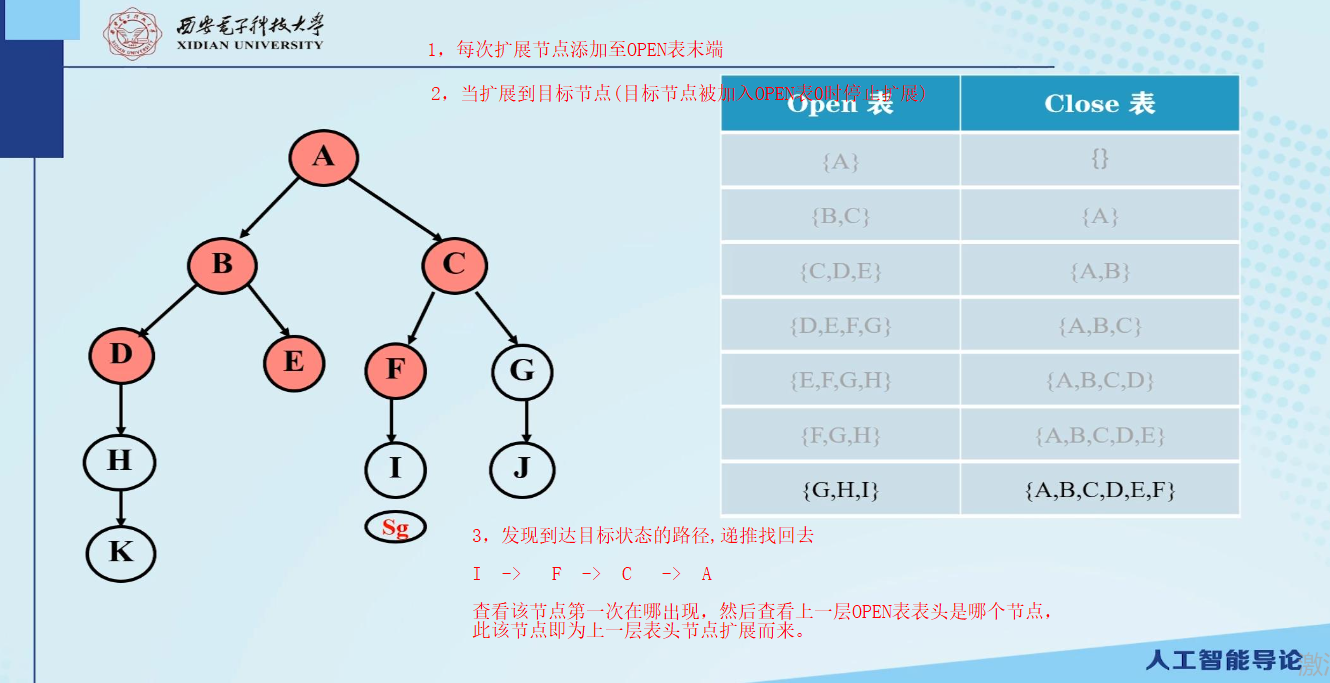
深度优先

 

等代价

启发式搜索可以解决结构比较复杂的问题，不大方便截图