python turtle画汉诺塔移动方法

Turtle库是Python语言中一个很流行的绘制图像的函数库，想象一个小乌龟，在一个横轴为x、纵轴为y的坐标系原点，(0,0)位置开始，它根据一组函数指令的控制，在这个平面坐标系中移动，从而在它爬行的路径上绘制了图形。
设置画布大小

     turtle.screensize(canvwidth=None, canvheight=None, bg=None)，参数分别为画布的宽(单位像素), 高, 背景颜色。

    如：turtle.screensize(800,600, "green")

           turtle.screensize() #返回默认大小(400, 300)

画笔的属性

    画笔(画笔的属性，颜色、画线的宽度等)

    1) turtle.pensize()：设置画笔的宽度；

    2) turtle.pencolor()：没有参数传入，返回当前画笔颜色，传入参数设置画笔颜色，可以是字符串如"green", "red",也可以是RGB 3元组。

    3) turtle.speed(speed)：设置画笔移动速度，画笔绘制的速度范围[0,10]整数，数字越大越快。

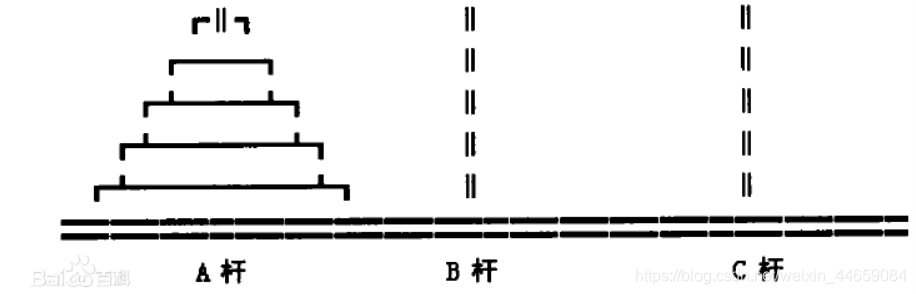
汉诺塔问题：该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘(如下图)。游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

import turtle

class Disk(turtle.Turtle):
    """汉诺塔圆盘类Disk，继承于Turtle"""

    def __init__(self, n):
        """初始化第n个圆盘"""
        turtle.Turtle.__init__(self, shape='square', visible=False) #海龟形状为方形
        self.penup()               # 移动时不绘制轨迹
        self.sety(300)              # 圆盘初始位于圆柱上方
        self.shapesize(1, 1.5*n, 1) # 设置海龟形状（使用不同长度的矩形表示不同圆盘）
        self.fillcolor(1, 1, 1)     # 设置海龟填充色为白色（即圆盘为白色）
        self.showturtle()           # 显示海龟（即圆盘）

class Peg(turtle.Turtle, list):
    """汉诺塔的圆柱类Peg，继承于Turtle和list。"""
    def __init__(self, n, pos):
        """初始化可以容纳n个圆盘的圆柱对象"""
        turtle.Turtle.__init__(self, shape='square',visible=False)
        self.penup()              # 移动时不绘制轨迹
        self.shapesize(n*1.25,.75,1) # 设置海龟形状（使用不同长度的矩形表示不同圆盘）
        self.sety(12.5*n)         # 设置y坐标
        self.x = pos
        self.setx(self.x)         # 设置x坐标
        self.showturtle()         # 显示海龟（即圆柱）

    def push(self, disk):
        """把圆盘disk放置到圆柱上"""
        disk.setx(self.x)         # 设置x坐标
        disk.sety(10+len(self)*25)# 设置y坐标
        self.append(disk)         # 附加到列表中

    def pop(self):
        """从圆柱上移除圆盘并返回圆盘"""
        disk = list.pop(self)     # 从列表中移除圆盘
        disk.sety(300)            # 移除圆盘海龟
        return disk               # 返回圆盘

def move_disk(from_peg, to_peg):
    """把圆柱from_peg上的一个圆盘移动到圆柱to_peg上"""
    disk = from_peg.pop()
    to_peg.push(disk)


def hanoi(n, peg1, peg2, peg3):
    """汉诺塔递归求解，把n个圆盘从peg1移动到peg3（通过peg2）"""

    # 基本情况：n == 0，什么也不做
    # 递归步骤
    if n > 0:
        hanoi(n-1, peg1, peg3, peg2) 
        move_disk(peg1, peg3)
        hanoi(n-1, peg2, peg1, peg3)

def main(n):
    """n个圆盘的汉诺塔递归求解"""
    screen = turtle.Screen() #创建屏幕对象
    p1 = Peg(n, -200) #创建一个可以容纳n个圆盘位于x=-200位置的圆柱
    p2 = Peg(n, 0)  #创建一个可以容纳n个圆盘位于x=200位置的圆柱
    p3 = Peg(n, 200)  #创建一个可以容纳n个圆盘位于x=400位置的圆柱
    for i in range(n): # 创建n个圆盘对象并按从大到小的顺序放置到peg1
        p1.push(Disk(n-i))  
    hanoi(n, p1, p2, p3)
    screen.bye()

if __name__ == '__main__':
   main(3)