机器学习总结之第二章模型评估与选择
【第2章 模型评估与选择】
〖一、知识点归纳〗
一、经验误差与过拟合
【分类】:对是离散值的结果进行预测。
【回归】:对是连续值的结果进行预测。
分类和回归属于监督学习。
【错误率】:分类错误的样本数占样本总数的比例。
eg:m个样本中有a个样本分类错误,则错误率
【精度】:分类正确的样本数占样本总数的比例。即:精度=1-错误率。
eg:m个样本中有m-a个样本分类正确,则精度
【误差】:学习器的实际预测输出与样本的真实输出之间的差异。
eg:1000个西瓜中,好瓜有400个,但学习器预测有500个,这之间的差异就是误差。
【训练误差、经验误差】:学习器在训练集上的误差。
值得一提的事,学习器就是在训练集上训练出来的,但实际上在回到训练集上对样本进行结果预测时,仍有误差。(即结果值和标记值不同)
https://www.quora.com/What-is-a-training-and-test-error
Training error is the error that you get when you run the trained model back on the training data. Remember that this data has already been used to train the model and this necessarily doesn't mean that the model once trained will accurately perform when applied back on the training data itself.
eg:100000个用来得出学习器的西瓜在学习器中进行分类测试,发现有10000个西瓜分类错误。则分类错误率为10%,分类精度为90%
【泛化误差】:学习器在新样本上的误差。
eg:100个新西瓜,使用学习器分类,分类错误的有20个。则分类错误率为20%,精度为80%。
希望:得到泛化误差最小的学习器。
实际能做的:努力使经验误差最小化。
注意:努力使经验误差最小化≠让经验误差达到最小值即训练集的分类错误率为0%。
因为在训练集上表现很好的学习器,泛化能力却并不强。
【过拟合】:学习能力过于强大。学习器把训练样本学得太好,导致将训练样本中自身含有的特点当成所有潜在样本都会具有的一般性质,从而训练后使得泛化性能下降。
eg:100000个用来得出学习器的西瓜都是球形瓜,训练出的决策树判断只有瓜是球形才可能是好瓜,但实际上市场上培养的方形瓜也是好瓜,这就让训练出的决策树在面对方形瓜时的泛化能力变得很差。
【欠拟合】:学习能力底下。对训练样本的一般性质尚未学好。
eg:色泽是判断瓜是否是好瓜的重要标准,但经过训练得到的决策树却没有对色泽进行判断的步骤。
所以实际能做的:努力使经验误差最小化,是指在“过拟合”与“欠拟合”之间寻找一种平衡,并尽可能的使学习器在不太过拟合的情况下使得训练集的分类更准确。
任何学习算法都有针对过拟合的措施,但过拟合是无法完全避免的。
【多项式时间(Polynomial time)】:在计算复杂度理论中,指的是一个问题的计算时间m(n)不大于问题大小n的多项式倍数。任何抽象机器都拥有一复杂度类,此类包括可于此机器以多项式时间求解的问题。
【P问题】:指的是能够在多项式的时间里得到解决的问题。
【NP问题】:指的是能够在多项式的时间里验证一个解是否正确的问题。
【证明过拟合无法避免】:
1.机器学习面临的是一个NP或更难的问题,即∃NP;
2.有效的算法需在多项式时间内运行完成,即∃P;
3.当可彻底避免过拟合时,通过最小化经验误差就可获得最优解,即P=NP;
4.但实际上P≠NP;
5.过拟合无法避免。
二、评估方法
理想:通过评估学习器的泛化误差,选出泛化误差最小的学习器。
实际:泛化误差只能通过测试求得的测试误差来表现。
【测试误差】:学习器在测试集上的实际预测输出与测试样本的真实输出之间的差异。
【数据集】:一组记录的集合。D={x1,x2,x3...xm}
为了实现测试、表现出学习器的泛化误差从而进行评估,需要在数据集D中产生出训练集S与测试集T,其中测试集应尽可能与训练集互斥。
通过对数据集不同的处理方法,可以分出不同的训练集与测试集,常见的做法有如下三种。
1.留出法
【留出法】:直接将数据集D划分为两个互斥的集合,其中一个集合作为训练集S,另一个作为测试集T,即D=S∪T,S∩T=∅。
如上图,不是西瓜,是两个同心圆。其中内圆红色部分为训练集,外环绿色部分为测试集,两部分是两个互斥的集合。
除此之外,留出法还要尽可能的保持数据分布的一致性,要保持样本类别比例相似,从采样的角度看待数据采集的划分过程,保留类别比例的采样方式通常称为“分层采样”。就好比它真是一个西瓜,按甜度将其分为七块,采样时每一块都要按照相同的所占比例去采。这七类数据集的测试集与训练集的比值应是相等的。
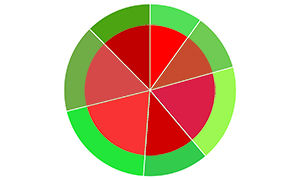
单次使用留出法得到的结果往往不稳定可靠,一般采用若干次随机划分,重复进行实验评估后取平均值作为留出法的评估结果。
例如测试集分别取此图中三组同心圆中绿色的部分,得出的结果再取平均值,就是留出法的评估结果。
总结:
留出法的特点:1.直接划分训练集与测试集、2.训练集和测试集均分层采样、3.随机划分若干次,重复试验取均值
p.s.上面五幅图,用圆心角来体现数据分布的一致性,无论是训练集还是测试集,均在360度范围内分布。
2.交叉验证法
【交叉验证法】:先将数据集D分为k个大小相似的互斥子集,即D=D1∪D2∪...∪Dk;Di∩Dj=∅(i≠j),如下图。
每个子集Di都尽可能保持数据分布的一致性,即每个子集仍然要进行分层采样。每次用k-1个子集作为训练集,余下的那个子集做测试集。这样可以获得k组“训练/测试集”,最终返回的是k个结果的均值。
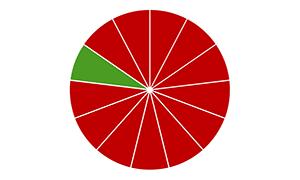
如上图,每个绿色的部分都为测试集,其余红色部分为训练集。
与留出法相似,交叉验证法也需要进行多次试验,用不同的划分方法重复p次(但每次还是划分为k组),再取均值。
总结:
交叉验证法得到的结果是均值的均值,即p个“k个结果的均值”的均值,因此交叉验证法又可以叫做p次k折交叉验证。
交叉验证法的特点:1.每个子集都会做测试集、2、每个子集分层采样、3.单次k折,切换测试集试验取均值、4.k折划分p次,重复试验再取均值
优点:准确;缺点:开销大
p.s.上面两幅图,用点到圆心的距离来体现数据分布的一致性,任何子集均有与圆心距离在0到半径长度范围内的点。
3.自助法
【自助法】:对有m个样本的数据集D,按如下方式采样产生数据集D':每次随机取一个样本拷贝进D',取m次(有放回取m次)。
按此方法,保证了D'和D的规模一致。但D'虽然也有m个样本,可其中中会出现重复的样本,而D中会存在D'采样没有采到的样本,这些样本就留作测试集。
某样本在m次采样中均不会被采到的概率是: ,取极限可得
由此可知,理论上有36.8%的样本没有出现在在D'之中。
优点:训练集与数据集规模一致;数据集小、难以有效划分训练集和测试集时效果显著;能产生多个不同的训练集;
缺点:改变了训练集的样本分布,引入估计偏差。
理想:通过评估学习器的泛化误差,选出泛化误差最小的学习器。
那么,上一节通过留出法、交叉验证法和自助法得到了可以表现泛化误差的测试误差后,如何选出表现最佳的学习器呢?这就需要对泛化能力有一个评价标准。简单举个例子就是:得到了值,带入标准之中,选出最终结果。
【性能度量】:衡量泛化能力的评价标准。
但实际上的性能度量,还要反映任务需求。在对比不同学习器的能力时,使用不同的性能度量往往会导致不同的评判结果。什么样的学习器是好的,不仅取决于算法和数据,还决定于任务需求。
预测任务中,评估学习器f的性能,需要将学习器的预测结果f(x)同真实标记y进行比较。
所以现在主要讨论的是监督学习。
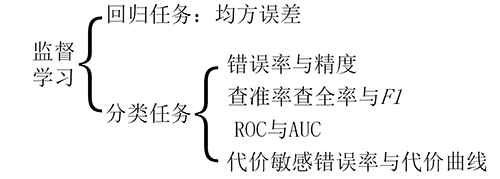
如图是监督学习的性能度量,其中回归任务的性能度量一般采用均方误差,而分类任务的性能度量多种多样。
1、回归任务的性能度量——均方误差:
公式如下:
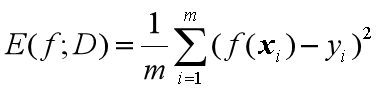
可知,均方误差是m个离散样本的方差的平均数。
但对于数据分布Ɗ和概率密度p(·),均方误差的计算公式如下:
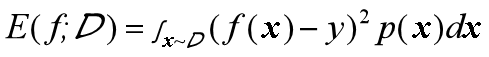
可知,此时样本可以看做非离散样本而是连续样本。
性能度量方法:通常,均方误差大的模型性能差,均方误差小的模型性能好。
均方误差反应的是回归任务模型判断正确与否的能力。
2、分类任务的性能度量1——错误率与精度
错误率:分类错误的样本占样本总数的比例。
精度:分类正确的样本占样本总数的比例。
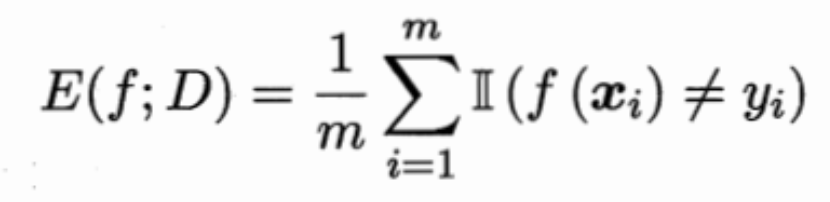
错误率是m个离散样本的指数函数和的平均数。
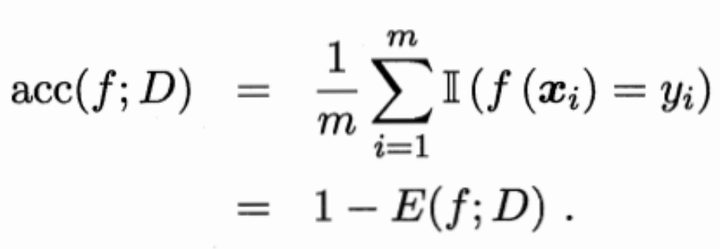
精度与错误率相同,也是m个离散样本的指数函数和的平均数,但两者的指数函数不同。
但对于数据分布Ɗ和概率密度p(·),错误率和精度的计算公式如下:
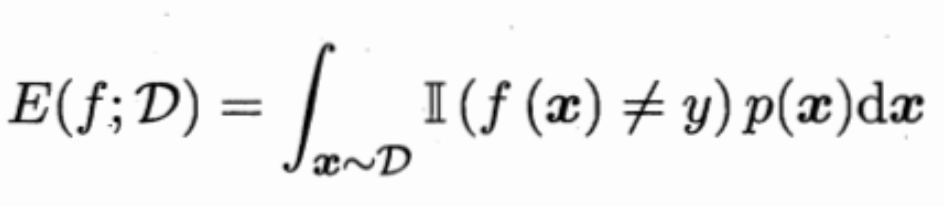
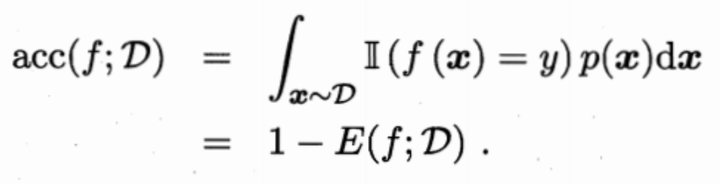
可知,此时样本可以看做非离散样本而是连续样本。
性能度量方法:通常,错误率低精度高的模型性能好,错误率高精度低的模型性能差。
错误率与精度反应的是分类任务模型判断正确与否的能力。
3、分类任务的性能度量2——查准率、查全率与F1
当需要反应的不是判断正确与否的能力,而是正例、反例查出的准确率时,就不能用错误率和精度作为判断分类任务模型的性能度量了。
判断得是否正确,在二分类任务中有四种表现形式,还拿西瓜🍉举例:
好西瓜判断成好西瓜,判断正确①;好西瓜判断成坏西瓜,判断错误②;
坏西瓜判断成好西瓜,判断错误③;坏西瓜判断成坏西瓜,判断正确④;
其中,①和④都是判断正确,②和③都是判断错误。错误率和精度是①和④、②和③的综合判断,只有判断正确与否的概念,没有正例反例的区别。
所以要引入查准率(P)、查全率(R)的概念。
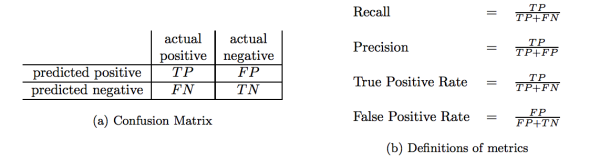
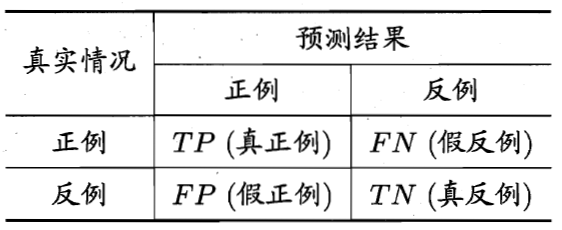
下表是二分类结果混淆矩阵,将判断结果分为四个类别,真正例(TP)、假正例(FP)、假反例(FN)、真反例(TN)。

查准率:【真正例样本数】与【预测结果是正例的样本数】的比值。
查全率:【真正例样本数】与【真实情况是正例的样本数】的比值。
查准率是在讲,挑出的好瓜里头,有多少真的是好瓜。所以当希望选出的好瓜比例尽可能高的时候,查准率就要高。(当瓜农面对零售时,会逐个判断哪一个是好瓜,然后对每一个顾客说:“保校保甜,不甜不要钱。”如果瓜农的查准率不高,他要赔死了。)
查全率是在讲,挑出来真的好瓜,占总共好瓜个数的多少。所以当希望尽可能多的把好瓜选出来的时候,查全率就要高。(当瓜农面对批发时,就不要求每个都甜了,尽可能多的把好瓜都挑出来就行了,不然就浪费了好瓜。)
一般来说,查准率高时,查全率偏低;查全率高时,查准率偏低。通常只在一些简单任务中,查准率和查全率都偏高。
性能度量的方法:1、直接观察数值;2、建立P-R图。
直接观察数值已经介绍过了,现在介绍P-R图。
P-R图,即以查全率做横轴,查准率做纵轴的平面示意图,通过P-R曲线,来综合判断模型的性能。
但值得一提的是,同一个模型,在同一个正例判断标准下,得到的查准率和查全率只有一个,也就是说,在图中,只有一个点,而不是一条曲线。
那么要得到一条曲线,就需要不同的正例判断标准。
在判断西瓜好坏的时候,我们不是单纯的将西瓜分成好坏两堆,左边一堆好瓜,右边一堆坏瓜。

而是对预测结果进行排序,排在前面的是学习器认为最可能是正例的样本,排在最后面的是最不可能的样本。

现在按顺序,依次将每一个样本划分为正例进行预测,就得到了多组查准率和查全率的值了。
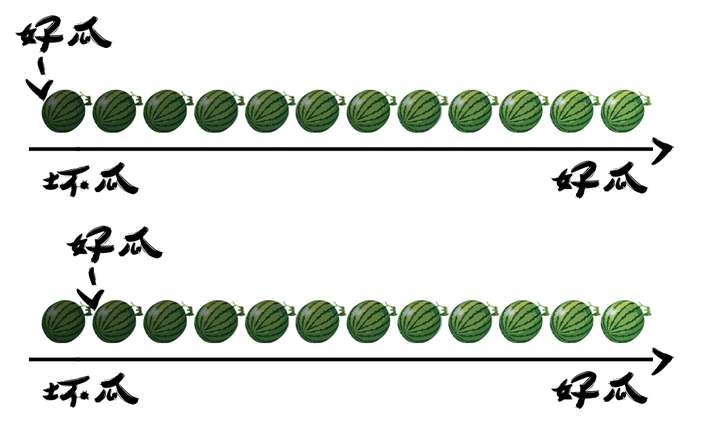
多组值就是多个点,样本充足的时候,可以连成一条平滑的曲线,即为P-R曲线。
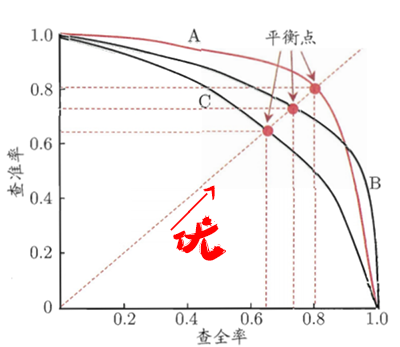
得到P-R图后,如何判断哪个学习器性能更佳?
当曲线没有交叉的时候:外侧曲线的学习器性能优于内侧;
当曲线有交叉的时候:
第一种方法是比较曲线下面积,但值不太容易估算;
第二种方法是比较两条曲线的平衡点,平衡点是“查准率=查全率”时的取值,在图中表示为曲线和对角线的交点。平衡点在外侧的曲线的学习器性能优于内侧。
第三种方法是F1度量和Fβ度量。F1是基于查准率与查全率的调和平均定义的,Fβ则是加权调和平均。
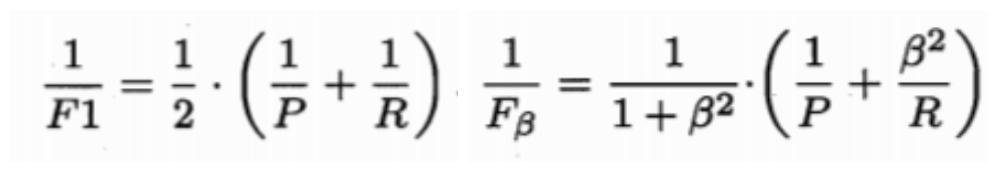

通过比较两条曲线的F1,来判断哪个学习器性能更好。
但在不同的应用中,对查准率和查全率的重视程度不同,需要根据其重要性,进行加权处理,故而有了Fβ度量。β是查全率对查准率的相对重要性。
β>1时:查全率有更大影响;β=1时:影响相同,退化成F1度量;β<1时:查准率有更大影响。
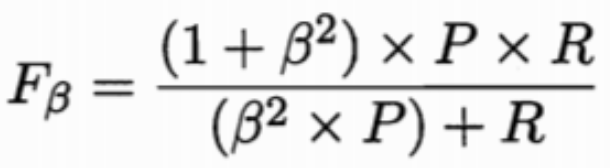
以上是一个二分类混淆矩阵的查准率和查全率判断。
但实际情况中,一个分类学习器往往并不只有一个二分类混淆矩阵,当多次训练/测试或是在多个数据集上进行训练/测试的时候,就会出现多个二分类混淆矩阵。当需要综合考虑估计算法的“全局性能”时,有两种解决办法。
宏:在n个混淆矩阵中分别计算出查准率查全率,再计算均值,就得到“宏查准率”、“宏查全率”和“宏F1”。
微:先将n个混淆矩阵的对应元素进行平均,再计算查准率查全率和F1,就得到“微查准率”、“微查全率”和“微F1”。
4、分类任务的性能度量3——ROC与AUC
与P-R图相同,ROC图通过对测试样本设置不同的阈值并与预测值比较,划分出正例和反例。再计算出真正例率和假正例率。P-R图逐个将样本作为正例,ROC图逐次与阈值进行比较后划分正例。本质上,都是将测试样本进行排序。

真正例率(TPR):【真正例样本数】与【真实情况是正例的样本数】的比值。(查全率)
假正例率(FPR):【假正例样本数】与【真实情况是反例的样本数】的比值。
ROC图全名“受试者工作特征”,以真正例率为纵轴,以假正例率为横轴。
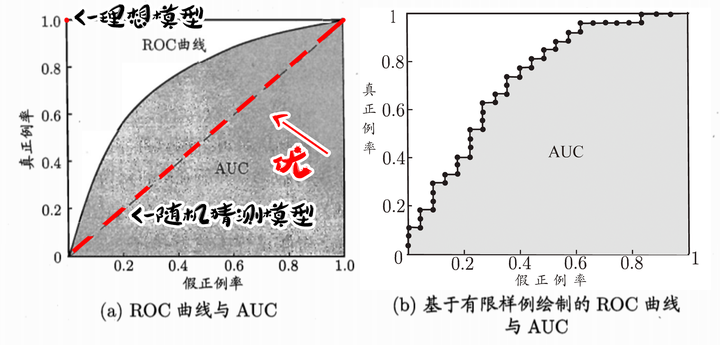
如图,理想模型是真正例率为100%,假正例率为0%的一点。随机猜测模型则是真正例率与假正例率持平的直线。由此可知,在随机猜测模型左上方的曲线和在其右下方的曲线都代表了什么。(右下方的模型,还不如随机猜测准。)
性能度量的方法:绘制ROC曲线
当曲线没有交叉的时候:外侧曲线的学习器性能优于内侧;
当曲线有交叉的时候:比较ROC面积,即AUC。
5、分类任务的性能度量4——代价敏感错误率与代价曲线
还是之前的西瓜🍉例子:
好西瓜判断成好西瓜,判断正确①;好西瓜判断成坏西瓜,判断错误②;
坏西瓜判断成好西瓜,判断错误③;坏西瓜判断成坏西瓜,判断正确④;
②和③都是判断错误,错误率是②和③的综合。虽然从错误率的角度看,把好瓜判断成坏瓜和把坏瓜判断成好瓜,都是判断错了。但实际上,这两种错误的判断所付出的代价却是不同的。把好瓜判断成坏瓜,会浪费一个好瓜;而把坏瓜判断成好瓜,则可能吃坏一个顾客的身子。
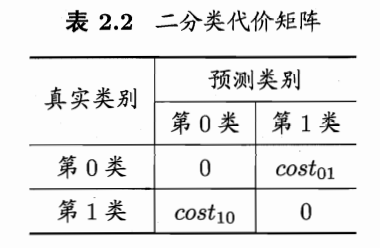
换句话说,前面介绍的性能度量,大都隐式地假设了“均等代价”,而为权衡不同类型错误所造成的不同损失,应为错误赋予:“非均等代价”。
下图为二分类代价矩阵,其中 表示将第i类样本预测为第j类样本的代价。
而如下公式就是被赋予了非均等代价的错误率:
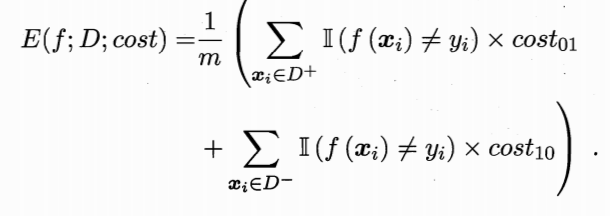
在这样的非均等代价下,ROC曲线不能直接反映出学习器的期望总体代价,而“代价曲线”则可以达到目的。
性能度量的方法:绘制代价曲线
代价曲线的横轴是正例概率代价P(+)cost,纵轴是归一化代价 。
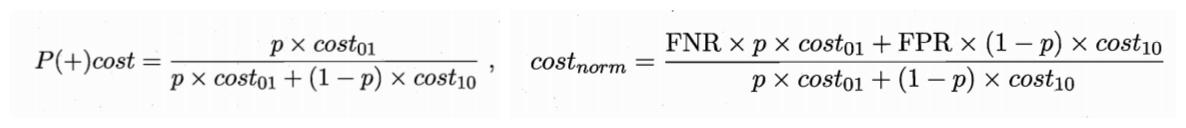
其中,p是样例为正例的概率;FNR是假反例率;FPR是假正例率。
真正例率(TPR):【真正例样本数】与【真实情况是正例的样本数】的比值。(查全率)
假正例率(FPR):【假正例样本数】与【真实情况是反例的样本数】的比值。
假反例率(FNR):【假反例样本数】与【真实情况是正例的样本数】的比值。(1-查全率)
(P.S.这里容易绕混,真正,正正为正;假反,负负得正;假正,负正得负;真假,正负为负)
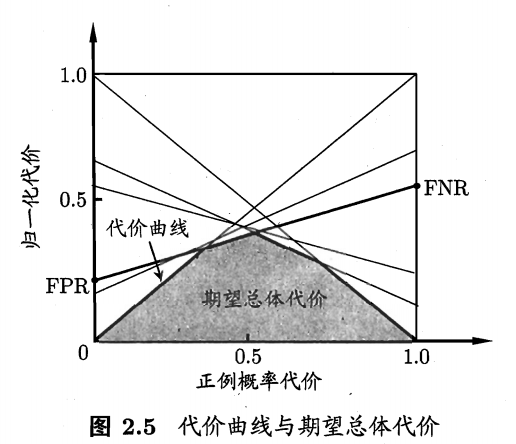
绘制方法:
ROC曲线上取一个点(FPR,TPR);
取相应的(0,FPR)和(1,FNR),连成线段;
取遍ROC曲线上所有点并重复前步骤;
所有线段的下界就是学习器期望总体代价。
实际上就是通过将样例为正例的概率p设为0和1,来作出曲线的所有切线,最后连成曲线。
四、比较检验
0.回顾
有了评估方法和性能度量,就可以对学习器性能进行比较了。
由于这些名字实在晦涩拗口,我们再来回顾一下评估方法和性能度量都是什么。
评估方法:从数据集D中分出训练集S和测试集T。
常见的评估方法:留出法、交叉验证法、自助法。
性能度量:对学习器的泛化性能进行评估时衡量模型泛化能力的评价标准。
常见监督学习的性能度量:
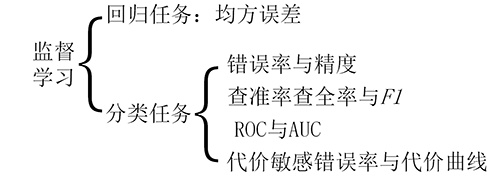
综上,评估方法将数据集分类,其中一部分用于训练,另一部分用于测试。而性能度量是一系列数值和图像,在训练完毕后,通过比较这些数值和图像来反映学习器性能的优劣。
那么问题来了,怎么比较?
实际上,这个比较很复杂,涉及三个重要因素。
1、希望比较的和实际获得的性能并不相同,两者对比结果也可能不会相同。

2、测试集的性能与测试集本身的选择有很大关系,也就是说,可能数据好,性能就好,数据不好,性能也跟着不好。

3、很多机器学习算法都具有随机性,相同的参数、相同的测试机,运行多次,结果却不同。
了解了这三个重要因素,才能对如何评估学习器性能优劣有一些思路。
1、假设检验
比较检验的重要方法是统计假设检验,它为我们进行学习器性能比较提供了重要依据。
但是由于书中没有对假设检验做一些什么详细的介绍,而是默认大家都了解了这部分的知识,所以很多人可能看到这就有些吃力了。
所以想学好计算机,数学还是很重要的。
不了解假设检验的原理,这部分内容等于是看不下去的。
所以先来了解一下假设检验。
假设检验(Hypothesis Testing)是数理统计学中根据一定假设条件由样本推断总体的一种方法。
浙大第四版书中的假设检验定义如下:
在总体的分布函数完全未知或已知其形式,但不知其参数的情况,为了推断总体的某些未知特性,提出某些关于总体的假设。我们要根据样本对所提出的假设作出是接受还是拒绝的决策。
介于数学定义总是云里雾里复杂难懂,笔者在此梳理一下。
假设检验四步走:
1、条件:满足情况。(总体的分布函数完全未知或已知其形式,但不知其参数)
2、目标:以推断总体的某些未知特性为目标。
3、方法:提出某些关于总体的假设。
4、行动:根据样本对所提出的假设作出是接受还是拒绝的决策。
那么假设检验在机器学习的【比较检验】中究竟如何应用呢?以让我们以分类任务的【错误率】为例子,从这四步里分析:
1、条件:
现实中我们不知道学习器的泛化错误率,只能获知其测试错误率。但是二者的分布情况极有可能相似。这就符合了定义中“分布函数完全未知或已知其形式但不知其参数”的情况。
也就是说:泛化错误率的分布未知,但可通过测试错误率去推断。
2、目标:
情况符合了,可总体有什么未知特性要我们来推断?
“若在测试集上观察到学习器A比B好,则A的泛化性能是否在统计意义上优于B,以及这个结论的把握有多大。”这便是总体的未知特性。
未知特性也有了,现在要进行假设了。
3、方法:
以书中的例子为例,“ ”,将泛化错误率假设为某数值
。
4、行动:
通过显著度来判断做出的假设该被接受还是该被拒绝。
梳理清楚了思路,让我们彻底回到书中的例子中来。
先说进行一次估计的例子:
首先标注一下各个符号:
测试错误率:
泛化错误率:
测试样本数:
误分类样本数:
其中,泛化错误率 是一个完全未知的只能推测的数值,测试错误率
则是可以获知的未知数值。测试样本数
是给定的,误分类样本数
是测试得知的。
在测试得知了 之后,可推断出,
(
和
成正比,比例系数为
),从而
可知。未知数就只剩下
。
在包含了 个样本的测试集上,【泛化错误率为
的学习器】被测得测试错误率为
的概率为:

这个概率数值 ![P(\tilde{\epsilon};\epsilon)]() 有什么用呢?
有什么用呢?
我们在解释完之后回答。
这个概率,表达了【泛化错误率为 的学习器】被测得【测试错误率】为
的可能性。
取0~100%。若以这个【可以测得的测试错误率
】作为自变量,以概率
为因变量,建立平面坐标图,则对于不同的测试错误率,有不同的可能性。在某点可能性越高,这个未知的【泛化错误率
】和这个点代表的测试错误率的关系就越密切。
现在要找其可能性最高的点,就要对概率 求
的导数,导数为0时,存在极值。
而对此概率函数求导并解出导函数等于0的式子之后,发现存在一个值 ,使得
在
时最大,
增大时减小。整个图像其实是个山峰形状,符合二项分布。
那么此时也可以反过来讲,如果这个泛化错误率 已知为
,则理论上,横坐标为
的概率值
是最大的。这也和书中图2.6的例子一致。
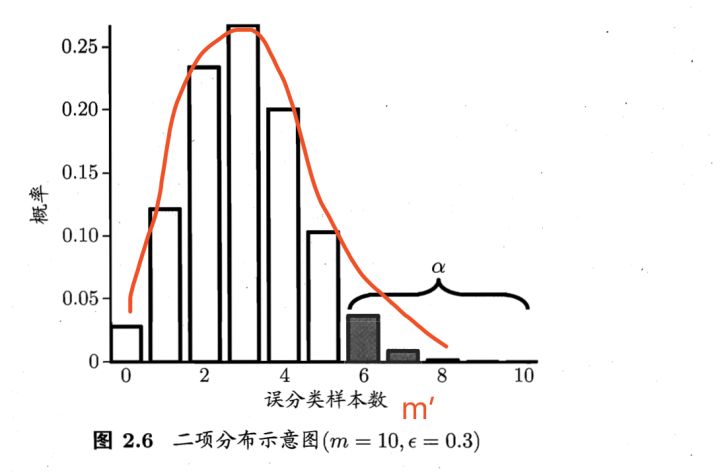
即:若泛化错误率为 ,则测试错误率也为
的概率最大(可能性最高)。
那么我现在可以回答上面那个问题了。
这个概率数值的用处,就是让我们得到了一个可能是最大的泛化错误率数值 ![\epsilon_{0}]() ,使得我们可以用这个数值来进行假设,假设这个学习器的泛化错误率不会超过
,使得我们可以用这个数值来进行假设,假设这个学习器的泛化错误率不会超过 ![\epsilon_{0}]() .
.
即假设:“ ”。
没有这个概率 ,我们连假设什么都不知道,只能瞎鸡儿假设(摊手)。
那么有了假设,就可以进行检验了。
到底要不要接受这个假设呢?
我们来检验一下。
这里就涉及假设检验的另外一大难点,也是最令我头疼的一点,显著度 (也叫显著性水平)。
显著性水平是估计总体参数落在某一区间内,可能犯错误的概率,用α表示。显著性是对差异的程度而言的,程度不同说明引起变动的原因也有不同:一类是条件差异,一类是随机差异。它是在进行假设检验时事先确定一个可允许的作为判断界限的小概率标准。
这个显著度 ,是事先确定好的一个非常小的值,比如0.05啦,0.1啦什么的。(上图是为了看清楚而随便画的)
有了这个显著度 ,我们就确定了一个发生【判断错误】的概率上限。(什么叫【判断错误】呢?就是当
为真时拒绝接受
,所以“
”也被称为置信度。)
确定了这个上限之后,就可以很方便的得出一个检验假设的门槛值 (此门槛值为泛化错误率的最大值),若测试错误率
小于这个门槛值
,则可以说,在
的显著度下(或在
的置信度下),接受这个“
”的假设。反之,若测试错误率大于这个门槛值(测试错误率比最大的泛化错误率还大),则说明,在
的显著度下,应该拒绝这一假设。
一次估计的说完了,再简单说说多次的。
现实中我们并非仅作出一次留出法估计,而是做多次,所以会得到不同的多个测试错误率:
假设测试了 次,就会得到相应的均值
和方差
。
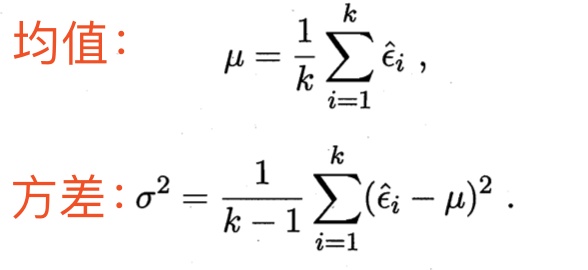
考虑到这 个测试错误率可以看做泛化错误率
的独立采样,则根据公式
,
为自由度为
的
分布,变量
服从自由度为
的
分布。(
服从正态分布,
服从自由度为
的
分布)
由此图和 分布图的性质可知,最高点处就是测试错误率的最大值
。
现在要重新假设了,“ ”。
接下来就是继续确定显著度 ,确定门槛值(此处用双边假设),最后进行在置信度为
下的判断了。

第二章写了这么久,还是没写完,实在是因为这一章是机器学习问题的一个核心——即如何对学习器进行评估,方法和依据都什么。私以为这部分,是机器学习的重中之重。
下次发布的没有意外的话会是第二章的最会一个分章,笔者将介绍完比较检验的其他几种方法以及偏差与方差的关系,并尝试解答课后习题。
2、交叉验证 ![t]() 检验
检验
学习最重要的部分就是复习。
先回顾一下 折交叉验证。
交叉验证法:先将数据集划分为
个大小相思的互斥子集,即
,每个子集都尽可能的保持数据分布的一致性,即从D中通过分层采样得到。
回顾完了,开始介绍比较检验的第二种检验方法:交叉验证 检验。
还是用错误率的比较进行举例。
即:评估方法:交叉验证法。性能度量:错误率。比较检验:交叉验证 检验。
现在有两个学习器A和B,使用 折交叉验证法得到测试错误率分别为
和
。其中
和
是在相同的第
折训练/测试集上得到的结果。
注意,此时的测试错误率和之前的假设检验那一节的测试错误率采用了不同的符号,此时由于没有提到泛化错误率,测试错误率被标记为 ,只不过增加了上下角标,请各位不要将其与上一节的泛化错误率混淆。
这种情况,可用 折交叉验证“成对
检验”来进行比较检验。
如果说前一种的假设检验是得到单个学习器的泛化错误率的大致范围假设,那么这一种检验方法就是在比较A、B两学习器性能的优劣了(不过偏向于验证A、B性能是否相同)。
但是啊,交叉验证 检验,本质上,还是一种假设检验。
基本思想:若两个学习器的性能相同,则它们使用的训练/测试集得到的测试错误率应相同,即 。
实际上却不会像理想状态一样,两个学习器的测试错误率并不完全相同,而是存在一定的微小差值。我们想要判断两个学习器的性能是否有显著差别,就要利用这个差值进行假设检验。
若两个学习器性能相同,这个差值均值应该为0。因此可对这k个差值对“学习器A和B性能相同”这个假设做 检验。
1、先对每一对结果求差,
2、计算出这k个差值的均值 和方差
3、根据 检验的公式
,得
,满足自由度为
的
分布,故在显著度
,若其小于临界值
,则假设不能被拒绝,即认为两个学习器性能没有显著的差别。反之则认为平均错误率小的性能更优。
这里 是分布上尾部累积分布为
的临界值。
但是这样使用 折交叉验证法,通常情况下会因为样本有限,使得不同轮次的训练集产生一定程度的重叠。这样训练出来的学习器,会让得出的这组测试错误率无法做到彼此完全独立。
而进行有效的假设检验的一个重要的前提就是:测试错误率均为泛化错误率的独立采样。(例如 分布就需要随机变量X和Y相互独立。)
所以为了缓解这个问题,可采用“5×2交叉验证”法。
5×2交叉验证法
所谓“5×2交叉验证”法,就是做5次2折交叉验证,而在每次2折交叉验证之前随机将数据打乱,使得5次交叉验证中的数据划分不重复。
对两个学习器A和B,第 次2折交叉验证将产生两对测试错误率:
、
和
、
,对它们分别求差,得到第1折上的差值
和第2折上的差值
。
为了缓解测试错误率的非独立性,仅对第一次2折求均值 ,然后对每次实验结果都求方差。
(这里笔者觉得书中公式有问题,这里的方差应该是样本方差,故应该是每个样本值与全体样本值平均数之差的平方和的平均数,即 ,书中未求平均数,故笔者认为方差:
)。
但经过思考,笔者认为书中公式没有问题, 是差值的均值
而不是期望
除非正好
,否则我们一定有
,而不等式右边的才是的对方差的“正确”估计,换言之方差被估计小了,为了让方差的估计是无偏的,应将n-1,即2-1=1。也就不用除以什么了。
也就说正确的公式为:
由此均值方差,可以得到一个 分布。
3、McNemar检验
McNemar检验适用于二分类问题,用于某些 2 × 2 表格的配对样本。通过联列,可以获得学习器A和B的分类结果的差别。下表即为两分类器分类差别列联表, 为样本数。
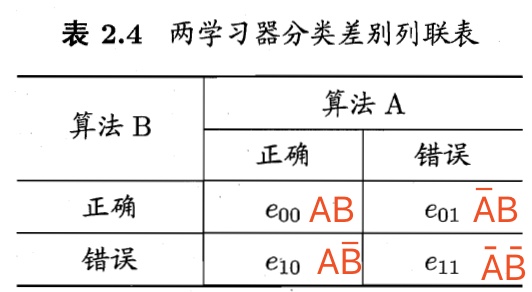
是A、B都被分类为正确的样本数;
是A被分类为错误,B被分类为正确的样本数;
是A被分类为正确,B被分类为错误的样本数;
是A、B都被分类为错误的样本数。
现在若假设,两学习器性能相同,则理想状态应有 。
但是实际操作中 和
在不同的测试集上会有一些差别。
但是| |为什么符合正态分布,,,按理说,实际生活中,凡自然状态下的整体数据分布几乎都符合正态分布,那么当假设两学习器性能相同的时候,如果用大量不同的测试集进行测试,这个差值应该就可能符合正态分布。故
符合
分布。
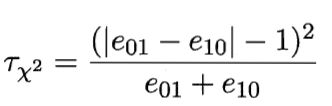
但上式中的“-1”并非因为 的均值
为1,实际上均值
应近似为0,这里的“-1”,是为了连续性矫正。有关连续性矫正的问题,维基百科给出了比较简单的解释,我也就不重复了。
4、Friedman检验与Nemenyi后续检验
当有多个算法需要进行比较的时候,有两种思路。
一种做法是在每个数据集上分别列出两两比较的结果,交叉验证 检验、McNemar检验都属于这种;另一种则更为直接,即为使用基于算法排序的Friedman检验。
Friedman 检验的问题是k个样本的位置参数(用 ,
,
,…,
表示)是否相等,在机器学习领域被用来判断各种算法的性能是否都相同。
假设检验问题:
:
,即k个样本无显著差异。
:不是所有的位置参数都相等(不是所有的算法性能都相同),即k个样本有显著差异。
提出待检验的假设后,获得的数据排出一个k行n列的表, 列代表不同的受试者或匹配的受试小组(各个算法), 行代表各种条件或处理(数据集)。
由于区组的影响,Friedman检验首先在每一个区组中计算各个处理的秩,再把每一个处理在各区组中的秩相加。

其中 表示在第
个区组中
处理的秩, 行和为
如果为 真,则每一列中秩的分布应该是随机的, 即各个秩出现在所有列中的频数应几乎相等。
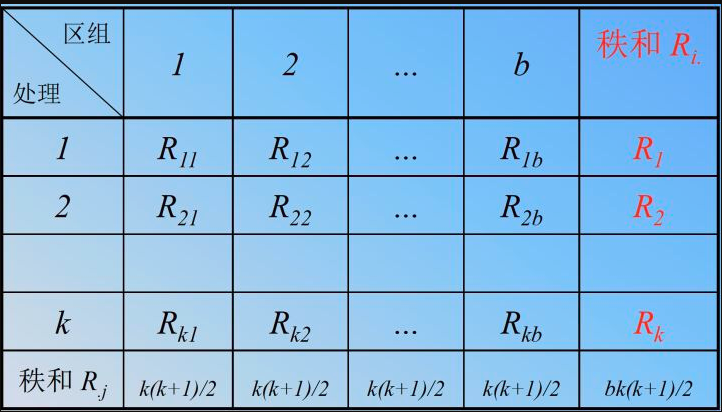
在零假设成立的情况下,各处理的平均秩 有下述性质:
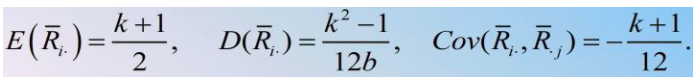
接下来计算处理平方和( )。
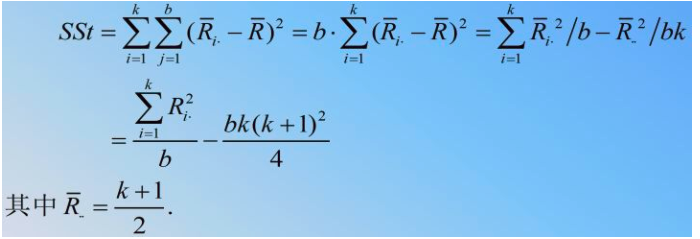
Friedman检验统计量为 :
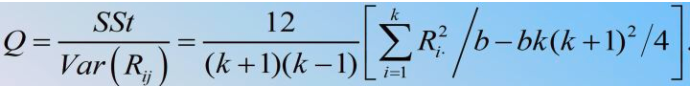
Friedman建议用 乘
得校正式
:

当假设“所有算法的性能相同”被拒绝的时候,需采用后续检验来进一步区分各算法,常用的是Nemenyi后续检验,该算法计算出平均序值差别的临界值域 ,若两个算法的平均序值之差超过临界值域,则应以相应的置信度拒绝“两个算法性能相同”这一假设。
五、偏差与方差
介绍了估计泛化性能的评估方法、性能度量和检验方法后,还需要知道泛化性能究竟由什么组成。
“偏差-方差分解 ”是解释学习算法泛化性能的重要工具。
解释这个概念前,先明确一下各变量名:
测试样本:x
测试样本x在数据集中的标记:
测试样本x的真实标记:
训练集:
从训练集 上学得的模型
模型 在测试样本x上的预测输出
(x;
)
除了书中介绍的这些之外,还有一个概念,也不知是由于书中印刷错误还是因为过于省略,导致公式整个存在理解错误:
数据分布:Ɗ
知道了这些变量后,下面介绍几个概念:
1、 (x)(预测输出的期望):学习算法的期望预测。
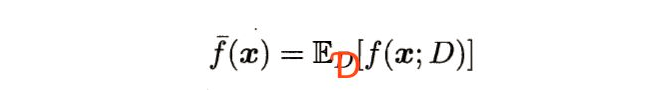
【所有可能的训练数据集】(数据分布Ɗ)训练出的【所有模型预测输出】的期望值。
2、 (方差):使用样本数相同的不同训练集产生的方差。

【在分布Ɗ上】的【不同训练集训练出的模型】的【预测输出】与【预测输出期望值】的比较。
3、 (偏差):期望输出与真实标记的差别。

用【所有可能的训练数据集】(数据分布Ɗ)训练出的【所有模型预测输出】的期望值与【真实模型的输出值】比较得出的差异。
4、 (噪声):数据集标记和真实标记的方差。
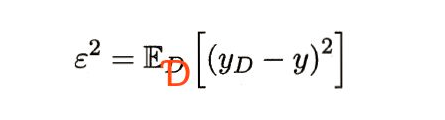
噪声数据主要来源是训练数据的误标签的情况以及输入数据某一维不准确的情况。
为了便与讨论,假定噪声期望为0,则对算法的期望泛化误差进行分解可得:
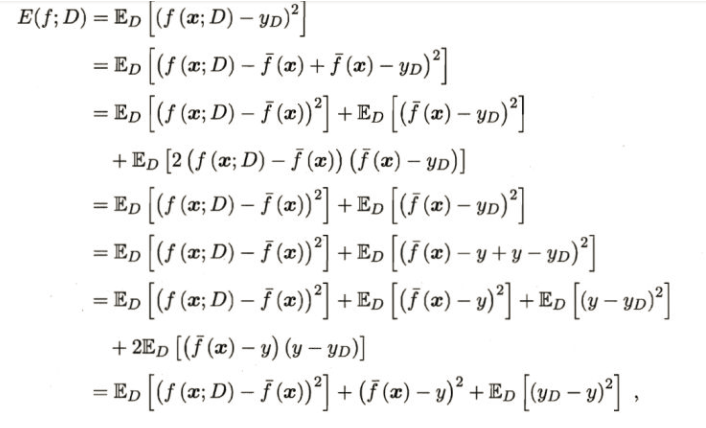
故,
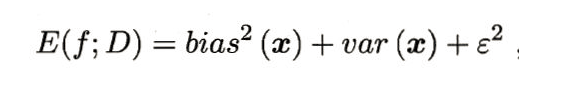
也就是说,泛化误差=偏差+方差+噪声。
回顾一下偏差、方差、噪声的含义:

偏差为“精”,方差为“确”。一般来说,偏差和方差是有冲突的,这称为“偏差-方差窘境”,如下图所示。

〖二、习题探讨〗
1.数据集包含1000个样本,其中500个正例,500个反例,将其划分为包含70%样本的训练集和30%样本的测试集用于留出法评估,试估算共有多少种划分方式。
解:这是一个简单的组合问题,考察的是留出法“分层采样”的性质。500正例500反例,按“37开”划分后,训练集有350正例350反例,测试集有150正例150反例,正例和反例的划分策略相互独立。则共有: 种划分方式。
2.数据集包含100个样本,其中正反例各一半,假定学习算法所产生的模型是将新样本预测为训练样本数较多的类别(训练样本数相同时进行随机猜测),试给出用10折交叉验证法和留一法分别对错误率进行评估所得的结果。
解:
留一法是交叉验证法的一种,其含义是:假设有N个样本,将每一个样本作为测试样本,其它N-1个样本作为训练样本。这样得到N个分类器,N个测试结果。用这N个结果的平均值来衡量模型的性能。
现在有100个样本,50正例50反例,则10折交叉验证法中,每一折正反比例相同,所以将结果判断为正反例的概率也是一样的,即进行随机猜测,则每次错误率的期望是50%。由于有100个样本,则测试应为10次10折交叉验证,最终返回的是这10次测试结果的均值,即50%。
而留一法中,若一次留下的一个测试样本为反例,则新样本将都被预测为正例;反之,若一次留下的一个测试样本为正例,则新样本将都被预测为反例。
前者,正例:反例=50:49,预测为正例,测试样本是反例,错误率100%;
后者,正例:反例=49:50,预测为反例,测试样本是正例,错误率100%。
由于进行的是100次留一法验证,取得也是这100次结果的均值,最终结果是100%。
3.若学习器A的F1值比学习器B高,试析A的BEP值是否也比B高。
先介绍相关定义:
查准率 P = TP / (TP + FP)
查全率 R = TP / (TP + FN)
BEP:平衡点,Break-Event Point,是“查准率 = 查全率”时P-R曲线上的的取值。
度量:
= 2 * P * R / (P + R) = 2 * TP / (样例总数 + TP - TN) 是基于查准率和查全率的调和平均。
探讨:
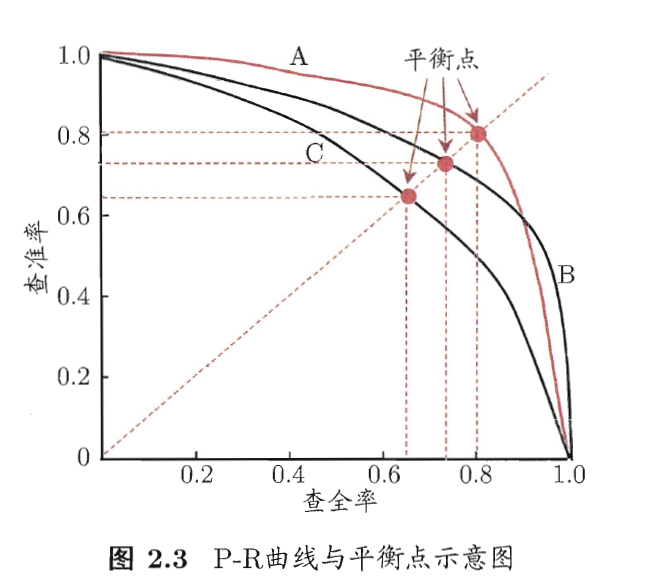
由图可知,BEP只是P-R曲线上的一个查准率和查全率相等时的平衡点,是曲线上的一点。而 则是基于查全率和查准率的调和平均,理论上这一条曲线上有n个
值。
但是P-R图的来源是逐个把样本按照“最可能是正例”的顺序排序后,逐一把样本作为正例后求出其查准率和查全率绘制的。但实际上在解决具体问题时,会设置正例和反例的分界线,也就是说只能在曲线上取一个值。
那么这个值是不是BEP?
是某些学习器对查准率和查全率的重视程度不同而得到的加权调和平均。故
应该是对查准率和查全率重视程度相同的。但是重视程度相同是否等同于查准率=查全率?
答案应该是否定的。
理论上,如果存在两个BEP值相同的学习器,他们的F1却值不一样,那么这道题的结论就是否定的。
那么只要有两条曲线在BEP值点相交,却不在BEP值点取划分界限,就可以得到两个BEP值相同, 值却不同的点了。
不过 值既然是对BEP的补充和细化,其相对距离不会很远,即应在BEP附近某处取值。

所以,若学习器A的F1值比学习器B高,A的BEP值未必比B高。
4.试述真正例率(TPR)、假正例率(FPR)与查准率(P)、查全率(R)之间的联系。
查准率: 【真正例样本数】与【预测结果是正例的样本数】的比值。
查全率: 【真正例样本数】与【真实情况是正例的样本数】的比值。
真正例率: 【真正例样本数】与【真实情况是正例的样本数】的比值。
假正例率: 【假正例样本数】与【真实情况是反例的样本数】的比值。
依照公式可知,真正例率和查全率相等。
5.试证明(2.22)AUC=1−lrank
排序损失的计算公式(2.21)计算的是:对所有正例,得分比其高的反例数之和,并用m+m−进行归一化。
对于得分和该正例相同的反例,数量需要除以2。
ROC曲线中,每遇到一个正例向上走一步,每遇到一个反例向右走一步。对于所有的正例,其横坐标所代表的步数就是得分比其高的反例数。我们修改ROC空间的坐标,对横坐标乘以m−,对纵坐标乘以m+,在这个空间中每一步的刻度为1。
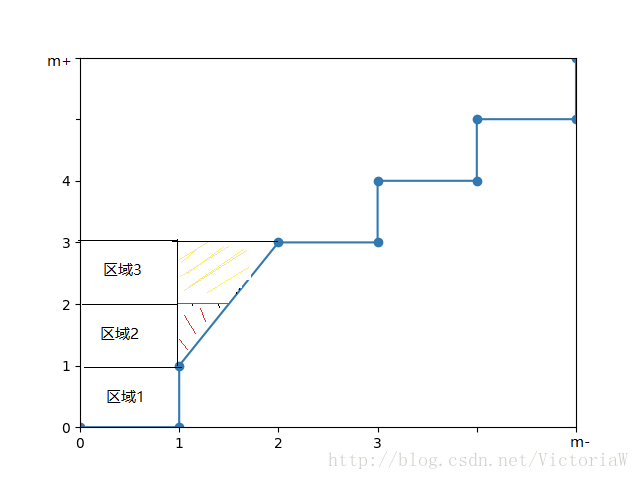
比如,上图中蓝色的线表示ROC曲线。根据这个曲线,我们可以知道正反例顺序:(反,正,[正,正,反],反,正,…)。其中,[]括起来的实例分数相同。对第一个正例,对应的区域1,区域1的面积表示排在其前面的反例数。
第二个正例和第三个正例是特殊情况,它们和一个反例得分是相同的。我们把这种情况一般化,假设有p个正例和q个反例的得分相同,那么有斜线对应的三角形的面积为q2∗p,这和公式(2.21)中的相应的情况吻合。
所以有:,,左右两边同时除以m+m−,得到公式(2.22)。
6.试述错误率与ROC曲线之间的关系
错误率:
ROC图像的横纵坐标分别是真正例率和假正例率:
真正例率:
假正例率:
ROC图像上的每个点,对应一个错误率。
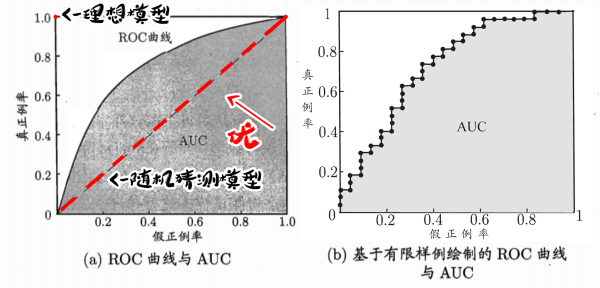
由于样本中,正反例比例确定,理想模型在(0,1)点上,故距离该点越近的点,错误率越低。
7.试证明任意一条ROC曲线都有一条代价曲线与之对应,反之亦然。
代价曲线绘制方法:
ROC曲线上取一个点(FPR,TPR);
取相应的(0,FPR)和(1,FNR),连成线段;
取遍ROC曲线上所有点并重复前步骤;
所有线段的下界就是学习器期望总体代价。
实际上就是通过将样例为正例的概率p设为0和1,来作出曲线的所有切线,最后连成曲线。

根据画图的步骤,就可知任意一条ROC曲线都有一条代价曲线与之对应,由于其数值一一对应,故反之亦然。
8.Min-max规范化和z-score规范化是两种常用的规范化方法。令x和x′分别表示变量在规范化前后的取值,相应的,令xmin和xmax表示规范化前的最小值和最大值,x′min和x′max分别表示规范化后的最小值和最大值,x¯和σx分别表示规范化前的均值和标准差,则min-max规范化、z-score规范化分别如式(2.43)和(2.44)所示。试析二者的优缺点。
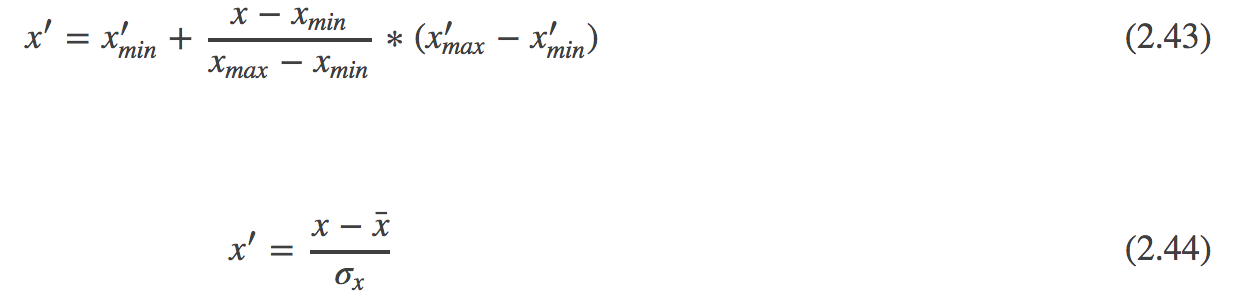
min-max对数据进行线性变换,保留了原始数据之间的关系;但是当点落在外时,无法进行规范化。
z-score对数据进行变换,使得均值为0,并且数据分布变得更紧密;但是对小的比较敏感。
9.试述卡方检验过程。
略。
10.试述在使用 检验中使用式(2.34)与(2.35)的区别。
探讨:
F分布主要用于方差分析、协方差分析和回归分析等,有两个自由度,本题中的两个自由度分别是(k-1)和(k-1)(N-1)。
如果说原始Friedman检验有哪里过于保守,恐怕就是没有考虑多个数据集对其造成的影响吧。



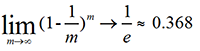

 浙公网安备 33010602011771号
浙公网安备 33010602011771号