神经网络中的损失函数

------------------------原文  https://blog.csdn.net/qq_34886403/article/details/83280726   ---------------------------

损失函数可以两大类：分类和回归。

回归损失：

1 L1loss L1损失

L1损失，也称为平均绝对误差MAE，简单地说就是计算输出值与真实值之间的绝对值大小。这种度量方法在不考虑方向的情况下衡量误差大小。和MSE的不同之处在于，MAE需要线性规划这种复杂的工具来计算梯度。同时 MAE对异常值更加稳健，因为他不需要平方。

2 SMOOTHLoss

L1Loss的平滑版，如果绝对值误差低于1则使用平方项的标准，否则L1项。它对异常值的敏感低于MSELoss

 

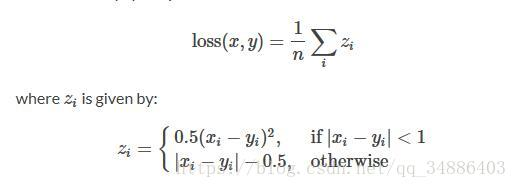
 3  MSELoss   L2损失

均方误差，预测值与实际观测值间的平方的均值。它值考虑误差的平均大小，不考虑其方向。但由于经过平方，与真实值偏离较多的预测值会受到更加严重的惩罚，同时MSE的数学特性很好，梯度更变的容易。

4 MBELoss

与L1损失很相似，唯一不同的是 没有绝对值，可以确定存在正偏差还是负偏差。

鲁棒性:

因为与最小平方相比，最小绝对值偏差方法的鲁棒性更好，因此，它在许多场合都有应用。最小绝对值偏差之所以是鲁棒的，是因为它能处理数据中的异常值。这或许在那些异常值可能被安全地和有效地忽略的研究中很有用。如果需要考虑任一或全部的异常值，那么最小绝对值偏差是更好的选择。
从直观上说，因为L2范数将误差平方化（如果误差大于1，则误差会放大很多），模型的误差会比L1范数来得大（ e vs e^2 ），因此模型会对这个样本更加敏感，这就需要调整模型来最小化误差。如果这个样本是一个异常值，模型就需要调整以适应单个的异常值，这会牺牲许多其它正常的样本，因为这些正常样本的误差比这单个的异常值的误差小。
稳定性：

最小绝对值偏差方法的不稳定性意味着，对于数据集的一个小的水平方向的波动，回归线跳跃很大。

分类损失：

1 CrossEntropyLoss

交叉熵误差，常用在分类问题。随着预测概率偏离实际标签，交叉熵会逐渐增加。他将nn.LogSoftmax()  和nn.NLLLoss组合在一个单独的类中。所示使用它并不需要在网络中加入softmax 。在多分类任务中，他非常有用。它具有可选参数权重。

2 NLLLoss

负对数似然损失函数。在前面LogSoftMax 就等价于CrossEntropyLoss，在多分类任务中很有用。