LeetCode: 51. N-Queens（Medium）

1. 原题链接

https://leetcode.com/problems/n-queens/description/

2. 题目要求

游戏规则：当两个皇后位于同一条线上时（同一列、同一行、同一45度斜线、同一135度斜线）时，便可以消灭其中一个皇后

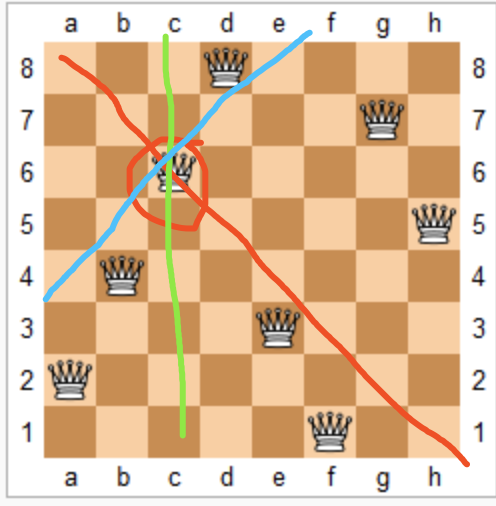
给出一个n*n的棋盘，要求棋盘上的n个皇后都不能被其他皇后吃掉，给出棋盘上n个皇后所有的摆放情况。

‘Q’代表此处放的是皇后，‘.’代表此处为空

4皇后的输出结果形式：

[[.Q.., ...Q, Q..., ..Q.],
[..Q., Q..., ...Q, .Q..]]

3. 解题思路

1. 将n*n的棋盘用一个长度为8的String类型数组表示，每一个元素代表棋盘中的一行，由长度为8的字符串表示，例如：

String[] queens = {".......Q", "...Q....", "Q.......", "..Q.....", ".....Q..", ".Q......", "......Q.", "....Q..."};

2. 采用回溯的思想进行迭代，该位置满足则设为Q，否则回溯到上一步，重新选择列的位置进行迭代

4. 代码实现

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

public class NQueens51 {
    public static void main(String[] args) {
        NQueens51 nq = new NQueens51();
        List<List<String>> res = nq.solveNQueens(8);
        System.out.println(res.size());

        for (List l : res) {
            System.out.println(l.toString());
            for(Object str:l){
                System.out.println(str);
            }
            System.out.println("-------------------");
        }
    }


    public List<List<String>> solveNQueens(int n) {
        List<List<String>> res = new ArrayList<List<String>>();
        String[] queens = new String[n];

        // 每一行用n个'.'填充
        char[] initial = new char[n];
        Arrays.fill(initial, '.');

        // n*n的棋盘用n行'.'填充
        Arrays.fill(queens, String.valueOf(Arrays.copyOf(initial, n)));

        // 45度斜线+135度斜线+n列
        int[] flag = new int[5 * n - 2];
        Arrays.fill(flag, 1);

        backtracking(res, queens, flag, 0, n);
        return res;
    }

    private void backtracking(List<List<String>> res, String[] queens, int[] flag, int row, int n) {
        if (row == n) {
            res.add(new ArrayList<String>(Arrays.asList(queens)));
            return;
        }
        for (int col = 0; col != n; col++) {

            if (flag[col] == 1 && flag[n + col + row] == 1 && flag[4 * n - 2 + col - row] == 1) {  // 判断列和两条斜线上是否有'Q'
                flag[col] = 0;  // 该列flag设为1，说明该列已经有Q了

                flag[n + col + row] = 0; // 45度斜线上的flag设为0

                flag[4 * n - 2 + col - row] = 0; // 135度斜线上的flag设为0
                char[] chars = queens[row].toCharArray();

                chars[col] = 'Q';
                queens[row] = String.valueOf(chars);

                backtracking(res, queens, flag, row + 1, n);

                chars = queens[row].toCharArray();
                chars[col] = '.';
                queens[row] = String.valueOf(chars);

                flag[col] = 1;
                flag[n + col + row] = 1;
                flag[4 * n - 2 + col - row] = 1;
            }
        }
    }
}

　　运行结果：

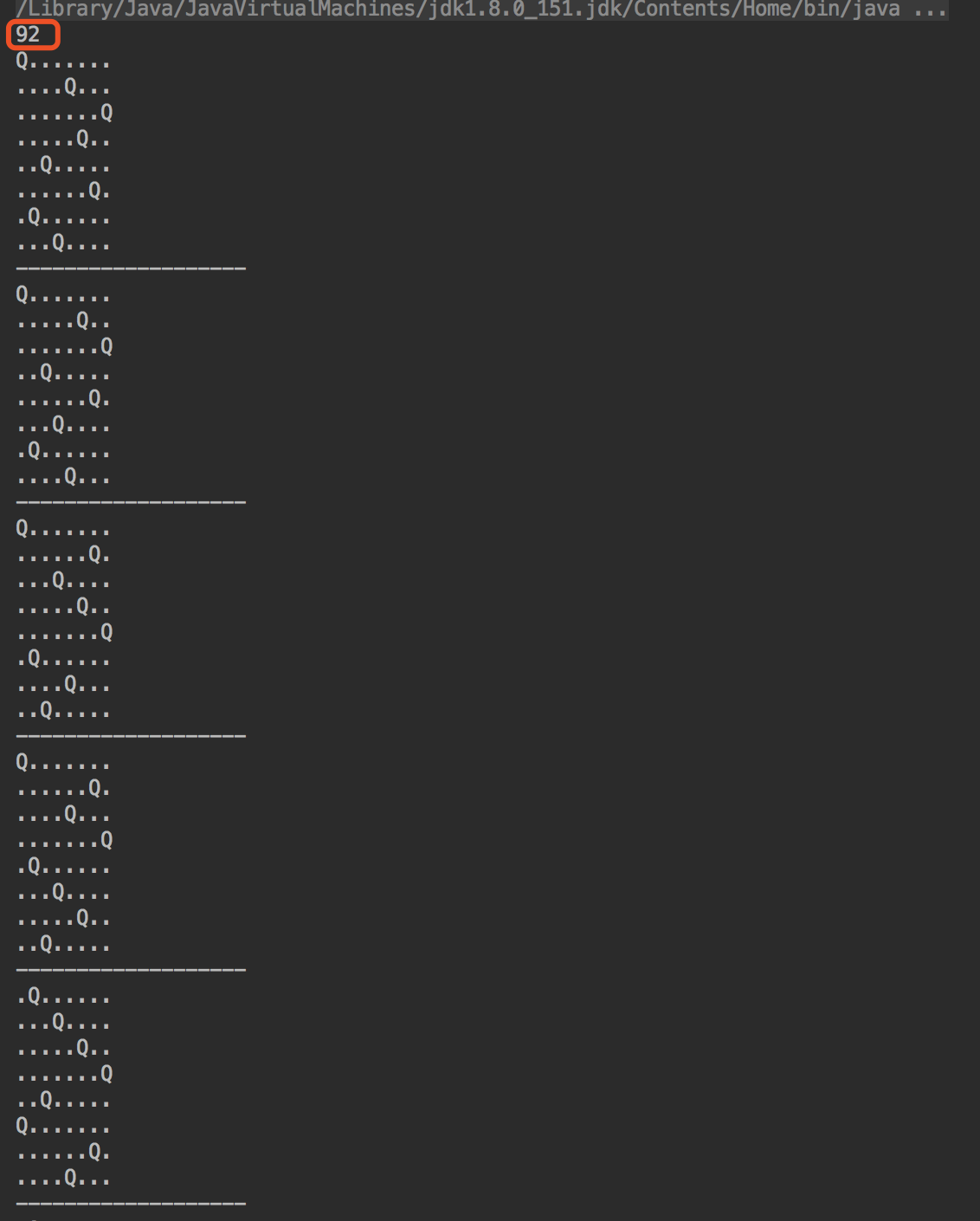
 一共有92中排列方式