slope trick
P4597 序列 sequence
首先考虑 \(dp\) 。
由于只需将序列改为非严格递增,那么就有一个贪心,即最终答案的数集不会变大。
为什么呢?
这是因为只有序列某一位置严格递减时,才会进行修改。
修改可以将前面的数降到和后面的数一样大,或者将后面的数提到和前面的数一样大。
而这样只会让数集变小或不变。
那么设 \(f[i][j]\) 表示将第 \(i\) 个数变为 \(a[j]\) 并使序列非严格递增的最小代价。
\(f[i][j]=\min(f[i-1][k]+|a_i-a_k|)\)
时间复杂度 \(O(n^2)\)。
无法通过此题。
为了方便理解,将 \(dp\) 数组拆为两个来看。
\(f[i][j]\) 表示前 \(i\) 个数,将第 \(i\) 个数改为 \(\le j\) 并使序列非严格递增的最小代价。
\(g[i][j]\) 表示前 \(i\) 个数,将第 \(i\) 个数改为 \(j\) 并使序列非严格递增的最小代价。
\(g[i][j]=f[i-1][j]+|a_i-j|\)
\(f[i][j]=\min_{k\le j}(g[i][k])\)
每次固定 \(i\) ,以 \(j\) 为横坐标,函数值为纵坐标,构建平面直角坐标系。
设 \(G_i\) 表示当 \(i\) 确定后的 \(g\) 函数图像, \(F_i\) 表示当 \(i\) 确定后的 \(f\) 函数图像。
\(G_1\):

\(F_1\):

\(G_2\) 可由 \(F_1\) 转移而来,即在 \(F_1\) 上加一个绝对值函数。


那么 \(F_2\) 就是

或者 \(G_2\) 是


那么 \(F_2\) 就是

可以发现,\(F_i\) 是一个斜率递增,公差为 \(1\) ,最后一段与 \(x\) 轴平行的凸函数,\(G_2\) 是一个斜率单调递增,最后一段斜率为 \(1\) 的凸函数。
而答案就是 \(G_n/F_n\) 最低点距离 \(x\) 轴的距离。
那么如何维护这两个下凸函数呢?
首先考虑计算答案时需要什么。
可以发现只有 \(a_i\) 比当前决策点小时答案会更新。
从绝对值函数的转折点开始考虑。
转折点处的函数值一定不变,因为转折点的纵坐标为 \(0\)。
转折点前的所有函数斜率 \(-1\) ,但决策点横坐标不变。
转折点后的所有函数斜率 \(+1\) ,决策点横坐标同样不变。
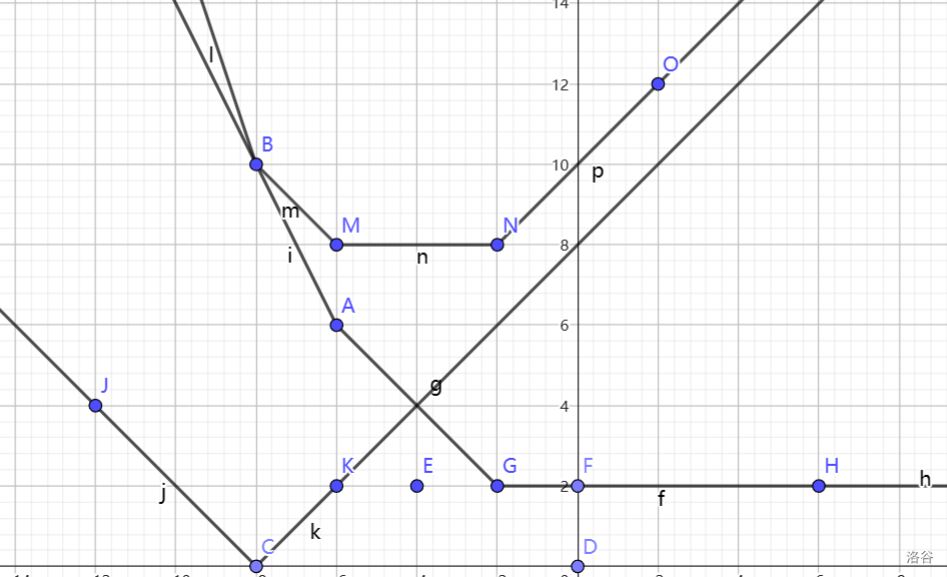
原函数为 \(BAGF\),加上了函数 \(JCK\),变成了函数 \(BMNO\)
那么对答案的贡献即为 \(M\) 与 \(G\) 的纵坐标之差。
而纵坐标之差可以分为 \(MA\) 与 \(NG-MA\) 来求。
由于 \(BM\) 与 \(BA\) 的斜率差为 \(1\) ,所以横坐标之差等于纵坐标之差。
由于 \(MN\) 与 \(AG\) 的斜率差为 \(1\) ,所以横坐标之差等于将 \(MN\) 向下平移到 \(A\) 时的 \(NG\) 长度。
这样全部加起来,答案就是新决策点与原决策点的纵坐标之差。
所以我们需要知道所有的 \(\leq0\) 的斜率来维护每次决策点的更新,并计算答案。
如何维护?
首先看 \(a_i\) 在原决策点右侧或原决策点位置的情况。
那就是左侧所有函数的斜率 \(-1\) ,右侧最终取完 \(\min\) 后斜率还是 \(0\)。
所以可以想到维护一个优先队列,每次插入 \(a_i\) 表示有一条与 \(x\) 轴平行的横坐标从 \(a_i\) 到 \(+\infty\) 的射线。
那么优先队列中的斜率是什么呢?
可以发现,此时优先队列中点的斜率就是其在优先队列中排名 \(-1\) 的相反数。
但是,如果相邻两个点间的斜率差 \(>1\) ,怎么表示?
那就插入一个点多次。
现在,优先队列中的斜率就变成了与当前点数值相等的最左侧的点在优先队列中的排名-1的相反数。
如果 \(a_i\) 在原决策点左侧,又该如何维护优先队列呢?
对原函数的改动还是将 \(a_i\) 左侧的函数斜率 \(+1\),右侧的函数斜率 \(-1\)。
相当于在 \(a_i\) 位置插入两个线段,因为当前位置斜率改变了 \(2\)。
就完了。
P4331
严格递增,并要求输出方案。
对于严格递增,只需要先将 \(a_i-i\) ,最后再加回去即可转化为非严格递增。
如何输出方案?
先给出结论:每一项先取 \(q.top\) ,最后做一遍后缀 \(\min\) 即可。
首先对于最后一项,取 \(q.top\) 一定存在一种最优方案。
对于前一项,如果比后一项大,不妨将其变的和后一项一样大,这样是保证最优的。
因为每个点取的都是 \(q.top\) ,而这是每个点最小的最优可能值。
如果比后一项小,那么对于这一项到第一项,以当前项的 \(q.top\) 为结尾一定是最优的。
所以每次记录下来 \(q.top\) ,最后做一遍后缀 \(\min\)即可。
ABC250G
懒得细写了,说说 slope trick 部分自己觉得比较重要的东西。
首先操作是将原函数、原函数平移 \((-1,w_i)\)、原函数平移 \((1,-w_i)\) 取 \(\max\)。
这使得我们无法像之前那样维护拐点,因为拐点在平移;而我们也不能打标记,因为只有部分拐点平移。
但是,可以发现每次只会在横坐标移动 \(1\),所以可以维护每个单位长度内的斜率。
每次平移后可能且仅可能产生一个新的斜率,并且它的斜率就是移动的斜率。
这个手玩一下,分类讨论。
然后怎么算答案?
答案就是 \(F_n\) 图像中与 \(y\) 轴的交点的纵坐标。
发现最低点的函数值是特殊的,我们可以直接算出。
再根据所维护的斜率倒推出答案即可。
写的有点草率了,但是如果你能从头看到这里并且把前面都看懂,相信你一定能搞明白的。
ARC070E
slope trick 的另一种技巧:打标记。
操作是左边部分整体向左平移,右边部分整体向右平移,插入绝对值函数。
用两个优先队列对左右两边分别维护。
这次是整体平移,就可以打标记了。
优先队列中维护的是相对于一开始的值不变的位置,而实际位置需要算上标记,向优先队列中插入时也需算上标记。
注意加绝对值函数时可能会将优先队列中的点放入另一个优先队列中。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号