Floyd算法和Dijkstra算法---解点到点最短路径问题

Floyd算法和Dijkstra算法

 

Floyd算法

 

检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，设置Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离。

具体计算方式借鉴https://www.cnblogs.com/ECJTUACM-873284962/p/6995648.html  中的十字交叉法

 

 

 

 

 

 

 

 

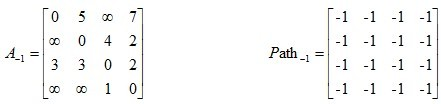
 具体代码在https://github.com/hubowen1/-

 

 

Dijkstra算法

 

 

1）寻找未被遍历的节点中权值最下的节点

2）将寻找到的最小权值节点更新为已被遍历，在运筹学中记录为被固定标号，其余为临时性标号

3）更新权值，算法将起始的节点定位于当前寻找到的最小权值节点处

 

 

 

 

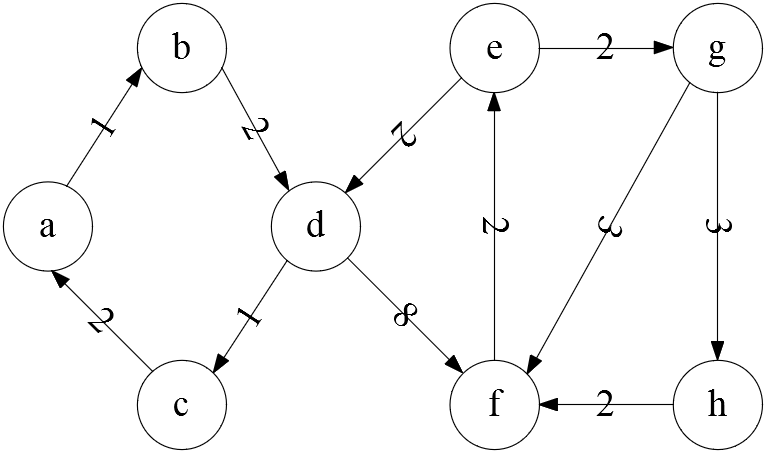
按照题目要求录入数组中

int adj_arr[N][N] = {{0, 1, INF, INF, INF, INF, INF, INF},
{INF, 0, INF, 2, INF, INF, INF, INF},
{2, INF, 0, INF, INF, INF, INF, INF},
{INF, INF, 1, 0, INF, 8, INF, INF},
{INF, INF, INF, 2, 0, INF, 2, INF},
{INF, INF, INF, INF, 2, 0,INF,INF},
{INF, INF, INF, INF, INF, 3, 0, 3},
{INF, INF, INF, INF, INF, 2, INF, 0}};

 

 

其核心为：

void shortest_path(int start, int end){ // 基于Dijkstra算法的最短路径函数
int distance[N]; // 用于存放起始点到其余各点的最短距离
int path[N]; // 用于存放起始点到其余各点最短路径的前一个顶点
int used[N] = { 0 }; // 用于标记该顶点是否已经找到最短路径
int i, j, min_node, min_dis, pass_flag = 0;
for(i = 0; i < N; i++){
distance[i] = adj_arr[start][i]; // 初始化距离数组
if(adj_arr[start][i] < INF){
path[i] = start; // 初始化路径数组
}else{
path[i] = -1;
}
}
used[start] = 1;
path[start] = start;
for(i = 0; i < N; i++){
min_dis = INF;
for(j = 0; j < N; j++){
if(used[j] == 0 && distance[j] < min_dis){
min_node = j;
min_dis = distance[j];
pass_flag++; // 标记是否存在通路
}
}
if(pass_flag != 0){
used[min_node] = 1;
for(j = 0; j < N; j++){
if(used[j] == 0){
if(adj_arr[min_node][j] < INF && distance[min_node] + adj_arr[min_node][j] < distance[j]){
distance[j] = distance[min_node] + adj_arr[min_node][j];
path[j] = min_node;
}
}
}
}else{
printf("There is no path!\n");
return;
}
}
print_shortest_path(distance, path, used, start, end);
return;
}