数据结构

并查集

例1

有 $n$ 个变量 ，可以加入若干个关系限制：

$1\;i\;j $：加入 $a_i=a_j$的条件

$2\;i\;j $：加入 $a_i\not=a_j$的条件

加完之后判断合不合法。

分为 $i$ 和 $i+n$ 两种点

操作1，连 $i,j$ 和 $i+n,j+n$

操作2，连 $i,j+n$ 和 $i+n,j$

最后判 $i,i+n$ 是否在同一集合即可

例2

给定一棵 $n$ 个点的树，支持以下操作：

1 u v 在 和 之间加一条边。允许重边，没有自环。
2 u v 询问 两个点是否在某个边不相交的环上。

操作1，每次把 $u$ 到 $v$ 的简单路径覆盖

操作2，查询 $u$ 到 $v$ 之间的简单路径是否全部覆盖

并查集暴力合并即可（最多$n$次）

可撤销并查集

按秩合并，记录上一次操作

ST表

例1

有长度为 $n$ 的十进制大数 $s_{1...n}$

有$m$个限制条件形如 $s[l_1,r_1]=s[l_2,r_2](r_1-l_1=r_2-l_2)$

问满足条件的数有多少个$(n,m<=1e5)$

记 $f_{i,j}$ 表示区间$[i,i+2^j-1]$ 的并查集

两个并查集的$merge$相当于这两段区间对应的元素相同

对于每次操作，把操作区间拆成二进制形式

对应区间$merge$一下

最后统计时，从大到小枚举$j$，将标记下放，即$merge(f_{i,j-1},f_{i',j-1})$ 和 $merge(f_{i+2^{j-1},j-1},f_{i'+2^{j-1},j-1})$

最后看有多少种相同的元素即可

Kruskal 重构树

没啥例题

树状数组

树状数组二分

从二进制高位枚举，利用树状数组性质，看取了某一位后是否依然满足条件，最后的数即为答案

以寻找第一个前缀和 $>=x$ 的位置为例

for(int j=20;j;j--){
    if(c[i+(1<<j)]<=s) i+=(1<<j),s-=c[i+(1<<j)];
}

例1

有两个二元组集合 $A,B$。有 $q$ 次操作形如：

在 $A$ 中插入 / 删除一个二元组。

在 $B$ 中插入 / 删除一个二元组。

每次操作后，求$max_t (min (∑_{(x,y)∈A} [x ≤ t]y,∑_{(x,y)∈B} [x ≥ t]y ))$

$q ≤ 2 × 10^ 6 , x ≤ 2 × 10^ 9 , ∑ y ≤ 2 × 10^ 9$

把$min$里面那两坨东西变成两个表达式

发现一个单调不递减，一个单调不递增

那求的$max$即为两个函数的交点

开始第二个函数的值大于第一个函数的值

那要找的就是第一个第二个函数小于第一个函数的位置

用树状数组二分求解

线段树

例1、矩形面积并

扫描线+线段树

从下往上扫，每一层的贡献为 被覆盖次数$>=1$的长度$\times$当前这一层的宽度

每一层的覆盖用线段树实现

区间加，记录区间最小值，区间最小值个数

最小值为$0$时，要求的长度为总长度减去最小值个数

反之，为总长度

例2

高速公路

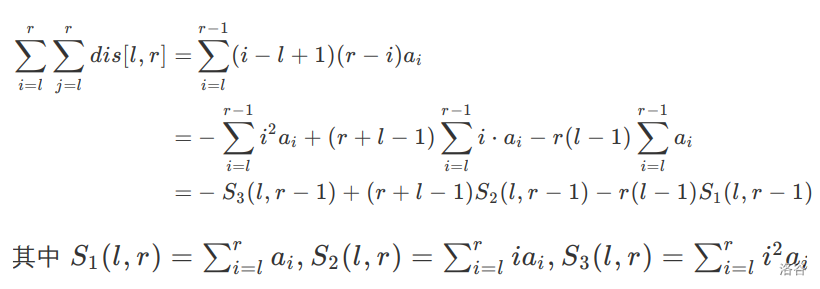
三个线段树维护即可

例3

区间加斐波那契数列

支持区间加（第一项开始的斐波那契），询问区间和

$n,m<=3*10^5$

斐波那契额数列通向式

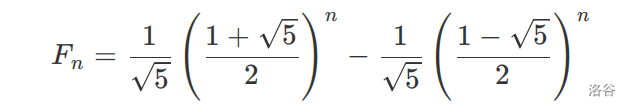
问题可以转化成区间加等比数列（分成两部分）

标记下放直接把第一个数加起来就行

对于 $\sqrt5$ 其对于此模数的二次剩余为 $383008016$

线段树即可

例4

$n$的排列 $A$，问是否存在 $x,y,z$ 使得 $A_x,A_y,A_z$构成等差数列

先枚举 $y$

对每个$x<=y$，$c[A_x]=1$

对每个$z>=y$，$c[A_z]=0$

如果有等差数列，那么说明$\exists t,c[A_y-t]\not=c[A_y+t]$

如果没有，说明$\forall t,c[A_y-t]=c[A_y+t]$

那就是判断以$y$为中心的最大串是否为回文串

利用线段树维护即可（分别记录正串反串的值）

例5

一个$n*n $的黑白棋盘，每次把$(x,y)$颜色取反，每次操作后输出黑白联通快个数

$n<=100,Q<=10^4$

建一个线段树，每一行为一个节点，节点记录每一行的并查集

单点修改暴力重建并查集，向上合并

合并时，看相邻两行上下节点的颜色是否相同，相同就merge

例6

平面上有$n$个点 $(x_i,y_i)$，权值为$c_i$ 。你需要画一个方形，使得方形的对角线在 $y=x$上。你获得的价值是方形匡住的点（边界也算）的权值和减去方形的边长。求最大价值。

$n,x_i,y_i<=5*10^5$

先将所有点对称到$y=x$上方

跑扫描线，从下往上

记$a_i$表示对于当前扫描线，$x=i$时的价值

那每层的价值就是$max\;a_i$

考虑$y\rightarrow y+1$ 如何修改

首先把上面点插入，区间加

然后减去增加的正方形边长，区间减

线段树即可

例7

给定数列，区间查询和，区间取模，单点修改。

$a\;mod\;x=a\;(x>a)$

$a\;mod\;x<=a/2\;(x<=a)$

暴力取模，每个数最多取模$logV$次

$O(mlognlogV)$

例8

给定数列，支持区间加，区间$gcd$

利用差分

区间加就是单点加

$gcd(a, b, c, d, ...) = gcd(a, b - a, c - b, d - c, ...)$

用线段树维护即可

线段树合并

从两颗线段树的根开始，同步遍历两个儿子

若一个为空，则返回另一个

李超线段树

标记永久化，依次递归上来就行

例9

题面：T11

考虑没有删除的情况

扫描线

枚举$i$，表示正在处理第$i$个序列

定义$a[j]$表示第j个时刻插入了多少个数

$b[j]$表示j时刻插入的数是多少

对于查询操作

如果$a_1+a_2+...+a_t<b$ 输出0

否则就要找出最小的$k$使得

$a_1+a_2+...+a_k>=b$

树状数组二分可以解决

接着解决扫描线向上扫的过程

当$i\rightarrow i+1$时

把所有右端点为$i$的操作（假设时刻为t）进行删除

即$a[t]-=k,b[t]=0$

把所有左端点为$i+1$的操作（假设时刻为t）加入

即$a[t]+=k,b[t]=c$

考虑有删除的情况

发现删除只对查询有影响

删去k个数，就可以看做查询时，查询第$b+k$个数

但删除是如果序列长度不足k，只需将整个序列删除

那我们就要统计在每次查询之前，这个序列走了几个人

这个值等价于，忽略删除时序列总人数$-$不忽略时序列总人数

分别用一颗线段树求值

按输入顺序进行操作

忽略的部分直接加，碰到查询记录一共多少人

不忽略的话碰到删除操作，直接减，再对$0$取$max$