专题二 MATLAB矩阵处理 2.1特殊矩阵

专题二 MATLAB矩阵处理

2.1特殊矩阵

• 通用性的特殊矩阵
• 用于专门学科的特殊矩阵

通用的特殊矩阵

• zeros函数： 产生0矩阵,即零矩阵
• ones函数： 产生全1矩阵,即幺矩阵
• eye函数: 产生对角线为1的矩阵。当矩阵是方阵时,得到一个单位矩阵。
• rand函数: 产生(0,1)区间均匀分布的随机矩阵。
• randn函数: 产生均值为0，方差为1的标准正态分布随机矩阵

zeros函数的调用格式:

• zeros(m):产生m乘m零矩阵

• zeros(m,n): 产生m×n零矩阵

• zeros(size(A))：产生与矩阵A同样大小的零矩阵

  

用于专门学科的特殊矩阵

1. 魔方矩阵

   

   • n阶魔方阵由1，2，3，...,n^2共n2个整数组成,且每行每列以及主、副对角线上各n各元素之和都相等。
   • n阶魔方阵每行每列元素的和为(1+2+3+...+n^2)/n=(n+n3)/2。
   • matlab函数magic(n)产生一个特定的魔方阵。

2. 范德蒙矩阵

   

   在MATLAB中,函数vander(V)生成以向量V为基础的范德蒙矩阵

   

   范德蒙矩阵常用在各种通信系统的纠错编码中。

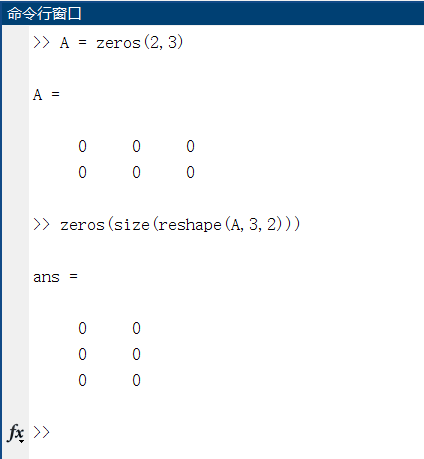
3. 希尔伯特矩阵

   

   在MATLAB中,生成n阶希尔伯特矩阵的函数是hilb(n).

   

4. 伴随矩阵

MATLAB生成伴随矩阵的函数时compan(p),其中p是一个多项式的系数向量,高次幂系数排在前，低次幂系数排在后。

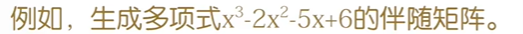
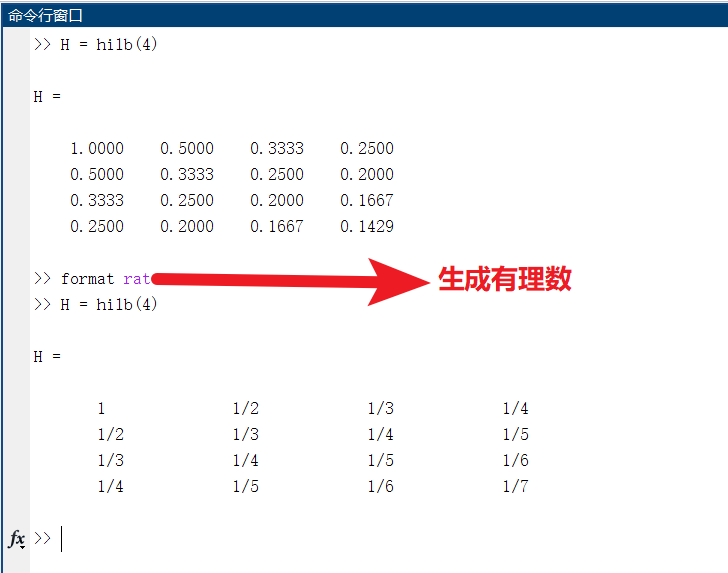
5. 帕斯卡矩阵